人教版八(上) 第十四章 全等三角形 单元测试培优卷
试卷更新日期:2025-09-30 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 如图,DE⊥AC , BF⊥AC , 垂足分别是E , F , 且DE=BF , 若利用“HL”证明△DEC=△BFA , 则需添加的条件是( )
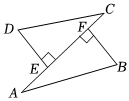 A、EC=FA B、DC=BA C、∠D=∠B D、∠DCE=∠BAF2. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( )
A、EC=FA B、DC=BA C、∠D=∠B D、∠DCE=∠BAF2. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( ) A、SSS B、SAS C、AAS D、ASA3. 如图, △ABC≌△DEF,若∠B=125°, ∠F=35°,则∠A的度数为( )
A、SSS B、SAS C、AAS D、ASA3. 如图, △ABC≌△DEF,若∠B=125°, ∠F=35°,则∠A的度数为( )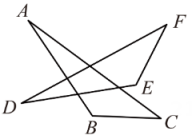 A、35° B、30 C、25° D、20°4. 如图,点 在 上, ,若 ,则 的长度为( )
A、35° B、30 C、25° D、20°4. 如图,点 在 上, ,若 ,则 的长度为( )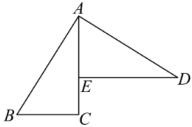 A、1
A、1
B、2
C、3
D、4
5. 在2×3网格中,三角形的顶点在格点上,求α+β的值( ) A、45° B、90° C、100° D、不确定6. 如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路(AB,AC,BC) 的距离都相等,则油库的位置可以设计在( )
A、45° B、90° C、100° D、不确定6. 如图,三条公路两两相交,现计划修建一个油库,要求油库到这三条公路(AB,AC,BC) 的距离都相等,则油库的位置可以设计在( ) A、△ABC三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条边的垂直平分线的交点7. 如图,在中, , 平分交于点D, , 垂足为E,的面积为5,则的长为( )
A、△ABC三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条边的垂直平分线的交点7. 如图,在中, , 平分交于点D, , 垂足为E,的面积为5,则的长为( )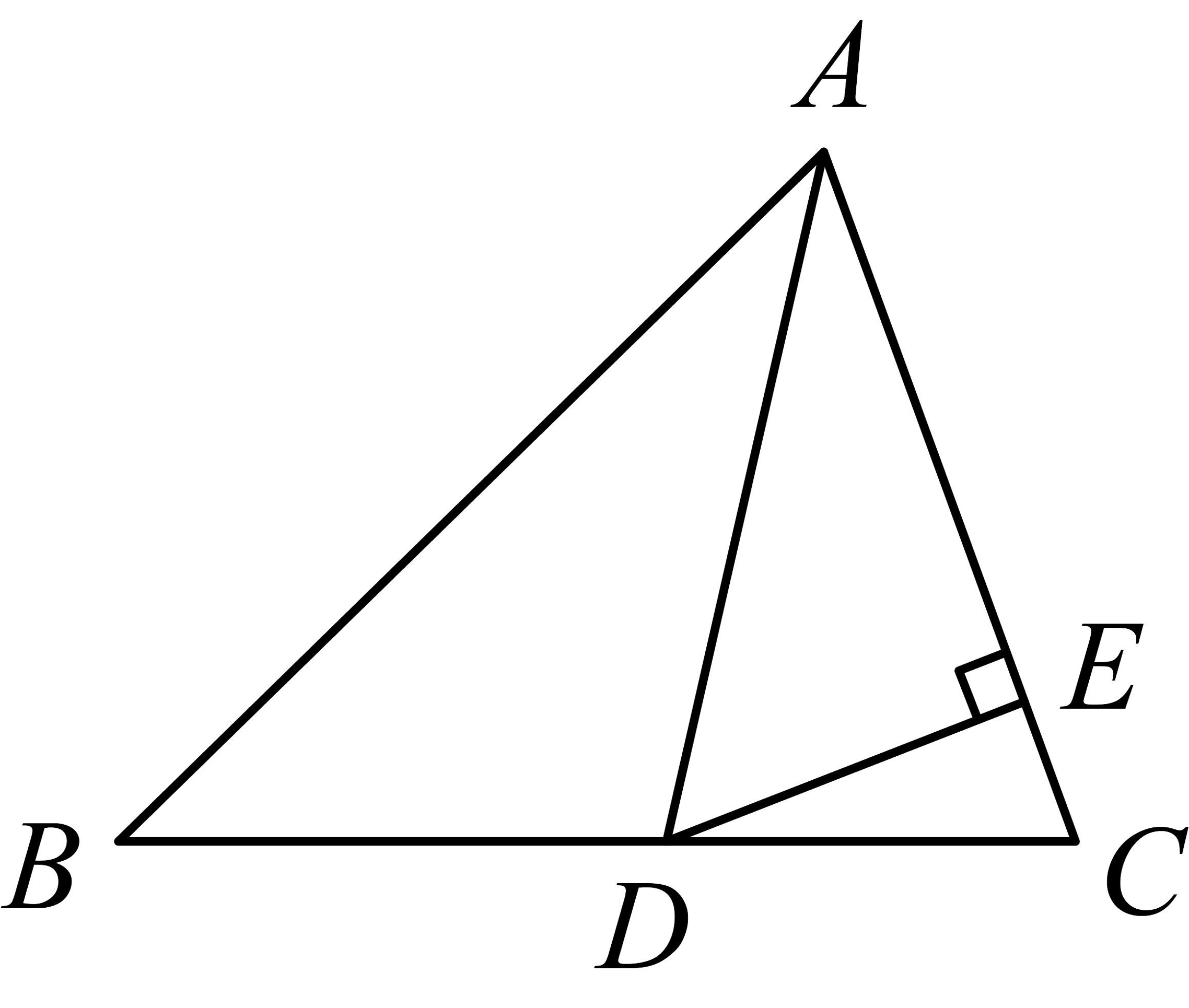 A、1 B、2 C、3 D、58. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )
A、1 B、2 C、3 D、58. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )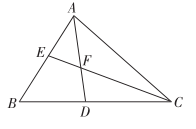
①;②;③若 , 则;④ .
A、1个 B、2个 C、3个 D、4个9. 如图,在△ABC中,∠ACB=60°,AG平分∠BAC交BC与点G , BD平分∠ABC交AC于点D , AG、BD相交于点F , BE⊥AG交AG的延长线于点E , 连接CE , 下列结论中正确的是( )
①若∠BAD=70°,则∠EBC=5°;②BF=2EF;③BE=CE;④AB=BG+AD .
A、4个 B、3个 C、2个 D、1个10. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( ) A、① B、①② C、①②③ D、①②④
A、① B、①② C、①②③ D、①②④二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 如图,在中,平分 , , 的面积为45,的面积为20,则的面积等于 .
 12. 如图,在中, , M、N、K分别是 , , 上的点,且 , . 若 , 则的度数为 .
12. 如图,在中, , M、N、K分别是 , , 上的点,且 , . 若 , 则的度数为 .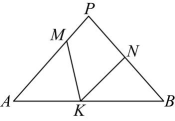 13. 如图,在中, , 以点B为圆心,适当长为半径作弧,分别交 , 于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知 , , 则的长为 .
13. 如图,在中, , 以点B为圆心,适当长为半径作弧,分别交 , 于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知 , , 则的长为 . 14. 如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= .
14. 如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= .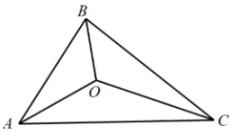 15. 如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .
15. 如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .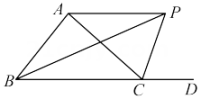
三、解答题:本大题共8小题,共75分.
-
16. 如图和中, , 点在同一直线上,有如下三个关系式: .
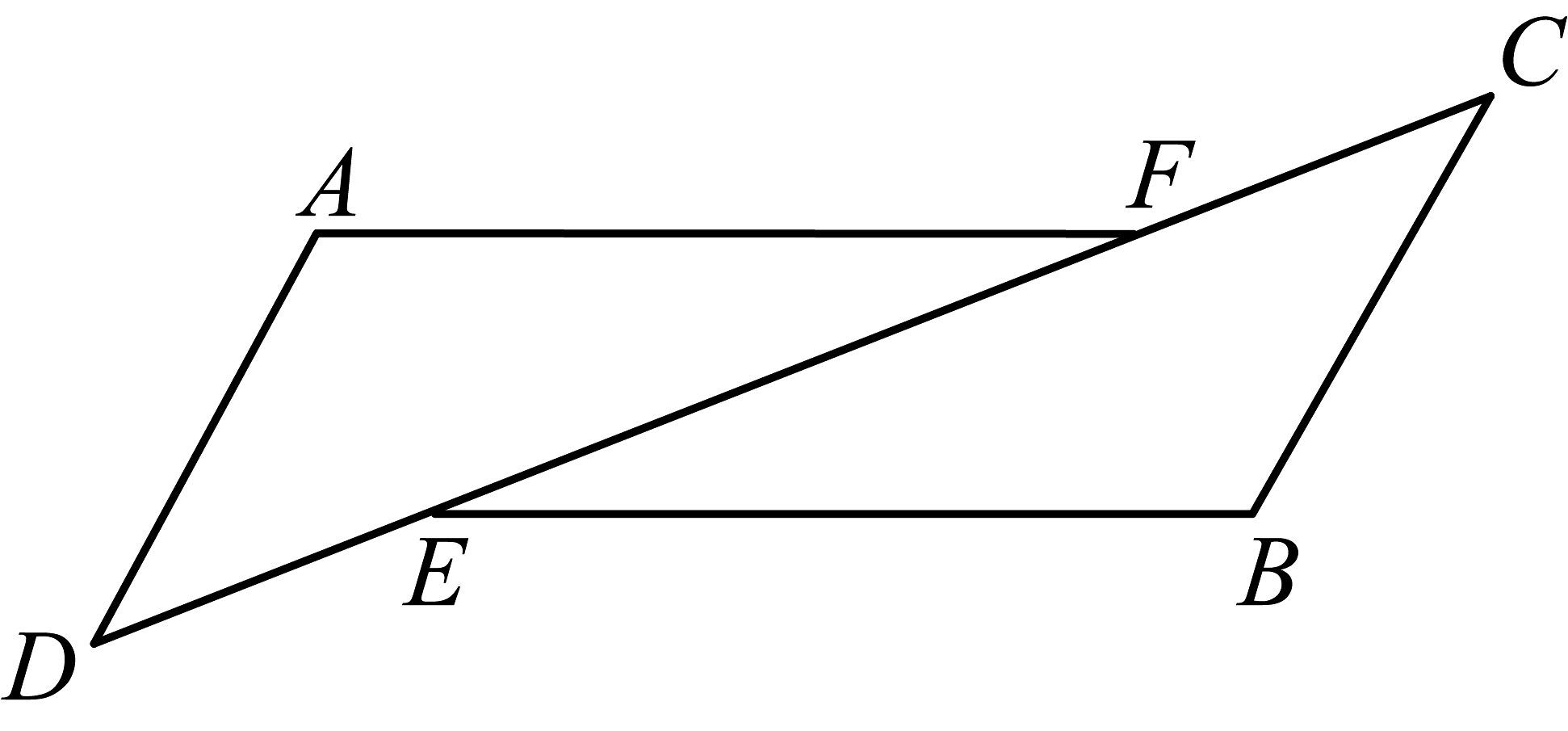 (1)、请用其中两个关系式作为条件,另一个作为结论,写出所有正确的命题(用序号写出命题书写形式,即写成如果……,那么……形式.);(2)、选取(1)中一个正确的命题进行证明.17. 如图,在△ABC中,点D是AC上一点,AD=AB,过点D作DE∥AB,且DE=AC.
(1)、请用其中两个关系式作为条件,另一个作为结论,写出所有正确的命题(用序号写出命题书写形式,即写成如果……,那么……形式.);(2)、选取(1)中一个正确的命题进行证明.17. 如图,在△ABC中,点D是AC上一点,AD=AB,过点D作DE∥AB,且DE=AC. (1)、求证:∠ACB=∠AED.(2)、若点D是AC的中点,且S△ABC=12,求四边形ABCE的面积.18. 如图,△ABD≌△CAE,点A,D,E三点在一条直线上.
(1)、求证:∠ACB=∠AED.(2)、若点D是AC的中点,且S△ABC=12,求四边形ABCE的面积.18. 如图,△ABD≌△CAE,点A,D,E三点在一条直线上. (1)、求证:BD=CE+DE;(2)、当△ABD满足什么条件时,BD∥CE? 请说明理由.19. 如图,在中,D为上一点,E为中点,连接并延长至点F,使得 , 连 .
(1)、求证:BD=CE+DE;(2)、当△ABD满足什么条件时,BD∥CE? 请说明理由.19. 如图,在中,D为上一点,E为中点,连接并延长至点F,使得 , 连 . (1)、求证:(2)、若 , 求的度数.20. 如图,在直角坐标系中,点 , 点B为x轴正半轴上一个动点,以为边作 , 使 , 且点C在第一象限内.
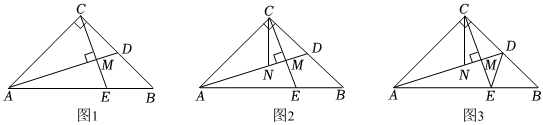
(1)、求证:(2)、若 , 求的度数.20. 如图,在直角坐标系中,点 , 点B为x轴正半轴上一个动点,以为边作 , 使 , 且点C在第一象限内.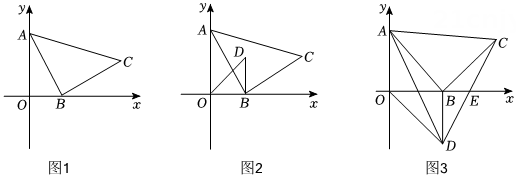 (1)、如图1,若 , 求点C的坐标.(2)、如图2,过点B向x轴上方作 , 且 , 在点B的运动过程中,探究点C,D之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)、如图3,过点B向x轴下方作 , 且 , 连结交x轴于点E,当的面积是的面积的2倍时,求的长.21. 观察、猜想、探究:
(1)、如图1,若 , 求点C的坐标.(2)、如图2,过点B向x轴上方作 , 且 , 在点B的运动过程中,探究点C,D之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)、如图3,过点B向x轴下方作 , 且 , 连结交x轴于点E,当的面积是的面积的2倍时,求的长.21. 观察、猜想、探究:在△ABC中,∠ACB=2∠B.
(1)如图①,当∠C=90°,AD为∠BAC的角平分线时,过D作AB的垂线DE,垂足为E,可以发现AB、AC、CD存在的数量关系是 ;
(2)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD是否还存(1)中的数量关系?如果存在,请给出证明.如果不存在,请说明理由;
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.