人教版九(上)数学第二十一章 一元二次方程 单元测试培优卷
试卷更新日期:2025-09-30 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 把方程化成的形式,则( )A、17 B、14 C、11 D、72. 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 在我国古代数学名著《算法统宗》里有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和身高为5尺的人一样高,秋千的绳索始终是拉直的,试问绳索有多长?”设绳索长为x尺,则x满足的方程为( )
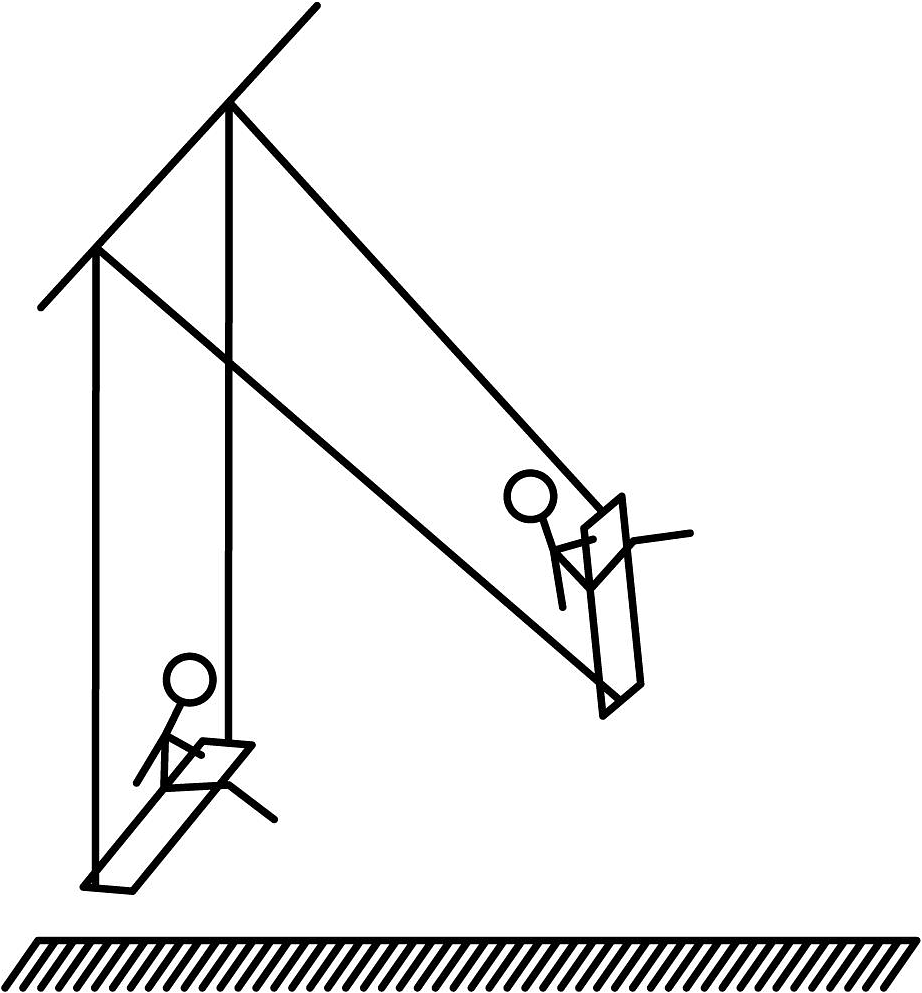 A、x2=102+(x-5-1)2 B、x2=(x﹣5)2+102 C、x2=102+(x+1-5)2 D、x2=(x+1)2+1024. 若α,β是方程x2﹣2x﹣3=0的两个实数根,则α2+β2的值为( )A、10 B、9 C、7 D、55. 某经济技术开发区今年一月份工业产值达50亿元,且一月份、二月份、三月份的总产值为亿元,若设平均每月的增长率为 , 根据题意可列方程( )A、 B、 C、 D、6. 已知关于的一元二次方程有实数根,则的取值范围为( )A、 B、 C、 D、7. 如图,在长为 , 宽为的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是 , 则小路的宽是( )
A、x2=102+(x-5-1)2 B、x2=(x﹣5)2+102 C、x2=102+(x+1-5)2 D、x2=(x+1)2+1024. 若α,β是方程x2﹣2x﹣3=0的两个实数根,则α2+β2的值为( )A、10 B、9 C、7 D、55. 某经济技术开发区今年一月份工业产值达50亿元,且一月份、二月份、三月份的总产值为亿元,若设平均每月的增长率为 , 根据题意可列方程( )A、 B、 C、 D、6. 已知关于的一元二次方程有实数根,则的取值范围为( )A、 B、 C、 D、7. 如图,在长为 , 宽为的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是 , 则小路的宽是( ) A、 B、 C、或 D、8. 如图,在正方形中,E是边中点,F是边上一动点,G是延长线上一点,且 . 若 , 则的最小值为( )
A、 B、 C、或 D、8. 如图,在正方形中,E是边中点,F是边上一动点,G是延长线上一点,且 . 若 , 则的最小值为( ) A、 B、 C、 D、9. 关于x的一元二次方程在范围内有且只有一个根,则m的取值范围为( )A、 B、或 C、或 D、或10. 已知x,y为实数,且满足 ,记 的最大值为M,最小值为m,则 ( ).A、 B、 C、 D、
A、 B、 C、 D、9. 关于x的一元二次方程在范围内有且只有一个根,则m的取值范围为( )A、 B、或 C、或 D、或10. 已知x,y为实数,且满足 ,记 的最大值为M,最小值为m,则 ( ).A、 B、 C、 D、二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 一元二次方程3x(x-1)=x-1的解是.12. 已知 , 是方程的两个根,则 .13. 如图,某小区要在长为16m,宽为12m的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为m.
 14. 若是一元二次方程的两个实数根,多项式的值是 .15. 关于的一元二次方程在范围内有且只有一个根,则的取值范围为 .
14. 若是一元二次方程的两个实数根,多项式的值是 .15. 关于的一元二次方程在范围内有且只有一个根,则的取值范围为 .三、解答题:本大题共8小题,共75分.
-
16. 已知 , 是关于的方程的两个不相等的实数根.(1)、求的取值范围;(2)、若 , 且 , , 都是整数,求的值.17. 如图,老李想用长为的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈 , 并在边上留一个宽的门(建在处,另用其他材料).
 (1)、当羊圈的长和宽分别为多少米时,能围成一个面积为640的羊圈?(2)、羊圈的面积能达到吗?如果能,请你给出设计方案;如果不能,请说明理由.18. 某水果商店销售一种进价为30元/千克的优质水果,若售价为40元/千克,则一个月可售出400千克.若售价在40元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为45元/千克时,每月销售水果______千克;(2)、当每月利润为5250元时,这种水果的售价为多少?(3)、当这种水果的售价定为多少时,获得的月利润最大?最大利润是多少元?19. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)
(1)、当羊圈的长和宽分别为多少米时,能围成一个面积为640的羊圈?(2)、羊圈的面积能达到吗?如果能,请你给出设计方案;如果不能,请说明理由.18. 某水果商店销售一种进价为30元/千克的优质水果,若售价为40元/千克,则一个月可售出400千克.若售价在40元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为45元/千克时,每月销售水果______千克;(2)、当每月利润为5250元时,这种水果的售价为多少?(3)、当这种水果的售价定为多少时,获得的月利润最大?最大利润是多少元?19. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)类别
价格
A款钥匙扣
B款钥匙扣
进货价(元/件)
30
25
销售价(元/件)
45
37
(1)、网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;(2)、第一次购进的冰墩墩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?(3)、冬奥会临近结束时,网店打算把B款钥匙扣调价销售.如果按照原价销售,平均每天可售4件.经调查发现,每降价1元,平均每天可多售2件,将销售价定为每件多少元时,才能使B款钥匙扣平均每天销售利润为90元?20. 如图,平面直角坐标系中,是坐标原点,直线经过点 , 与轴交于点 , 与轴交于点 . 线段平行于轴,交直线于点 , 连接 , . (1)、填空:______,点的坐标是______;(2)、求证:四边形是平行四边形;(3)、动点从点出发,沿对角线以每秒个单位长度的速度向点运动,直到点为止;动点同时从点出发,沿对角线以每秒个单位长度的速度向点运动,直到点为止.设两个点的运动时间均为秒.
(1)、填空:______,点的坐标是______;(2)、求证:四边形是平行四边形;(3)、动点从点出发,沿对角线以每秒个单位长度的速度向点运动,直到点为止;动点同时从点出发,沿对角线以每秒个单位长度的速度向点运动,直到点为止.设两个点的运动时间均为秒.当时,求的面积;
当点 , 运动至四边形为矩形时,请求出此时的值.
21. 阅读下列材料:解方程: .
解:①当 , 即时, . 即 , 解得(不合题意,舍去),;
②当 , 即时, . 即 , 解得(不合题意,舍去),;
综上所述,原方程的解为 , .
仿照上边例题的解法,解方程: .
22. 综合与实践:九年级课外小组计划用两块长为 , 宽为的长方形硬纸板做收纳盒.
【任务要求】
任务一:设计无盖长方形收纳盒.把一块长方形硬纸板的四角剪去四个相同的小正方形,然后沿虚线折成一个无盖的长方体收纳盒.如图1.
任务二:设计有盖长方形收纳盒.把另一块长方形硬纸板的四角剪去四个相同的小长方形,然后折成一个有盖的长方体收纳盒,和两边恰好重合且无重叠部分.如图2.
【问题解决】
(1)、若任务一中设计的收纳盒的底面积为 , 剪去的小正方形的边长为多少?(2)、若任务二中设计的该收纳盒的底面积为 .①该收纳盒的高是多少?
②请判断能否把一个尺寸如图3所示的玩具机械狗完全立着放入该收纳盒,并说明理由.
23. “数形结合”是数学中的一种基本思想方法.我国著名数学家华罗庚对此曾有生动的描述:“数以形而直观,形以数而入微”.下面我们分别以我国三国时期的数学家赵爽(公元3~4世纪)和公元9世纪的阿拉伯数学家阿尔•花拉子在解一元二次方程x2+2x-35=0即x(x+2)=35时的做法为例加以说明.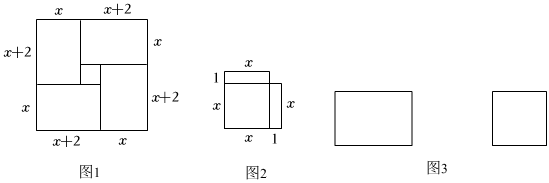
【学习研究】数学家赵爽的做法是,用四个边长分别为x , x+2且面积为x(x+2)=35的矩形构造成图1形状的大正方形,然后用两种方式表示出大正方形的面积,得到(x+2+x)2=4×35+22 , 从而得到一个正数解x=5.阿拉伯数学家阿尔•花拉子米采用的方法是用一个边长为x的正方形和2个边长分别为x , 1的矩形构造出图2的形状(面积为x2+2x=35)并把它补成一个大正方形,然后也是用两种方式表示出大正方形的面积,得到(x+1)2=(x2+2x)+12=35+1,从而得到一个正数解x=5.
(1)、图1中,小正方形的边长为 ▲ , 将图2中补充完整(补充的部分用阴影表示);(2)、【类比迁移】小明想通过以上述构造图形的方法来解一元二次方程方程x2+6x-55=0.①请分别构造以上两种图形,并在图中标注出相关线段的长;(注:第一种方法中已经画好了一个矩形,第二种方法中已经画好了一个正方形,请在已经画好的图形上进行补充)
②请分别根据所画图形,求出方程x2+6x-55=0的一个正数解.
(注:需要写出必要的推算过程)
(3)、【拓展应用】一般地,形如x2+ax=b的一元二次方程可以构造类似以上图形来求解,请选择其中的一种方法,进行图形构造,且在图中标注出相关线段的长,并直接写出该方程的正数解与负数解.