人教版九(上)数学第二十二章 二次函数 单元检测培优卷
试卷更新日期:2025-09-30 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 抛物线 的对称轴是直线( )A、 B、 C、 D、2. 已知二次函数的图象如图所示,有下列4个结论,其中正确的结论是( )
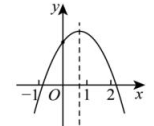 A、 B、 C、 D、3. 某湖面上有一座抛物线形拱桥,按如图所示的方式建立平面直角坐标系,得到抛物线的函数解析式为 , 正常水位时,水面宽 AB 为 16m,此时拱顶 O 到水面 AB 的距离为( )
A、 B、 C、 D、3. 某湖面上有一座抛物线形拱桥,按如图所示的方式建立平面直角坐标系,得到抛物线的函数解析式为 , 正常水位时,水面宽 AB 为 16m,此时拱顶 O 到水面 AB 的距离为( )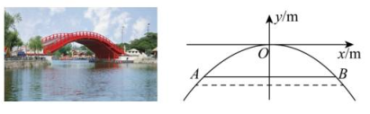 A、4m B、3m C、2m D、1m4. 已知二次函数的图象如下图所示,关于该函数在所给自变量取值范围内,下列说法中正确的是( )
A、4m B、3m C、2m D、1m4. 已知二次函数的图象如下图所示,关于该函数在所给自变量取值范围内,下列说法中正确的是( )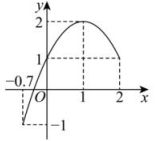 A、有最小值0,有最大值2 B、有最小值-1,有最大值0 C、有最小值-1,有最大值2 D、有最小值-1,无最大值5. 已知A(4,y1),B(1,y2),C(﹣3,y3)在函数y=﹣3(x﹣2)2+m(m为常数)的图象上,则 , , 的大小关系是( )A、 < < B、 < < C、 < < D、 < <6. 在同一坐标系中,二次函数 与一次函数 的图象可能是( )A、
A、有最小值0,有最大值2 B、有最小值-1,有最大值0 C、有最小值-1,有最大值2 D、有最小值-1,无最大值5. 已知A(4,y1),B(1,y2),C(﹣3,y3)在函数y=﹣3(x﹣2)2+m(m为常数)的图象上,则 , , 的大小关系是( )A、 < < B、 < < C、 < < D、 < <6. 在同一坐标系中,二次函数 与一次函数 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,已知二次函数的图象与轴交于点 , 与轴的交点在和之间(不包括这两点),对称轴为直线 , 下列结论:①;②;③;④;其中正确结论的个数有( )
7. 如图,已知二次函数的图象与轴交于点 , 与轴的交点在和之间(不包括这两点),对称轴为直线 , 下列结论:①;②;③;④;其中正确结论的个数有( )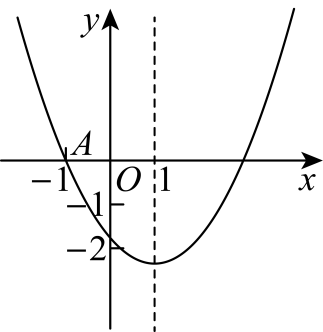 A、1个 B、2个 C、3个 D、4个8. 如图,抛物线的对称轴是 . 下列结论:①;②;③;④ , 正确的有( )
A、1个 B、2个 C、3个 D、4个8. 如图,抛物线的对称轴是 . 下列结论:①;②;③;④ , 正确的有( ) A、4个 B、3个 C、2个 D、1个9. 已知二次函数图象的一部分如图所示,该函数图象经过点 , 对称轴为直线 . 对于下列结论:①;②;③多项式可因式分解为;④当时,关于的方程无实数根.其中正确的个数有( )
A、4个 B、3个 C、2个 D、1个9. 已知二次函数图象的一部分如图所示,该函数图象经过点 , 对称轴为直线 . 对于下列结论:①;②;③多项式可因式分解为;④当时,关于的方程无实数根.其中正确的个数有( )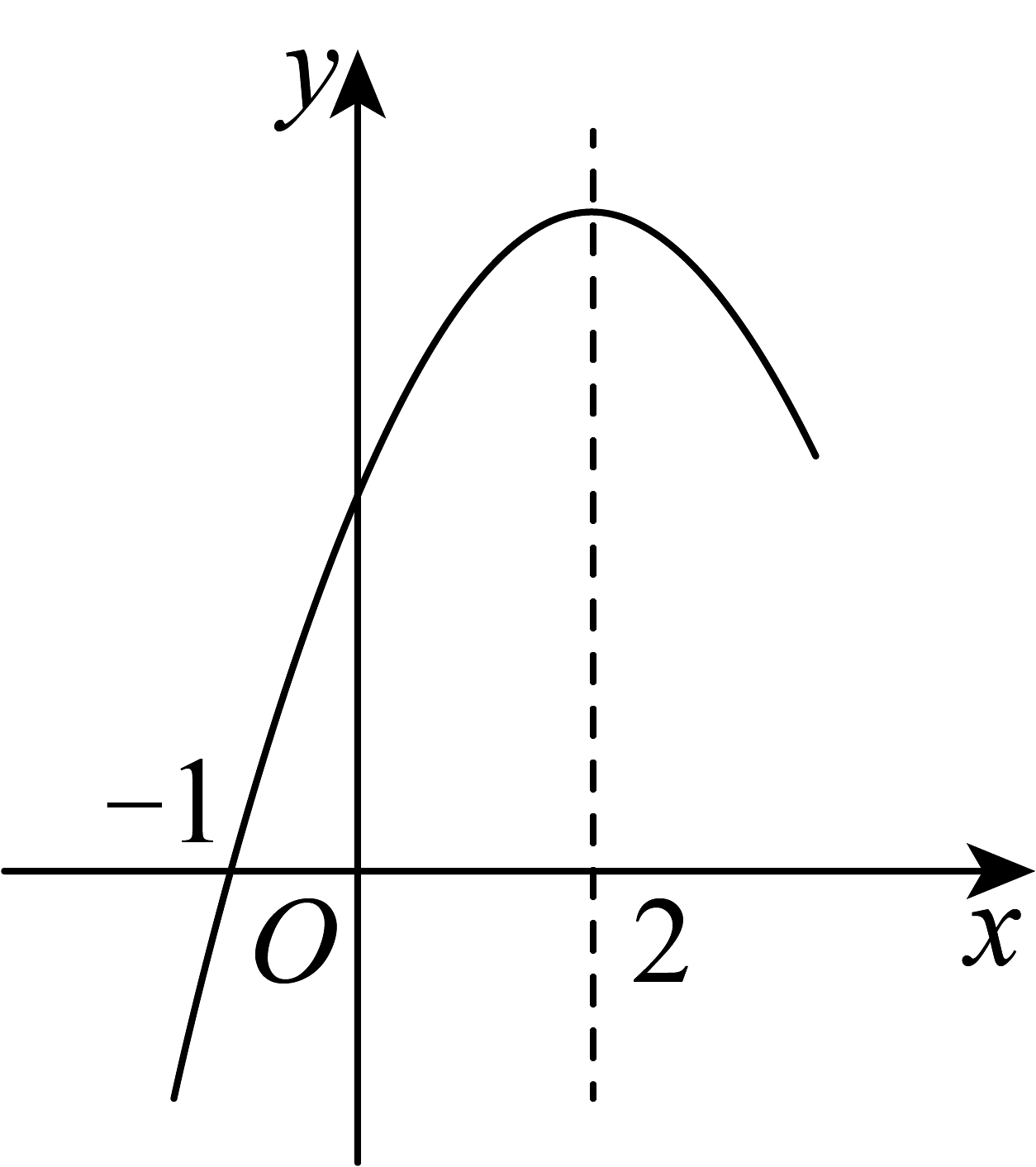 A、1个 B、2个 C、3个 D、4个10. 二次函数的图象如图所示,下列结论:①;②;③m为任意实数,则;④;⑤若 , 且 , 则 . 其中正确的个数是( )
A、1个 B、2个 C、3个 D、4个10. 二次函数的图象如图所示,下列结论:①;②;③m为任意实数,则;④;⑤若 , 且 , 则 . 其中正确的个数是( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 抛物线 与 y 轴交点的坐标为 , 与 x 轴交点的坐标为12. 二次函数 , 当 时,对于每一个 x 的值, 始终成立,则 a 的取值范围是.13. 小徐在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数 , 则小徐此次的实心球成绩为米.
 14. 已知二次函数的值恒大于0,则m的取值范围是.15. 如图,抛物线与轴交于 , 两点,顶点为 , 点为抛物线上,且位于轴下方,直线 , 与轴分别交于 , 两点,当点运动时, .
14. 已知二次函数的值恒大于0,则m的取值范围是.15. 如图,抛物线与轴交于 , 两点,顶点为 , 点为抛物线上,且位于轴下方,直线 , 与轴分别交于 , 两点,当点运动时, .
三、解答题:本大题共8小题,共75分.
-
16. 已知二次函数的图象经过点(-1, 8),(2, -1)。(1)、 求这个二次函数的解析式;(2)、 求这个图象的顶点坐标和对称轴.17. 某学校计划建一个长方形种植园,如图,种植园的一边靠墙,其余边用总长为24m的篱笆围成,已知墙a长为10m,设这个种植园垂直于墙的一边长为x(m),种植园面积为.
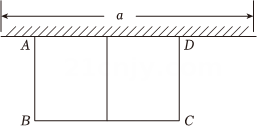 (1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、根据实际需要,要求这个种植园的面积为 , 求篱笆AB的长.18. 如图,抛物线 和直线 交于 A,B 两点.
(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、根据实际需要,要求这个种植园的面积为 , 求篱笆AB的长.18. 如图,抛物线 和直线 交于 A,B 两点.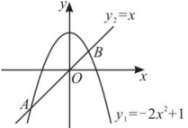 (1)、 求 A,B 两点的坐标;(2)、 根据图象,写出当 x 取何值时, .19. 已知二次函数 ( 为常数)的图象经过点 和 .
(1)、 求 A,B 两点的坐标;(2)、 根据图象,写出当 x 取何值时, .19. 已知二次函数 ( 为常数)的图象经过点 和 . (1)、求二次函数的表达式及顶点坐标;(2)、当 时,请根据图象直接写出 的取值范围.20. 根据背景素材,探索解决问题.
(1)、求二次函数的表达式及顶点坐标;(2)、当 时,请根据图象直接写出 的取值范围.20. 根据背景素材,探索解决问题.素材1
电动车是重要的出行工具之一.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.
素材2
若此种头盔的进价为30元/个,当售价为40元/个时,月销售量为600个,若在此基础上售价每涨价1元/个,则月销售量将减少10个.
问题解决
任务1
为求该品牌头盔销售量的月增长率,设增长百分率为a,依题意列方程为:________.
任务2
若该品牌头盔定价为x元/个,则销售量为________(用含x的代数式表示)
任务3
当x为多少时?销售总利润达到最大,求最大总利润.
21. 如图,正方形的边长为4,点 , 分别是边 , 上的动点(不与端点重合),且;点 , 分别是边 , 上的点, , , 设的长度为 , 四边形的面积为 .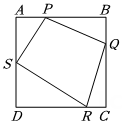 (1)、求关于的函数表达式及自变量的取值范围;(2)、四边形的面积有没有最值?如果有,请说明是最大值还是最小值,并计算此时长度,如果没有,请说明理由.22. 大棚经济“金钥匙”,激活乡村产业振兴新引擎.刘叔叔计划在自家菜地修建一个蔬菜大棚,图1是其横截面的示意图,其中 , 为两段垂直于地面的墙体,两段墙体之间的水平距离为9米,大棚的顶部用抛物线形铝合金骨架作支撑.已知骨架的一端固定在离地面3.5米的墙体处,另一端固定在墙体处,骨架最高点到墙体的水平距离为2米,且点离地面的高度为3.75米.
(1)、求关于的函数表达式及自变量的取值范围;(2)、四边形的面积有没有最值?如果有,请说明是最大值还是最小值,并计算此时长度,如果没有,请说明理由.22. 大棚经济“金钥匙”,激活乡村产业振兴新引擎.刘叔叔计划在自家菜地修建一个蔬菜大棚,图1是其横截面的示意图,其中 , 为两段垂直于地面的墙体,两段墙体之间的水平距离为9米,大棚的顶部用抛物线形铝合金骨架作支撑.已知骨架的一端固定在离地面3.5米的墙体处,另一端固定在墙体处,骨架最高点到墙体的水平距离为2米,且点离地面的高度为3.75米.请尝试数学建模解决以下问题:
 (1)、在图1中,以为原点,水平直线为轴,所在直线为轴,建立平面直角坐标系.设大棚顶部骨架上某处离地面的高度为(米),该处离墙体的水平距离为(米),求与之间的函数关系式;(2)、为了大棚顶部更加稳固,刘叔叔计划在棚顶安装铝合金支架,如图2所示,支架可以看成是由线段 , 组成,其中点 , 在顶棚抛物线形骨架上,交于点 . 为不影响耕作,将点到地面的距离定为1.5米.求做这一个支架所需铝合金材料的最大长度.23. 在学习二次函数与一元二次方程时,从二次函数图象可得如下结论.
(1)、在图1中,以为原点,水平直线为轴,所在直线为轴,建立平面直角坐标系.设大棚顶部骨架上某处离地面的高度为(米),该处离墙体的水平距离为(米),求与之间的函数关系式;(2)、为了大棚顶部更加稳固,刘叔叔计划在棚顶安装铝合金支架,如图2所示,支架可以看成是由线段 , 组成,其中点 , 在顶棚抛物线形骨架上,交于点 . 为不影响耕作,将点到地面的距离定为1.5米.求做这一个支架所需铝合金材料的最大长度.23. 在学习二次函数与一元二次方程时,从二次函数图象可得如下结论.如果抛物线与x轴有公共点的横坐标是 , 那么当x=时,函数值是0,因此是方程的一个根.
同学们,请你结合所学的数学知识解决下列问题
(1)、若二次函数(m为常数)与x轴两交点的横坐标为 , , , 求二次函数的解析式;(2)、不论 m为何值,该函数的图象都会经过一个定点,求定点的坐标;(3)、在(1)的条件下,当 , 时,对应的函数值为N,Q,若求证: