人教版数学七年级上学期重难点复习5 ：探索规律与综合实践

试卷更新日期：2025-09-28 类型：复习试卷

进入出卷网下载

一、线段、射线、直线中的规律

1. 如图是由若干个小平行四边形拼成的图形，图中共有平行四边形的个数是（）

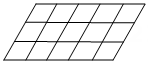A、36 B、45 C、72 D、90

查看试题解析
2. 如图，点M在线段AN的延长线上，且线段MN=20，第一次操作：分别取线段AM和AN的中点 $M_{1} ， N_{1}$ ；第二次操作：分别取线段 $A M_{1}$ 和 $A N_{1}$ 的中点 $M_{2}, N_{2}$ ；第三次操作：分别取线段 $A M_{2}$ 和 $A N_{2}$ 的中点 $M_{3}, N_{3}$ ；连续这样操作10次，则每次的两个中点所形成的所有线段之和 $M_{1} N_{1} + M_{2} N_{2} + ⋯ + M_{10} N_{10} =$ （）

A、 $20 - \frac{10}{2^{9}}$ B、 $20 + \frac{10}{2^{9}}$ C、 $20 - \frac{10}{2^{10}}$ D、 $20 + \frac{10}{2^{10}}$

查看试题解析
3. 平面上不重合的两点确定一条直线，不同三点最多可确定3条直线.若平面上不同的n个点最多确定21条直线，则n 的值为.

查看试题解析
4. 如图，直线上有五个点A，B，C，D，E，连结其中两点形成的10个距离，从小到大排列依次为：2，4，5，7，8，k，13，15，17，19，那么k的值是.

查看试题解析
5. 如图，点M在线段AN的延长线上，且线段MN=20，第一次操作：分别取线段AM和AN的中点 $M_{1} ， N_{1}$ ；第二次操作：分别取线段 $A M_{1}$ 和 $A N_{1}$ 的中点 $M_{2}, N_{2}$ ；第三次操作：分别取线段 $A M_{2}$ 和 $A N_{2}$ 的中点 $M_{3}, N_{3}$ ；……连续这样操作10次，则每次的两个中点所形成的所有线段之和 $M_{1} N_{1} + M_{2} N_{2} + \dots + M_{10} N_{10} =$ ( )

A、 $20 - \frac{10}{2^{9}}$ B、 $20 + \frac{10}{2^{9}}$ C、 $20 - \frac{10}{2^{10}}$ D、 $20 + \frac{10}{2^{10}}$

查看试题解析
6.

(1)、在一条直线上有n个点，以这些点为端点的线段共有多少条?

(2)、平面内有n 条两两相交直线，这n条直线最少有几个交点?最多有几个交点?

查看试题解析

二、角中的规律

7. 如图，已知 $∠ A O B = α, ∠ B O C = β, O M$ 平分 $∠ A O C, O N$ 平分 $∠ B O C$ ，则 $∠ M O N$ 的度数是（　　）

A、 $\frac{1}{2} β$ B、 $\frac{1}{2} (α - β)$ C、 $α - \frac{1}{2} β$ D、 $\frac{1}{2} α$

查看试题解析
8. 如图，射线 OB，OC分别在∠AOD，∠BOD的内部，且射线OM，ON分别平分∠AOB，∠COD。若∠MON=a，∠BOC=B，则∠AOD=（）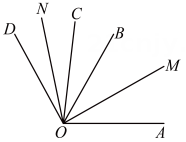

A、2a B、2a-β C、a+β D、a-β

查看试题解析
9. 已知：O是直线AB 上的一点，∠COD 是直角，OE 平分∠BOC.

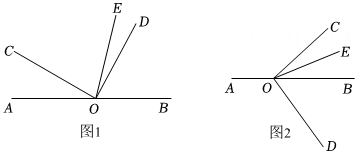(1)、如图①，若∠AOC=30°，求∠DOE 的度数.

(2)、在图①中，若∠AOC=α，直接写出∠DOE 的度数（用含α的代数式表示）.

(3)、将图①中的∠COD 绕顶点O 顺时针旋转至图②的位置.
①探究∠AOC 与∠DOE 的度数之间的关系；
②在 $∠ A O C$ 的内部有一条射线OF，满足∠AOC—4∠AOF= $2 ∠ B O E + ∠ A O F,$ ，试确定∠AOF 与∠DOE 的度数之间的关系，并说明理由.

查看试题解析
10. 如图， $∠ D O E = 50 °$ ．按照下列要求用直尺、量角器继续画图并解决问题：
画出射线 $O A$ ， $O B$ ， $O C$ ，其中 $O E$ 平分 $∠ A O C$ ， $O D$ 平分 $∠ B O C$ ．

(1)、完成图形．

(2)、若 $∠ A O C = 80 °$ ，则∠BOC的大小为______ $°$ ．

(3)、若 $∠ D O E = α$ ， $∠ A O C = 2 β$ （其中 $0 ° < β < α$ ， $0 ° < α + β < 90 °$ ），用含 $α$ ， $β$ 的式子表示出 $∠ B O C$ 的大小为______．

查看试题解析
11. 已知直线 $A B$ 经过点O， $∠ C O D = 90 °$ ， $O E$ 是 $∠ B O C$ 的平分线．

(1)、如图1，若 $∠ A O C = 30 °$ ，求 $∠ D O E$ ；

(2)、如图1，若 $∠ A O C = α$ ，求 $∠ D O E$ ；（用含 $α$ 的式子表示）

(3)、将图1中的 $∠ C O D$ 绕顶点O顺时针旋转到图2的位置，其它条件不变，（2）中的结论___________（填“成立”或“不成立”）；

(4)、将图1中的 $∠ C O D$ 绕顶点O逆时针旋转到图3的位置，其它条件不变，求（2）中的结论是否还成立？试说明理由．

查看试题解析
12. 定义：若 $α - β = 90 °$ ，且 $90 ° < α < 180 °$ ，则我们称 $β$ 是 $α$ 的差余角．例如：若 $α = 110 °$ ，则 $α$ 的差余角 $β = 20 °$ ，

(1)、如图1，点O在直线AB上，射线OE是∠BOC的角平分线，若∠COE是∠AOC的差余角，求∠BOE的度数；

(2)、如图2，点O在直线AB上，若∠BOC是∠AOE的差余角，那么∠BOC与∠BOE有什么数量关系；

(3)、已知，点O在直线AB上，若∠COE是∠AOC的差余角，且OE与OC在直线AB的同侧， $\frac{∠ A O C - ∠ B O C}{∠ C O E}$ 请你探究是否为定值？若是，请求出定值；若不是，请说明理由．

查看试题解析

三、实践探究题

13. 【问题提出】：将长方形的长上随机设置29个点，宽上随机设置19个点（不含长方形的各顶点A、B、C、D，且相对的边点的位置相同），如图连接各边对应的点，则图中一共有             个长方形（包括正方形）？
【问题探究】：为解决上面的问题，我们将采取一般问题特殊化的策略，先从简单和具体的情形入手：
（1）探究一：将一条线段上随机设置n个点，图中一共可以形成多少条线段？
如图1，当 $n = 0$ 时，图中线段有：线段 $A B$ ；共有1条线段；
如图2，当 $n = 1$ 时，以A为端点的线段有：线段 $A C$ 和线段 $A B$ ；以C为端点的有：线段 $C B$ ；共有 $3$ 条线段；
如图3，当 $n = 2$ 时，以A为端点的线段有：线段 $A C$ ， $A D$ ， $A B$ ；以C为端点的有：线段 $C D$ 和线段 $C B$ ；以D为端点的有：线段 $D B$ ；共有 $6$ 条线段；
……，
小结：当随机设置了n个点后，一共可以形成             条线段．（用含n的代数式表示）
（2）探究二：将长方形的长上随机设置m个点，宽上随机设置n个点，则一共有多少个长方形（包括正方形）？
首先我们先探究宽上不设置点的情况．
如图 $4 - 1$ ，当 $m = 0$ ， $n = 0$ 时，
如图 $4 - 2$ ，当 $m = 1$ ， $n = 0$ 时，
如图 $4 - 3$ ，当 $m = 2$ ， $n = 0$ 时，
……，
小结：当长方形的长上随机设置m个点，宽上不设置点，一共有             个长方形．（用含m的代数式表示）
同理，当长方形的长上不设置点，宽上随机设置n个点，一共有             个长方形．（用含n的代数式表示）
如图 $5 - 1$ ，当 $m = 1$ ， $n = 1$ 时，宽上共形成3条线段，图中一共有9个长方形（包括正方形）．
如图 $5 - 2$ ，当 $m = 1$ ， $n = 2$ 时，宽上共形成6条线段，图中一共有18个长方形（包括正方形）．
如图 $5 - 3$ ，当 $m = 2$ ， $n = 1$ 时，宽上共形成3条线段，图中一共有18个长方形（包括正方形）．
如图 $5 - 4$ ，当 $m = 2$ ， $n = 2$ 时，宽上共形成6条线段，图中一共有36个长方形（包括正方形）．
……，
小结：将长方形的长上随机设置m个点，宽上随机设置n个点，连接各边对应的点，则图中一共有             个长方形（包括正方形）．（用含m、n的代数式表示）
【问题解决】：将长方形的长上随机设置29个点，宽上随机设置19个点（不含长方形的各顶点A、B、C、D，且相对的边点的位置相同），如图连接各边对应的点，则图中一共有             个长方形（包括正方形）．（直接写出最后计算结果）






查看试题解析
14. 综合与实践
如图，O为直线 $A B$ 上的一点，过点O作射线 $O C$ ，使 $∠ B O C = 65 °$ ，将一直角三角板的直角顶点放在点O处．

(1)、如图1，将三角板 $M O N$ 的一边 $O N$ 与射线 $O B$ 重合，此时 $∠ M O C =$ ______．

(2)、如图2，将三角板 $M O N$ 绕点O逆时针旋转一定角度，使得 $O C$ 是 $∠ M O B$ 平分线，求 $∠ C O N$ 的度数．

(3)、如图3，将三角板 $M O N$ 持续绕点O逆时针旋转至 $∠ A O C$ 内部，使得 $∠ N O C = \frac{1}{4} ∠ A O M$ ，求 $∠ M O C$ 的度数．

查看试题解析
15. 【问题背景】学习了角的度量单位后，好学的小明在网上搜索发现了如图①所示的量角演示器，他将一副三角尺和量角演示器按如图②所示位置摆放，
【提出问题】

(1)、当活动针 $O E$ 对应的读数为140时， $∠ E O D =$ __________ $°$ ；当活动针 $O E$ 平分 $∠ B O D$ 时， $O E$ 对应的读数为_________ $°$ ．

(2)、将三角尺 $A O B$ 绕着点O以每秒 $4 °$ 的速度按顺时针方向旋转，同时，三角尺 $C O D$ 绕着点O以每秒 $2 °$ 的速度按顺时针方向旋转，当三角尺 $A O B$ 旋转一周时，两把三角尺同时停止转动．
①若在旋转过程中，活动针 $O E$ 始终平分 $∠ B O D$ ．当 $∠ B O D = 60 °$ 时，求旋转所用的时间和活动针 $O E$ 对应的读数；
②若两把三角尺开始旋转时，活动针 $O E$ 同时从 $O B$ 的位置绕着点O以每秒 $7 °$ 的速度按顺时针方向旋转，当 $O E$ 与 $O D$ 重合后，活动针 $O E$ 立即以同样的速度逆时针方向旋转．当 $O E$ 与 $O B$ 重合后停止旋转，求活动针 $O E$ 停止时对应的读数，请直接写出答案（结果保留整数）．

查看试题解析
16.

(1)、特例感知：如图 $1$ ，线段 $M N = 20 c m$ ， $A B = 2 c m$ ，线段 $A B$ 在线段 $M N$ 上运动（点 $A$ 不超过点 $M$ ，点 $B$ 不超过点 $N$ ）， $C 、 D$ 分别是 $A M 、 B N$ 的中点．在线段 $A B$ 运动的过程中，线段 $C D$ 的长度是否发生变化？如果不变，求出 $C D$ 的长度；如果变化，请说明理由；

(2)、知识迁移：我们发现角的很多规律和线段一样，如图 $2$ ， $∠ A O B$ 在 $∠ M O N$ 内部转动，射线 $O C$ 和射线 $O D$ 分别平分 $∠ A O M$ 和 $∠ B O N$ ． ①若 $∠ M O N = 150 °$ ， $∠ A O B = 30 °$ ，则 $∠ C O D =$ ▲ $°$ ；
②请你猜想 $∠ A O B$ ， $∠ C O D$ 和 $∠ M O N$ 三个角具有怎样的数量关系，并说明理由；

(3)、类比探究：如图 $3$ ， $∠ A O B$ 在 $∠ M O N$ 内部转动，若 $∠ M O N = 155 °$ ， $∠ A O B = 25 °$ ， $∠ M O C = m ∠ A O C$ ， $∠ N O D = m ∠ B O D$ ，直接写出用含有 $m$ 的式子表示 $∠ C O D$ 的度数．

查看试题解析
17. 十八世纪瑞士数学家欧拉证明了简单多面体的顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式.请你观察图中几种简单多面体模型，解答下列问题：

(1)、根据图中的多面体模型，填写表格中的空格：
多面体
顶点数（V）
面数（F）
棱数（E）
四面体
4
4
6
正方体
8
6

八面体
8
12
十二面体
20
12
30

(2)、根据上面的表格，猜想顶点数（V）、面数（F）、棱数（E）之间存在的关系式是（用所给的字母表示）.

(3)、若一个多面体的面数比顶点数少14，且有48条棱，则这个多面体的面数是.

(4)、有一个玻璃饰品的外形是简单多面体，它共有24个顶点，每个顶点处都有 3条棱，设该多面体的面数为x，求x的值.

查看试题解析

多面体	顶点数（V）	面数（F）	棱数（E）
四面体	4	4	6
正方体	8	6
八面体		8	12
十二面体	20	12	30