人教版九(上)第二十三章 旋转 单元测试卷
试卷更新日期:2025-09-25 类型:单元试卷
一、选择题
-
1. 教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育,下列安全图标既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,中, , 将绕点顺时针旋转 , 得到 , 边与边交于点(不在上),则的度数为( )
2. 如图,中, , 将绕点顺时针旋转 , 得到 , 边与边交于点(不在上),则的度数为( ) A、 B、 C、 D、3. 如图,可由旋转而成,点的对应点是 , 点的对应点是 , 在平面直角坐标系中,三点坐标为 , , , 则旋转中心的坐标为( )
A、 B、 C、 D、3. 如图,可由旋转而成,点的对应点是 , 点的对应点是 , 在平面直角坐标系中,三点坐标为 , , , 则旋转中心的坐标为( ) A、 B、 C、 D、4. 已知点和点关于原点对称,则 ( )A、1 B、 C、3 D、5. 如图,中, , 将绕点B逆时针旋转得 , 若点在上,则的长为( )
A、 B、 C、 D、4. 已知点和点关于原点对称,则 ( )A、1 B、 C、3 D、5. 如图,中, , 将绕点B逆时针旋转得 , 若点在上,则的长为( ) A、 B、4 C、 D、56. 如图,已知正方形的边长为3,E、F分别是边上的点,且 , 将绕点D逆时针旋转 , 得到 . 若 , 则的长为( ).
A、 B、4 C、 D、56. 如图,已知正方形的边长为3,E、F分别是边上的点,且 , 将绕点D逆时针旋转 , 得到 . 若 , 则的长为( ).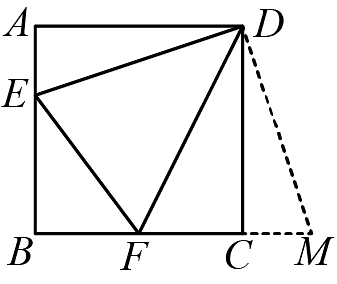 A、 B、2 C、 D、7. 如图,在中, , , 把绕着点逆时针旋转得到 , 其中点落在边的上,则的度数为( )
A、 B、2 C、 D、7. 如图,在中, , , 把绕着点逆时针旋转得到 , 其中点落在边的上,则的度数为( ) A、 B、 C、 D、8. 如图,点A的坐标是 , 将线段绕点O顺时针旋转 , 点A的对应点的坐标是( )
A、 B、 C、 D、8. 如图,点A的坐标是 , 将线段绕点O顺时针旋转 , 点A的对应点的坐标是( ) A、 B、 C、 D、9. 如图,将边长为2的正方形绕点按逆时针旋转到正方形的位置,且点落在对角线上,与相交于点 , 则的长为( )
A、 B、 C、 D、9. 如图,将边长为2的正方形绕点按逆时针旋转到正方形的位置,且点落在对角线上,与相交于点 , 则的长为( ) A、1 B、 C、 D、10. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( )
A、1 B、 C、 D、10. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( ) A、6 B、3 C、2 D、1.5
A、6 B、3 C、2 D、1.5二、填空题
-
11. 若点与点关于原点对称,则 .12. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点逆时针旋转50°到△的位置,则∠=度.
 13. 与抛物线关于原点成中心对称的抛物线的函数解析式为 .14. 如图所示,在正方形ABCD中,AC,BD相交于点O,AOE绕点O逆时针旋转90°后与BOF重合,AB=2,则四边形BEOF面积是 .
13. 与抛物线关于原点成中心对称的抛物线的函数解析式为 .14. 如图所示,在正方形ABCD中,AC,BD相交于点O,AOE绕点O逆时针旋转90°后与BOF重合,AB=2,则四边形BEOF面积是 .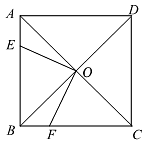 15. 如图,在长方形ABCD中, , 点P为边AD上的一个动点,以BP为边向右作等边 , 连接 . 当点落在边BC上时,的度数为;当线段的长度最小时,的度数为 .
15. 如图,在长方形ABCD中, , 点P为边AD上的一个动点,以BP为边向右作等边 , 连接 . 当点落在边BC上时,的度数为;当线段的长度最小时,的度数为 .
三、解答题
-
16. 如图所示,在中, , 将绕点A逆时针旋转至处,使点B落在BC延长线上的D点处,求的度数.
 17. 如图将绕点A逆时针旋转得到 , 点C和点E是对应点,若 , , 求BD的长.
17. 如图将绕点A逆时针旋转得到 , 点C和点E是对应点,若 , , 求BD的长.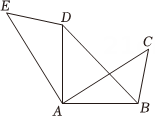 18. 如图,在中, , . 将绕点B按逆时针方向旋转得 , 使点C落在AB边上,点A的对应点为点D,连接AD,求的度数.
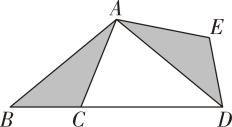
18. 如图,在中, , . 将绕点B按逆时针方向旋转得 , 使点C落在AB边上,点A的对应点为点D,连接AD,求的度数. 19. 如图,是经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
19. 如图,是经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题: (1)、请按顺序写出点A,E,C的对应点的坐标,并说说对应点的坐标有哪些特征;
(1)、请按顺序写出点A,E,C的对应点的坐标,并说说对应点的坐标有哪些特征;与D ;B 与;与F ;对应点坐标的特征是横坐标、纵坐标均 ;
(2)、若点与点也是通过上述变换得到的对应点,求a,b的值.20. 将一副直角三角板如图1,摆放在直线MN上(直角三角板和直角三角板 , , , , ),保持三角板不动,将三角板绕点以每秒的速度顺时针旋转,旋转时间为秒,当与射线重合时停止旋转. (1)、如图2,当为的角平分线时,求此时t的值;(2)、当旋转至的内部时,求与的数量关系;(3)、在旋转过程中,当三角板的其中一边平行于三角板的某一边时,求此时t等于 (直接写出答案即可).21. 在矩形中,点E在边上, , 将绕点B顺时针旋转得到 , 使点A的对应点F在线段上.
(1)、如图2,当为的角平分线时,求此时t的值;(2)、当旋转至的内部时,求与的数量关系;(3)、在旋转过程中,当三角板的其中一边平行于三角板的某一边时,求此时t等于 (直接写出答案即可).21. 在矩形中,点E在边上, , 将绕点B顺时针旋转得到 , 使点A的对应点F在线段上. (1)、请在图中作出;(要求:尺规作图,不写作法,保留作图痕迹)(2)、与交于点Q,连接 , 若 , 请探究与的数量关系.22. 小明在一次数学活动中,进行了如下的探究活动:如图,在矩形中, , , 以点为中心,顺时针旋转矩形 , 得到矩形 , 点、、的对应点分别为、、 .
(1)、请在图中作出;(要求:尺规作图,不写作法,保留作图痕迹)(2)、与交于点Q,连接 , 若 , 请探究与的数量关系.22. 小明在一次数学活动中,进行了如下的探究活动:如图,在矩形中, , , 以点为中心,顺时针旋转矩形 , 得到矩形 , 点、、的对应点分别为、、 . (1)、如图①,当点落在边上时,求的长;(2)、如图②,当点落在线段上时,与交于点 . 求的长.(3)、记点为矩形对角线的交点,连接、 , 记面积为 , 求的取值范围.23. 已知在平面直角坐标系中,点 .
(1)、如图①,当点落在边上时,求的长;(2)、如图②,当点落在线段上时,与交于点 . 求的长.(3)、记点为矩形对角线的交点,连接、 , 记面积为 , 求的取值范围.23. 已知在平面直角坐标系中,点 . (1)、如图,点C在线段上(不与A、B重合)移动, , 且 , 猜想线段之间的数量关系并证明你的结论;(2)、若P为x轴正半轴上异于原点O的一个动点,连接 , 将线段绕点P顺时针旋转至 , 直线交y轴于点Q,
(1)、如图,点C在线段上(不与A、B重合)移动, , 且 , 猜想线段之间的数量关系并证明你的结论;(2)、若P为x轴正半轴上异于原点O的一个动点,连接 , 将线段绕点P顺时针旋转至 , 直线交y轴于点Q,①当P点在x轴上移动时,试判断线段的长是否会发生变化,如果不变求出线段的长,如果发生变化请说明理由;
②连接 , 直接写出线段的最小值.