人教版数学七年级上学期重难点复习3：一元一次方程及应用

试卷更新日期：2025-09-25 类型：复习试卷

进入出卷网下载

一、一元一次方程的相关概念

1. 下列四个方程中，一元一次方程是（）

A、 $x + y = 1$ B、 $x + \frac{1}{x} = 1$ C、 $x^{2} - x + 2 = 0$ D、 $x + 1 = 2 x + 1$

查看试题解析
2. 关于x的方程 $x^{k - 1} + 1 = 5$ 是一元一次方程，则k的值为（）．

A、 $k = 1$ B、 $k = 2$ C、 $k = 3$ D、 $k = 0$

查看试题解析
3. 方程3x-5=4x+8经移项得3x-4x=8+5，这实际上是在方程两边都加上（）

A、4x-5 B、4x+5 C、-4x-5 D、-4x+5

查看试题解析
4. 已知 $x = 1$ 是关于 $x$ 的方程 $a x - 2 x + 5 = 0$ 的解，则 $a$ 的值是（）

A、-5 B、-6 C、-3 D、8

查看试题解析
5. 下列方程变形中，错误的是（）

A、 $2 x + 6 = 0$ 变形为 $2 x = - 6$ B、 $- \frac{x + 1}{2} = \frac{1}{2}$ 变形为 $- x + 1 = 1$ C、 $- 2 (x - 4) = 2$ 变形为 $x - 4 = - 1$ D、 $\frac{x + 3}{2} = x + 2$ 变形为 $x + 3 = 4 + 2 x$

查看试题解析
6. 将方程 $\frac{x}{3} - 1 = \frac{3 - 2 x}{4}$ 去分母得（）

A、 $4 x - 1 = 3 (3 - 2 x)$ B、 $4 x - 12 = 3 (3 - 2 x)$ C、 $4 x - 1 = 3 - 2 x$ D、 $4 x - 12 = 3 - 2 x$

查看试题解析
7. 阅读框图，在四个步骤中，依据“等式性质”的步骤是（填序号）．
解： $4 - 7 x = 2 (3 - x)$
去括号得： $4 - 7 x = 6 - 2 x$ …………①
移项得： $- 7 x + 2 x = 6 - 4$ …………②
合并同类项得： $- 5 x = 2$ …………③
系数化为1得： $x = - \frac{2}{5}$ …………④

查看试题解析

二、解一元一次方程

8. 在解方程 $\frac{2 x - 1}{3} = 1 - \frac{x - 2}{6}$ 时，小江的解法如下：
解：去分母，得2（2x-1）=6-x-2...第①步
去括号，得4x-2=6-x-2..第②步
移项，得4x+x=6-2+2...第③步
则5x=6..第④步
解得x= $\frac{6}{5}$ ..第⑤步
小江同学的解法正确吗?若不正确，请指出他在第 ▲ 步开始出现错误，并写出
正确的解题过程.

查看试题解析
9. 解方程：

(1)、1-3（x-3）=2x

(2)、 $\frac{3 x - 2}{3} = \frac{4 x - 1}{6} - 1$

查看试题解析
10. 解方程

(1)、 $\frac{x - 5}{3} - \frac{1}{4} x = - 1$ ；

(2)、 $x - 2 (x + \frac{1}{2}) = 3 (x - 4)$ ．

查看试题解析
11. 解方程

(1)、 $8 (2 x - 4) = 4 - 6 (4 - x)$

(2)、 $x - \frac{x - 1}{2} = 2 +$ $\frac{x + 2}{3}$ ．

查看试题解析

三、含参的一元一次方程

12. 已知关于 $x$ 的一元一次方程 $\frac{1}{2025} x + 3 = 4 x - m$ 的解为 $x = 2024$ ，则关于 $y$ 的一元一次方程 $\frac{1}{2025} (y + 1) - 3 = 4 (y + 1) + m$ 的解为 $y =$ ．

查看试题解析
13. 方程 $2 - 3 (x + 1) = 0$ 的解与关于x的方程 $\frac{k + x}{2} - 3 k - 2 = 2 x$ 的解互为倒数，求k的值.

查看试题解析
14. 嘉琪在做课本上的随堂练习解方程： $2 - (■ - x) = - 2$ 时，不小心将墨迹盖住了一个数字，跟同桌咨询后得知该方程的解为 $x = - 3$ ，求“■”处被墨盖住的数应该是多少？

查看试题解析
15. 若关于x的方程2x﹣3=1和 $\frac{x - k}{2} = k - 3 x$ 有相同的解，求k的值．

查看试题解析
16. 小马虎解关于x的方程 $\frac{2 x - 1}{3} = \frac{x + a}{2} - 1 ，$ 去分母时，两边同时乘6，然而方程右边的“-1”忘记乘6，因而求得的解为x $= 4$ .求：

(1)、 $a^{2024}$ 的值.

(2)、此方程正确的解.

查看试题解析
17. 已知a，b为常数，关于x的方程 $\frac{k x + a}{3} = 1 - \frac{2 x + b k}{6},$ 无论k为何值，它的解总是x=2，求a+b的值.

查看试题解析
18.

(1)、圆圆同学发现关于x的代数式（2k-1）x+k+3一个有意思的性质：当x取某一特殊值x₀时，无论 k 的值如何变化，这个代数式的值都是定值.请你求出x₀及该定值.

(2)、已知关于x 的二次三项式 $a x^{2} - (a - b) x - b + 3,$ 当x取某一特殊值x₀时，无论a，b如何变化，代数式的值都是定值，请求出x₀及该定值.

查看试题解析

四、一元一次方程的应用

19. 某景区定制一批文创用品，要求每套文创用品中包括2个书签和1个冰箱贴。已知生产厂家共有70位工人，每位工人每天可生产15个书签，或生产10个冰箱贴。问厂家如何安排工人才能使得每天生产的书签和冰箱贴刚好配套？若设安排x位工人生产书签，则根据题意可列方程（）

A、10x=2×15 （70- x） B、15x=2×10 （70-x） C、2×10x=15 （70-x） D、2×15x=10 （70-x）

查看试题解析
20. 《九章算术》是中国传统数学最重要的著作之一，书中记载：“今有人共买鸡，人出九，盈十一：人出六，不足十六，问人数几何？”意思是：“有若干人共同出钱买鸡，如果每人出九钱，那么多了十一钱：如果每人出六钱，那么少了十六钱．问：共有几个人？”设有x个人共同买鸡，依题意可列方程为（）

A、 $9 x - 11 = 6 x + 16$ B、 $9 x + 11 = 6 x - 16$ C、 $\frac{x - 11}{9} = \frac{x + 16}{6}$ D、 $\frac{x + 11}{9} = \frac{x - 16}{6}$

查看试题解析
21. 由于换季，商场准备对某商品打折出售，如果按原售价的七折出售，将亏损40元，而按原售价的八五折出售，将盈利20元，则该商品的进货价为元．

查看试题解析
22. 2024 年，盲盒风潮依旧不减，各款盲盒层出不穷，让人眼花缭乱．镇海区某工厂共有 800名工人，负责生产 $A, B$ 两种盲盒。

(1)、若该工厂生产盲盒 $A$ 的人数比生产盲盒 $B$ 的人数的 3 倍少 200 人，请求出生产盲盒 $B$ 的工人人数；

(2)、为了促销，工厂按商家要求生产盲盒大礼包，该大礼包由 3 个盲盒 $A$ 和 4 个盲盒 $B$ 组成．已知每个工人平均每天可以生产 10 个盲盒 $A$ 或 20 个盲盒 $B$ ，且每天只能生产其中的一种盲盒．该工厂应该安排多少名工人生产盲盒 $A$ ，多少名工人生产盲盒 $B$ 才能使每天生产的盲盒正好配套？

查看试题解析
23. 工业园区某机械厂的一个车间主要负责生产螺丝和螺母，该车间有工人44人，其中女生人数比男生人数的2倍少10人，每个工人平均每天可以生产螺丝50个或者螺母120个．

(1)、该车间有男生、女生各多少人？

(2)、已知一个螺丝与两个螺母配套，为了使每天生产的螺丝螺母恰好配套，应该分配多少工人负责生产螺丝，多少工人负责生产螺母？

查看试题解析
24. 美丽嵊州吸引了很多游客，使民宿经济得到蓬勃发展，甲、乙两个旅行团同时来嵊州旅游，住进了西白山下的同一家农家乐．已知乙团人数比甲团人数多4人，两团人数之和等于72人．
（1）问甲、乙两个旅行团的人数各是多少人？
（2）若乙团中儿童人数恰为甲团中儿童人数的3倍少2人，农家乐消费标准为每人每天90元，儿童6折优惠，其余不优惠，若两旅行团在此农家乐每天消费的费用相同，求甲、乙两团儿童人数各是多少人．

查看试题解析

五、实践探究题

25. 根据表中的素材，完成下面的任务：

如何设计奖品购买及兑换方案？
素材 1	文具店销售某种钢笔与笔记本，已知钢笔每支 10 元，笔记本每本 5 元.
素材 2	学校用 1100 元购买这种钢笔和笔记本，其数量之比为 $4 : 3$ .
素材 3	文具店开展 "满送" 优惠活动，每满 130 元送1 张兑换券，满 260 元送 2 张兑换券，以此类推. 学校花费 1100 元后，将兑换券全部用于商品兑换最终，笔记本与钢笔数量相同.

(1)、【任务一：探究购买方案】分别求出换前购买钢笔和笔记本的数量.

(2)、【任务二：确定兑换方式】求出用于兑换钢笔的兑换券的张数.

查看试题解析

26. 七年级数学兴趣小组成员自主开展数学微项目研究，他们决定研究宁波地铁的运行．

素材 1

宁波轨道交通 1 号线是宁波第 1 条建成运营的地铁线路，极大地便利了市民的日常出行．为了研究方便，地铁运行过程中速度看成恒定，每相邻两站的间距都可近似看成相等，且每相邻两站之间地铁的运行时间都为 2 分钟，每站停靠时间 30 秒．如图 1 是 1 号线部分线路图：

素材 2

小明觉得可以用数轴上的动点来刻画地铁的运行过程，他以东门口站为原点，建立了如下图 2的数轴．其中数字 1 代表江厦桥东站，数字 2 代表舟孟北路站，以此类推．数轴上的动点 $P$ 可以用来刻画运动的地铁，动点 $P$ 每次运动到一个整数点时，都需要暂停 30 秒，代表地铁到站停靠．

(1)、图2 中数字 5 代表站．

(2)、如图 2，动点

P

从原点出发，运动

t

分钟到数字 3 和数字 4 之间时（不含数字 3 和数字 4），求点

P

在数轴上表示的数（用含

t

的代数式表示）．

(3)、如图 3，

A

从江厦桥东站上车，往东环南路方向乘坐地铁，同时

B

从福庆北路站上车，往东门口方向坐地铁．若两辆地铁恰好同时从江厦桥东和福庆北路出发，则出发多久后两人在数轴上刚好相距 2.5 个单位长度．

查看试题解析

27. 根据一下素材，探索完成任务：

如何设计宣传牌?
素材1	一块长方形宣传牌如图(a)所示，长330cm，宽220cm，拟在上面书写24个字，宣传牌中间可以用来设计的部分也是长方形，且长是宽的1.55倍；四周空白部分的宽度相等.
素材2	如图(b)所示，为了美观，将设计部分分成大小相等的上、中、下三个长方形栏目，栏日与栏日之间的中缝间距相等.
素材3	如图(c)所示，每栏划出正方形方格，中间有十字间隔，横向两行中间间隔和竖向中间间隔宽度比为1：2.

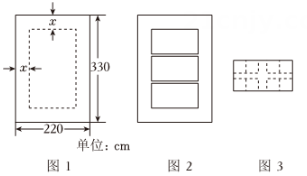
任务1	(1)分析数量关系.设四周宽度为xcm，用含x的代数式分别表示设计部分的长和宽
任务2	(2)确定四周宽度，求出四周宽度x的值.
任务3	(3)确定栏目大小. ①求每个栏目的竖直高度； ②求长方形栏目与栏目之间中缝的间距

查看试题解析

28. 【综合与实践】

木杆与重物

学习了一元一次方程后，老师在综合实践课上让同学们探讨木杆与重物的实验问题，实验通过改变L₂的长度和砝码的重量来保持木杆的平衡，并用表格记录了实验数据如下：

【实践发现】

实验次数	左边		右边
实验次数	砝码重量M₁（克）	支点O到左边挂重物处的距离L₁（cm）	砝码重量M₂（克）	支点O到右边挂重物处的距离L₂（cm）
1	20	40	20	40
2	20	40	40	20
3	20	40	60	13.33
4	20	40	80	10
5	20	40	100	8
…	M₁	L₁	M₂	L₂

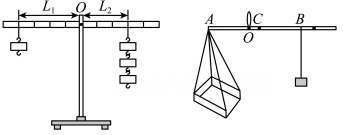
小明从表中发现这样的规律： $20 \times 40 = 20 \times 40$ ，

$20 \times 40 = 40 \times 20$ ，

$20 \times 40 = 60 \times 13.33$ ，

$20 \times 40 = 80 \times 10$ ，

$20 \times 40 = 100 \times 8$ ， …

$M_{1} \times L_{1} = M_{2} \times L_{2}$ .

【实践运用】根据上面规律解决下列问题：

(1)、若

20 \times 40 = 50 \times L_{2}

，则L₂=cm；

(2)、若M₁的重量是50克，L₁的长度是40cm，L₂的长度是10cm，则M₂等于多少克才能保持木杆平衡？

(3)、学习小组根据这个原理自制了一个杆秤，如图所示，提纽处O是支点，已知AO为5cm，秤砣重量是500克，不放重物时，秤砣放在C处时秤杆平衡，此时

C O = 1 c m

，放入重物时，秤砣放在B处时秤杆平衡，此时

B O = 21 c m

，则重物的重量约是多少斤？（1斤=500克）

查看试题解析

29. 某学习小组开展了以“居民用电如何计费”为主题的项目化学习．

学习小组首先了解了浙江省电网销售电价：

单位：元/千瓦时（含税）

	普通电价	峰时电价	谷时电价
第一阶梯：年用电量2760千瓦时及以下部分	0.5380	0.5680	0.2880
第二阶梯：年用电量2760~4800（不包含2760）千瓦时部分	0.5880	0.6180	0.3380
第三阶梯：年用电量4800（不包含4800）千瓦时以上部分	0.8380	0.8680	0.5880

备注：居民生活用电分时电价时段划分：高峰时段：8：00-22：00，低谷时段：22：00-次日8：00．

然后对“月用电量200千瓦时（其中峰电100千瓦时）需缴多少电费？”探究结果如下：

	不使用峰谷电	使用峰谷电
第一阶梯	$200 \times 0.5380 = 107.6$ （元）	$100 \times 0.5680 + 100 \times 0.2880 = 85.6$ （元）
第二阶梯	$200 \times 0.5880 = 117.6$ （元）	②________元
第三阶梯	①________元	$100 \times 0.8680 + 100 \times 0.5880 = 145.6$ （元）

请依据上述素材，解答下列问题：

(1)、填空：表中①________；②________

(2)、已知晶晶家在2024年5月用电量为300千瓦时，且处于第一阶梯，她建议爸爸妈妈申请办理峰谷电，因为用峰谷电可以使本月电费减少

41.4

元，请问晶晶家5月份用了多少千瓦时的峰电，多少千瓦时的谷电？

(3)、2024年10月份小菲家用电量为200千瓦时，小华家用电量比小菲家少，在两家都不使用峰谷电的情况下，小华家的当月电费却超过了小菲家

18.1

元，求小华家当月用电量（结果精确到1千瓦时）．

查看试题解析

30. 综合与实践：设计完成工程的最短工期方案（最短工期是指完成某项工程所需的最短时间）．
【背景素材】某公司要生产某大型产品60件，已知甲，乙，丙三家子工厂完成一件产品的时间分别为4天，6天，5天．现计划：①三家子工厂同时开始生产；②分配给甲工厂的数量是丙的2倍．
【问题解决】为设计方案，可以通过特殊情况或满足部分条件逐步进行探究．

(1)、思考1（特值分析）：若该公司将20件产品分配给甲工厂，则最短工期为多少天？

(2)、思考2（减少要素）：若不考虑素材②，仅由甲、乙两工厂完成，则当两家工厂同时完成生产时工期最短，求如何分配产品件数与最短工期．

(3)、思考3（方案探究）：如何分配三家工厂的生产任务使得工期最短，并求出最短工期．（注：如你直接挑战思考3并正确解答也给满分）

查看试题解析
31. 综合与实践：在学习《整式的加减》时，我们探究了月历中数字之间的关系和变化规律．已知月历中同行的数从左向右依次递增1，同列的数从上向下依次递增7．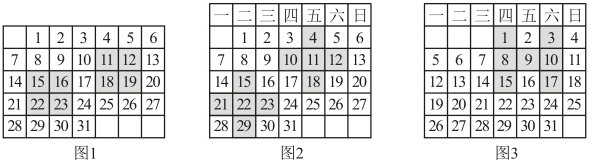

(1)、探究1  图1是某月的月历，现要探究带阴影的“口”字方框中的4个数（框中圈出的数没有空白）的数量关系，方框可以任意移动；小明是先假设左上角的数为m ，他通过计算发现斜对角的两个数字之和均为，从而他得出结论：“口”字方框中的4个数满足斜对角两数之和（填“相等”或“不相等”）；

(2)、探究2  小明又探究了图2中带阴影的十字方框中的5个数（框中圈出的数没有空白）的数量关系，发现当十字框任意移动位置时这5个数之和总是5的倍数，请你通过计算说明他的结论成立的理由；

(3)、探究3  小明还探究了在图3中任意选取“H”形框中的7个数（如阴影部分所示）的规律，他认为这7个数的和可以是133，你认为他的说法正确吗？并说明理由．

查看试题解析