期中素养综合测试卷 提升卷——湘教版(2024)数学八(上)期中分层测(范围:1-3章)
试卷更新日期:2025-09-24 类型:期中考试
一、选择题
-
1. 的倒数是( )A、 B、 C、 D、2. 要使有意义,则x的取值范围是( )A、 B、 C、且 D、且3. 下列多项式中,不能用完全平方公式分解因式的是( )A、 B、 C、 D、4. 已知 , , 则代数式的值为( )A、9 B、 C、3 D、55. 对于分式( , 为常数),若当时,该分式总有意义;当时,该分式的值为负数.则 , 与的大小关系正确的是( )A、 B、 C、 D、6. 把多项式 因式分解之后,正确的结果是( ).A、(x+y+3)(x-y-1) B、(x+y-1)(x-y+3) C、(x+y-3)(x-y+1) D、(x+y+1)(x-y-3)7. 已知 , , 则的值为( )A、 B、 C、 D、8. 若运算的结果为整式,则“□”中的式子可能是( )A、 B、 C、 D、9. 已知实数满足 , 则代数式的值为( )A、9 B、7 C、0 D、10. 化简的结果是( )A、 B、 C、 D、
二、填空题
-
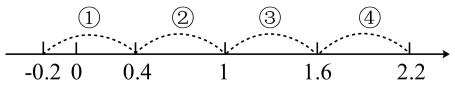
11. 化简 =.12. 若分式 的值为 ,则 的值为.13. 已知 , 则代数式的值为 .14. 若多项式分解因式的结果为 , 则的值为 .15. 若 , 则的值是 .16. 如图,数轴上有四条线段分别标有①,②,③,④,则表示分式 的值的点应落在数轴的段.(填序号)
 17. 若关于的不等式组无解,且关于的分式方程有正整数解,则满足条件的所有整数的和为 .18. 如果无理数m的值介于两个连续正整数之间,即满足(其中a、b为连续正整数),我们则称无理数m的“神奇区间”为 . 例: , 所以的“神奇区间”为 . 若某一无理数的“神奇区间”为 , 且满足 , 其中 , 是关于x、y的二元一次方程组的一组正整数解,则 .
17. 若关于的不等式组无解,且关于的分式方程有正整数解,则满足条件的所有整数的和为 .18. 如果无理数m的值介于两个连续正整数之间,即满足(其中a、b为连续正整数),我们则称无理数m的“神奇区间”为 . 例: , 所以的“神奇区间”为 . 若某一无理数的“神奇区间”为 , 且满足 , 其中 , 是关于x、y的二元一次方程组的一组正整数解,则 .三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、;(2)、21. 已知m为整数,试说明 一定能被8整除.22. 义务献血利国利民,是每个健康公民应尽的义务。一个采血点通常在规定时间接受献血,采血结束后,再统一送到市中心血库,且采血和送到血库的时间必须在4小时内完成,超过4小时送达,血液将变质. 已知A、 B两个采血点到中心血库的路程分别为30km、36km,经过了解获得A、B两个采血点的运送车辆有如下信息:
信息一: B采血点运送车辆的平均速度是A采血点运送车辆的平均速度1.2倍;
信息二:A、B两个采血点运送车辆行驶的时间之和为2小时.
(1)、 求A、B两个采血点运送车辆的平均速度各是多少?(2)、若B采血点完成采血的时间为2.5小时,判断血液运送到中心血库后会不会变质?23. 常用的因式分解的方法有:提公因式法和公式法,但有的多项式用上述方法无法分解,例如 , 我们细心观察就会发现,前两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整的分解了,具体分解过程如下:这种方法叫分组分解法,请利用这种方法因式分解下列多项式:
(1)、;(2)、;(3)、 .24. 求代数式的值,其中 . 下面是小芳和小亮的解题过程,都是把含有字母式子先开方再进行运算的方法,请认真思考、理解解答过程,回答下列问题.小芳:
解:原式 ,
小亮:
解:原式= .
(1)、______的解法是错误的;(2)、求代数式的值,其中 .