人教版数学七年级上学期重难点复习2:整式的加减
试卷更新日期:2025-09-24 类型:复习试卷
一、代数式及代数式的值
-
1. 当时,代数式的值是8,则当时,这个代数式的值是( )A、 B、4 C、8 D、62. 如图,乐乐将 , , , 0,1,2,3,4,5分别填入九个空格内,使每一行、每一列、每条对角线上的三个数之和相等,若a,b,c分别表示其中的一个数,则的值为( )
 A、0 B、-1 C、-2 D、-33. 若 , 则的值为 .4. 若a2﹣3b=6,则4(a2﹣3b)2﹣2a2+6b+4= .5. 如图,现有五张图 1 所示形状大小完全相同的小长方形,长为 ,宽为 ,将它们放入图 2 的大长方形 中,若未被覆盖的两个阴影部分的周长分别记为 和 与 的差等于两倍的小长方形的宽,则小长方形的长与宽满足( )
A、0 B、-1 C、-2 D、-33. 若 , 则的值为 .4. 若a2﹣3b=6,则4(a2﹣3b)2﹣2a2+6b+4= .5. 如图,现有五张图 1 所示形状大小完全相同的小长方形,长为 ,宽为 ,将它们放入图 2 的大长方形 中,若未被覆盖的两个阴影部分的周长分别记为 和 与 的差等于两倍的小长方形的宽,则小长方形的长与宽满足( )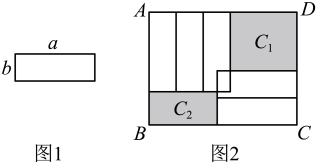 A、 B、 C、 D、6. 我们知道, , 类似地,我们也可以将看成一个整体,则 . 整体思想是数学解题中一种重要的思想方法,它在多项式的化简和求值中有着广泛的应用.请根据上面的提示和范例,解决下面的问题:(1)、把看成一个整体,则将合并的结果为_____(2)、已知 , 求的值.(3)、已知 , , , 求的值.
A、 B、 C、 D、6. 我们知道, , 类似地,我们也可以将看成一个整体,则 . 整体思想是数学解题中一种重要的思想方法,它在多项式的化简和求值中有着广泛的应用.请根据上面的提示和范例,解决下面的问题:(1)、把看成一个整体,则将合并的结果为_____(2)、已知 , 求的值.(3)、已知 , , , 求的值.二、整式的加减
-
7. 以下是嘉淇做填空题的结果:
 , 已知她的计算结果是正确的,但“
, 已知她的计算结果是正确的,但“ ”处被墨水弄脏看不清了,“
”处被墨水弄脏看不清了,“ ”处应是( ) A、 B、 C、 D、8. 已知 , .(1)、求 .(2)、如果 , 求的表达式.9. 已知 .(1)、当时,求的值;(2)、若的值与的取值无关,求的值.10. 若(1)、化简:7M-2[M-(N-3M)];(2)、当 时,求(1)中代数式的值.11. 已知整式.(1)、若的值与的取值无关,则;(2)、当 , 时.
”处应是( ) A、 B、 C、 D、8. 已知 , .(1)、求 .(2)、如果 , 求的表达式.9. 已知 .(1)、当时,求的值;(2)、若的值与的取值无关,求的值.10. 若(1)、化简:7M-2[M-(N-3M)];(2)、当 时,求(1)中代数式的值.11. 已知整式.(1)、若的值与的取值无关,则;(2)、当 , 时.①化简;
②当整式取得最小值时,此时的值为.
三、整式加减图形应用
-
12. 用4个完全相同的边长为的小长方形(如图1)和两个阴影部分的长方形拼成1个宽()为6的大长方形(如图2).
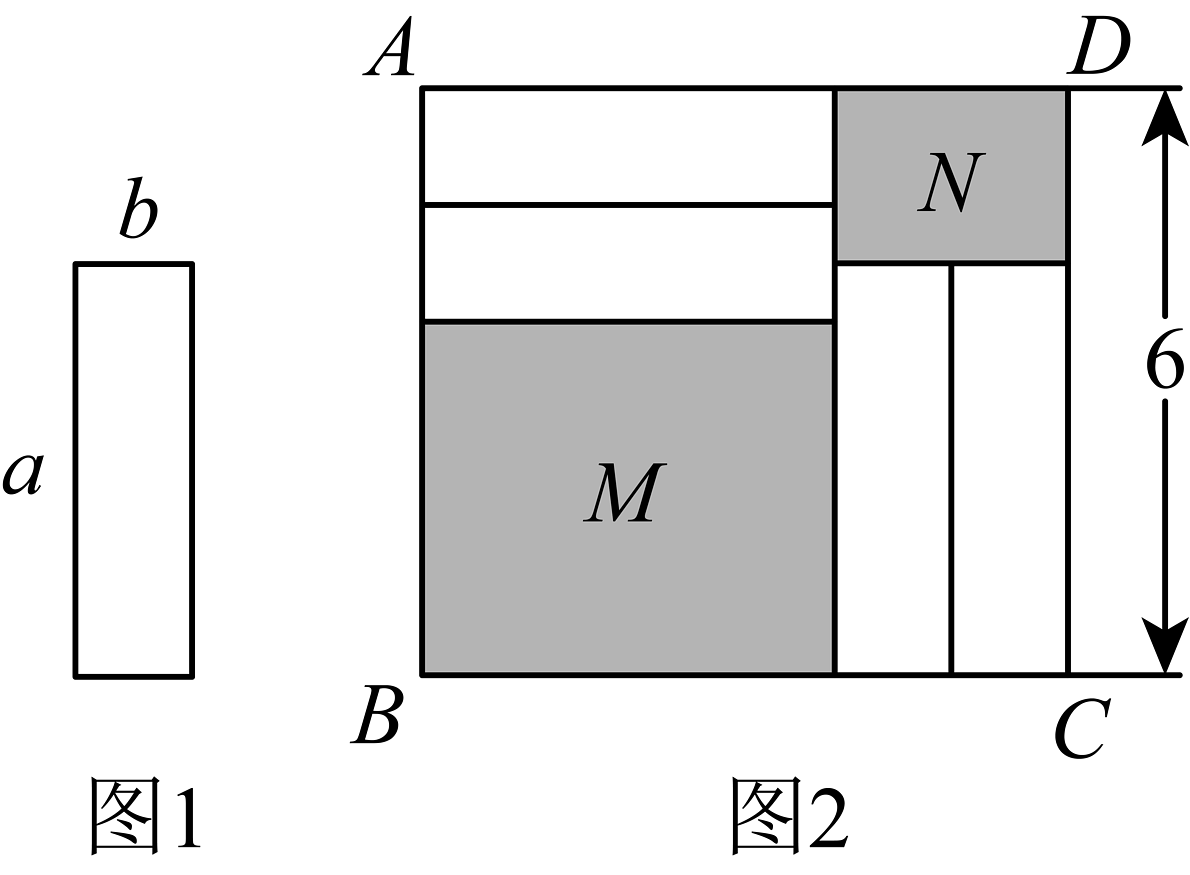 (1)、请用含的代数式表示:①的长;②阴影的面积;(2)、说明阴影与阴影的周长的和与的关系.13. 如图,正方形和正方形的边长分别为a和4.
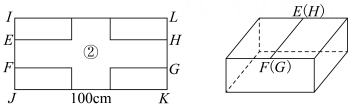
(1)、请用含的代数式表示:①的长;②阴影的面积;(2)、说明阴影与阴影的周长的和与的关系.13. 如图,正方形和正方形的边长分别为a和4. (1)、写出表示阴影部分面积的代数式(结果要求化简);(2)、求时阴影部分的面积.14. 如图,已知长方形 , 将三个完全相同的长为、宽的长方形放入其中,其中他们的重叠部分是两个相同的正方形,则阴影部分①周长与阴影部分②的周长之和为( )
(1)、写出表示阴影部分面积的代数式(结果要求化简);(2)、求时阴影部分的面积.14. 如图,已知长方形 , 将三个完全相同的长为、宽的长方形放入其中,其中他们的重叠部分是两个相同的正方形,则阴影部分①周长与阴影部分②的周长之和为( ) A、 B、 C、 D、40015. 如图,红军西征胜利纪念馆要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,尺寸如图所示(单位:米).
A、 B、 C、 D、40015. 如图,红军西征胜利纪念馆要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,尺寸如图所示(单位:米).(1)求阴影部分的面积(用含x的代数式表示);
(2)当x=8,π取3时,求阴影部分的面积.
 16. 如图,在长方形ABCD中放入一个大正方形AEFG和两个大小相同的小正方形及D,其中、在边BC上,GF与、在同一条直线上且 , 延长交AB于点K,三个阴影部分的面积分别记为、、 , 已知长方形的面积,则下列式子可计算出的是( )
16. 如图,在长方形ABCD中放入一个大正方形AEFG和两个大小相同的小正方形及D,其中、在边BC上,GF与、在同一条直线上且 , 延长交AB于点K,三个阴影部分的面积分别记为、、 , 已知长方形的面积,则下列式子可计算出的是( ) A、 B、 C、 D、
A、 B、 C、 D、四、实践探究题
-
17. 有这样一道题:关于的多项式与的和的值与字母的取值无关,求的值.通常的解题方法是:两式相加后,把看作字母,看作系数合并同类项,因为代数式的值与的取值无关,所以含项的系数为0,即 , 所以 , 则 .

【初步尝试】
(1)若关于的多项式的值与无关,求的值.
【深入探究】
(2)7张如图1的小长方形,长为 , 宽为 , 按照图2方式不重叠地放在大长方形内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为 , 左下角的面积为 .
①若 , 求的值.
②当的长变化时,的值始终保持不变,求与的等量关系.
18. 【方法】有一种整式处理器,能将二次多项式处理成一次多项式,处理方法是:将二次多项式的二次项系数与一次项系数的和(和为非零数)作为一次多项式的一次项系数,将二次多项式的常数项作为一次多项式的常数项.例如: , A经过处理器得到 .
【应用】
若关于x的二次多项式A经过处理器得到B,根据以上方法,解决下列问题:
(1)填空:若 , 则 ;
(2)若 , 求关于x的方程的解;
【延伸】
(3)已知 , M是关于x的二次多项式,若N是M经过处理器得到的整式,满足 , 求m的值.
19. 【综合与实践】如图①是某月份的日历,小乐在其中画出一个的方框(粗线框),框住九个数,然后通过计算探索其中位置如图②所示的四个数“”的值. (1)、初步分析:计算图①中的结果为______.(2)、数学思考:将的方框移动到图①中的其他位置,通过计算可以发现的值均为0.理由如下,请你将其补充完整.
(1)、初步分析:计算图①中的结果为______.(2)、数学思考:将的方框移动到图①中的其他位置,通过计算可以发现的值均为0.理由如下,请你将其补充完整.解:设 , 则 , , ______.
所以( )=______.
(3)、同类探究:利用小乐的方法,借助图①中的日历继续探究,探索其中位置如图③所示的四个数“”的值.写出你的结论,并仿照(2)的方法说明结论成立的理由.20. 若一个两位数的十位和个位上的数学分别为x,y,我们可将这个两位数记为 , 易知 , 同理,一个三位数、四位数等均可以用此记法,如 .[甚础尝试]
(1)填空:
如果要用数字3,6,9组成一个三位数(各数位上的数不同),那么组成的数中最大的三位数是_________;最小的三位数是_________.
[问题探究]
(2)若一个三位数各数位上的数由a,b,c三个数字组成,且 . 那么请说明所组成的最大三位数与最小三位数之差可以被99整除.
[拓展运用]
(3)黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:
①任选一个三位数,要求个、十、百位上的数字各不相同(计算中0可放在百位),把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如:若选的数为729,则),再将这个新数按上述方式重新排列,再相减……这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.该“卡普雷卡尔黑洞数”为_________;
②任意找一个能够被3整除的正整数,先把这个数的每一个数位上的数字都自乘三次(如),所得的值再相加,得到一个新数;然后把这个新数的每一个数位上的数字再自乘三次,所得的值再相加……如此重复运算下去,就能得到一个固定的数_________,我们称它为数字黑洞,T为何具有如此魅力,通过认真的观察、分析,你一定能发现它的奥秘!
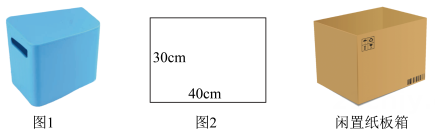
21. 七(1)班数学项目小组为解决小琴奶奶家储物问题,计划将闲置纸板箱制作成储物盒.素材1
如图1,图中是小琴奶奶家需要设置储物盒的区域,该区域可以近似看成一个长方体,底面尺寸如图2所示.
素材2
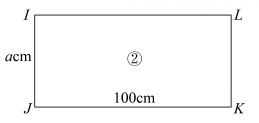
如图是利用闲置纸板箱侧面拆解出的①,②两种宽均为cm(cm)长方形纸板,纸板的厚度忽略不计.
长方形纸板①
长方形纸板②

分别将长方形纸板①和②以不同的方式制作储物盒.
长方形纸板①的制作方式
长方形纸板②制作方式
裁去角上4个相同的小正方形,折成一个无盖长方体储物盒.

将纸片四个角裁去4个相同的小长方形,折成一个有盖的长方体储物盒.
目标1
熟悉材料
按照长方形纸板①的制作方式制成的储物盒能够无缝隙的放入储物区域,则长方形纸板宽为 ▲ cm.
目标2
利用目标1计算所得的数据 , 进行进一步探究.
初步应用
⑴按照长方形纸板①的制作方式,为了更方便地放入或取出储物盒,盒子四周需要留出1cm宽度,求储物盒的容积.
储物收纳
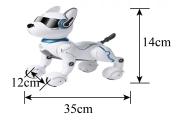
⑵按照长方形纸板②的制作方式制作储物盒,若和两边恰好重合且无重叠部分,如图,是小琴奶奶家里一个玩具机械狗的实物图和尺寸大小,请设计一个各个面均不大于600cm2的储物盒收纳这只玩具狗.
 22. 【综合与实践】
22. 【综合与实践】【知识背景】为丰富市民和游客的文化生活,青秀山举办花灯展.花灯的制作方法主要包括以下步骤:①设计;②选材;③骨架制作;④裱糊(将绸缎等材料粘贴在骨架上);⑤安装灯珠和电路;⑥装饰.
【目标设定】某兴趣小组模仿图1的造型制作花灯.如图2,花灯由4条骨架构成,依次记为 , 每条骨架包括半圆和两条垂直于地面的相等线段.
【步骤实施】的长为2米,半圆的半径为米,完成以下任务(取3).
任务一:求中线段的长;
任务二:如图2所示,与的间距为米,相邻两条骨架的间距由内自外依次递增米,每条骨架的长度如下表所示,请直接写出骨架的长度;
任务三:求裱糊面积(即与地面所围成的图形面积);
任务四:若装饰花灯需要裱糊材料和灯珠盏,在购买材料时有以下两种方案可供选择:
方案1:裱糊材料每平米30元,每盏灯珠10元;
方案2:裱糊材料每平米20元,每盏灯珠15元.
选择哪一种方案更划算?并说明理由.
骨架
骨架的长度(单位:米)
2
▲

五、应用题
-
23. 某电器商销售一种微波炉和电磁炉,微波炉每台定价元,电磁炉每台定价元. “双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁妒都按定价的付款.
现某客户要到该卖场购买微波炉2台,电磁炉台 .
(1)、若该客户按方案一购买,需付款_________元. (用含的代数式表示),若该客户按方案二购买,需付款_________元. (用含的代数式表示)(2)、若时,通过计算说明此时按哪种方案购买较为合算?24. 国庆期间,某超市各个区域都有促销活动,晓琳一家去逛该超市,准备购买纸巾,根据以下素材,探索完成任务.揭秘超市促销:送券和打折哪个更优惠
素材1
纸巾区域推出两种活动:
活动一:购物满100元送30元券,满200元送60元券,…,上不封顶,送的券当天有效,一次性用完.
活动二:所有商品打8折.
注:两种活动不能同时参加.

素材2
晓琳家用的两种纸巾信息(超市标价).

素材3
晓琳家平均三天用1包清风牌纸巾,平均五天用1包4D溶纸巾;晓琳家清风牌纸巾还有1袋存货,4D溶纸巾存货不清楚.
问题解决
任务1
半年(按180天计算),试求出需要消耗清风牌纸巾多少袋?消耗4D溶纸巾多少箱?
任务2
按存半年的量计算,还需要购买2种纸巾,其中4D溶纸巾x箱,若选择活动二,则所需的总费用为______元(用含x的代数式表示).
任务3
晓琳突然想起4D溶纸巾没有存货,按半年所需量,请探索送券和打折哪个更优惠?并写出探索过程.
25. 为了调动学生们体育锻炼的积极性,学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价120元,跳绳每条定价20元.某体育用品商店提供A,B两种优惠方案方案:买一个篮球送一条跳绳;B方案:篮球和跳绳都按定价的付款.已知要购买篮球50个,跳绳条.(1)、若按A方案购买,一共需付款元;若按B方案购买,一共需付款元.(用含的代数式表示)(2)、当时,请通过计算说明此时用哪种方案购买较为合算?(3)、当时,你能给出一种更为省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?26. 如图,现有两摞规格相同的数学课本整齐地叠放在讲台上,请根据图中给出的数据信息,解答下列问题: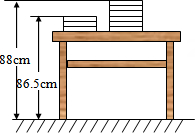 (1)、每本数学课本的厚度为cm,讲台的高度为cm;(2)、当有x本数学课本时,以同样方式叠放在讲台上,高出地面的高度为(用含x的代数式表示);(3)、讲台上有55本数学课本,整齐地叠放成一摞,若有16名同学各从中取走1本,求余下的数学课本高出地面的高度.27. 甲、乙两家体育用品商店出售同样的羽毛球拍和羽毛球,羽毛球拍每副定价25元,羽毛球每盒定价10元.现两家商店搞促销活动,甲店的优惠是:每买一副羽毛球拍赠一盒羽毛球;乙店的优惠是:都按定价的8折出售.某班需购买羽毛球拍4副,羽毛球盒(不小于4).(1)、用代数式表示:若都在甲店购买共需付款多少元,若都在乙店购买共需付款多少元;(2)、当购买羽毛球盒数为12盒时,你能设计出一种更省钱的购买方案吗?试写出你的购买方案,并求出此时需付款多少元?
(1)、每本数学课本的厚度为cm,讲台的高度为cm;(2)、当有x本数学课本时,以同样方式叠放在讲台上,高出地面的高度为(用含x的代数式表示);(3)、讲台上有55本数学课本,整齐地叠放成一摞,若有16名同学各从中取走1本,求余下的数学课本高出地面的高度.27. 甲、乙两家体育用品商店出售同样的羽毛球拍和羽毛球,羽毛球拍每副定价25元,羽毛球每盒定价10元.现两家商店搞促销活动,甲店的优惠是:每买一副羽毛球拍赠一盒羽毛球;乙店的优惠是:都按定价的8折出售.某班需购买羽毛球拍4副,羽毛球盒(不小于4).(1)、用代数式表示:若都在甲店购买共需付款多少元,若都在乙店购买共需付款多少元;(2)、当购买羽毛球盒数为12盒时,你能设计出一种更省钱的购买方案吗?试写出你的购买方案,并求出此时需付款多少元?六、探索规律
-
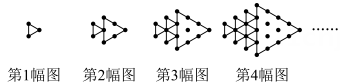
28. 如图所示,将形状、大小完全相同的“•”和线段按照一定规律摆成下列图形.第1 幅图形中“•”的个数为a1 , 第2幅图形中“•”的个数为a2 , 第3幅图形中“•”的个数为a3······依次类推,求 的值.
 29. 如图的图案均是用长度相同的火柴棍按一定的规律拼搭而成的:第1个图案需7根火柴,第2个图案需13根火柴……依此规律,第11个图案需多少根火柴?
29. 如图的图案均是用长度相同的火柴棍按一定的规律拼搭而成的:第1个图案需7根火柴,第2个图案需13根火柴……依此规律,第11个图案需多少根火柴?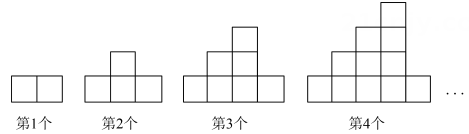 30. 用火柴棒按如图所示的方式搭图形.
30. 用火柴棒按如图所示的方式搭图形. (1)、按图示规律完成下表:
(1)、按图示规律完成下表:图形
1
2
3
4
5
… 火柴棒的根数
5
9
13
… (2)、按照这种方式搭下去,搭第n个图形需要根火柴棒(用含n的式子表示).(3)、小静同学说她按这种方式搭出来的一个图形用了200根火柴棒,你认为可能吗?如果可能,那么该图形是第几个图形?如果不可能,请说明理由.31. 形数(1)、古希腊人常用小石子在沙滩上摆成各种形态来研究数.比如:他们研究过图①中的1,3,6,10,…,由于这些数能够表示成三角形,故将其称为三角形数.类似地,图②中的1,4,9,16,…,这样的数被称为正方形数.下列数中,既是三角形数,又是正方形数的是( ).A、289 B、1024 C、1225 D、1378 (2)、古希腊数学家把数1,3,6,10,15,21,…叫作三角形数,它有一定的规律性,若把第一个三角形数记为a1 , 第二个三角形数记为a2……第n个三角形数记为 an,则有 a3 , a3+a4 , …,请求出a399+a400的值.32. 古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数
(2)、古希腊数学家把数1,3,6,10,15,21,…叫作三角形数,它有一定的规律性,若把第一个三角形数记为a1 , 第二个三角形数记为a2……第n个三角形数记为 an,则有 a3 , a3+a4 , …,请求出a399+a400的值.32. 古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数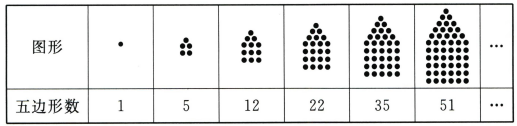
将五边形数1,5,12,22,35,51,…,排成如下数表:

观察这个数表,则这个数表中的第八行从左至右第2个数是多少?