广东省东莞市第四高级中学2024-2025学年高二上学期10月期中考试数学试题
试卷更新日期:2024-11-08 类型:期中考试
一、单项选择题:本题共8小题,每小题5分,共40分.
-
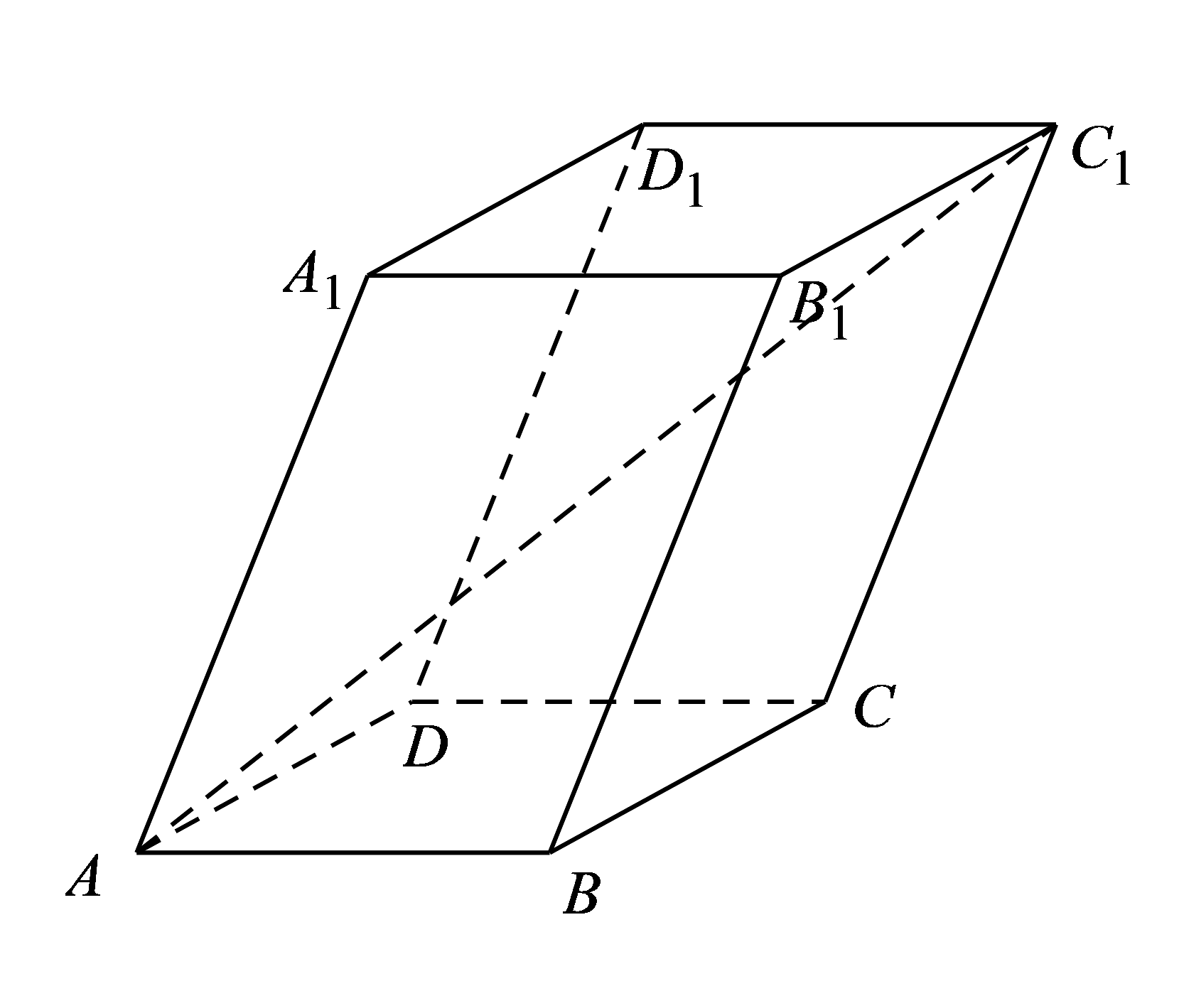
1. 已知点 , 则点A关于x轴对称的点的坐标为( )A、 B、 C、 D、2. 向量 , 若 , 则( )A、 B、 C、 D、3. 已知直线 , 若 , 则( )A、或 B、 C、或 D、4. 直线被圆截得的弦长为( )A、2 B、 C、4 D、5. 如图,平行六面体的底面是边长为1的正方形,且 , , 则线段的长为( )
 A、 B、 C、 D、6. 若方程表示一个圆,则实数 m的取值范围是( )A、 B、 C、 D、7. 人教A版选择性必修二教材的封面图案是斐波那契螺旋线,它被誉为自然界最完美的“黄金螺旋”,自然界存在很多斐波那契螺旋线的图案,例如向日葵、鹦鹉螺等.斐波那契螺旋线的画法是:以斐波那契数1,1,2,3,5,8,…为边长的正方形拼成长方形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.下图为该螺旋线在正方形边长为1,1,2,3,5,8的部分,如图建立平面直角坐标系(规定小方格的边长为1),则接下来的一段圆弧所在圆的方程为( ).
A、 B、 C、 D、6. 若方程表示一个圆,则实数 m的取值范围是( )A、 B、 C、 D、7. 人教A版选择性必修二教材的封面图案是斐波那契螺旋线,它被誉为自然界最完美的“黄金螺旋”,自然界存在很多斐波那契螺旋线的图案,例如向日葵、鹦鹉螺等.斐波那契螺旋线的画法是:以斐波那契数1,1,2,3,5,8,…为边长的正方形拼成长方形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.下图为该螺旋线在正方形边长为1,1,2,3,5,8的部分,如图建立平面直角坐标系(规定小方格的边长为1),则接下来的一段圆弧所在圆的方程为( ).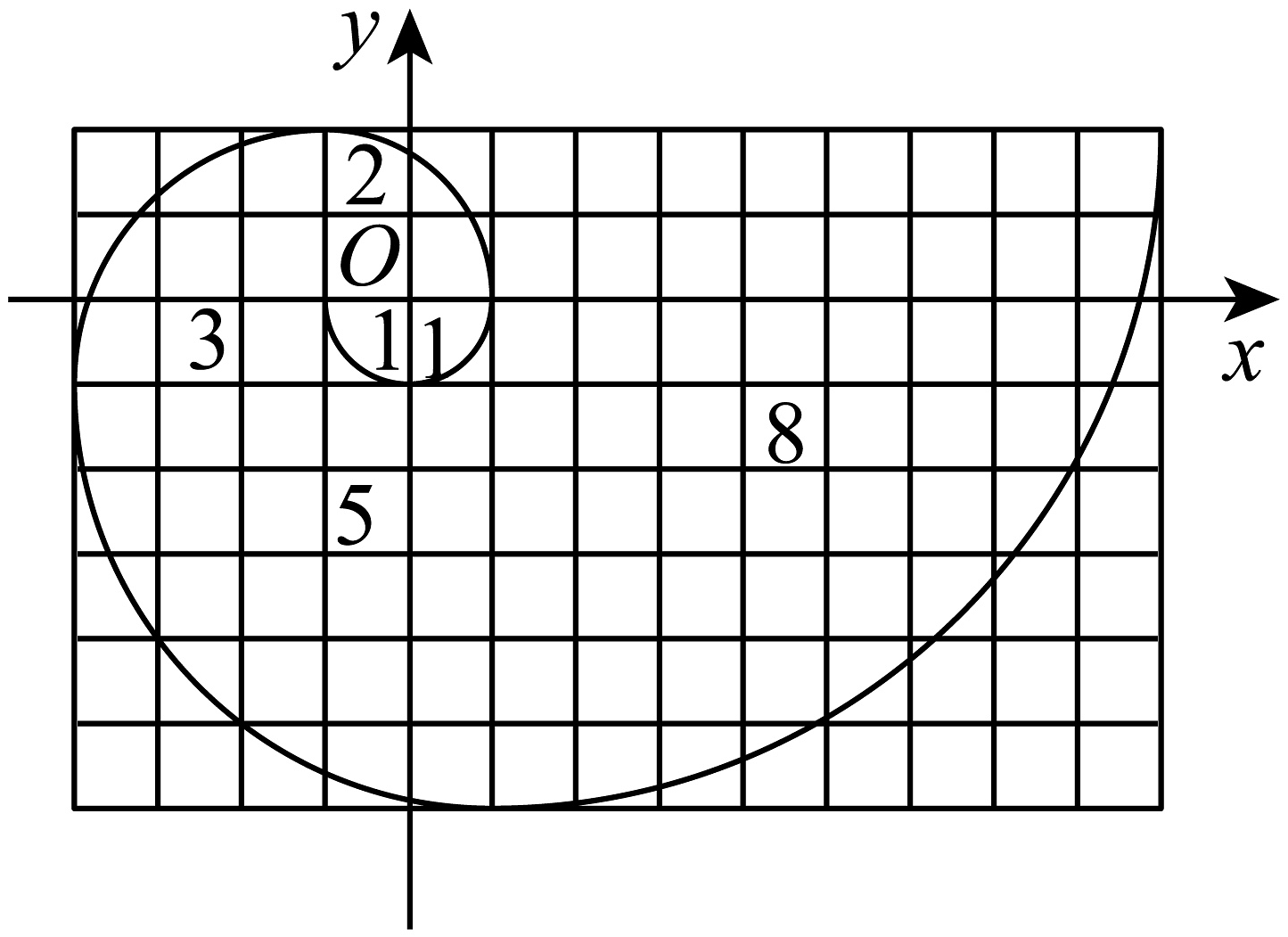 A、 B、 C、 D、8. 在正方体中,分别是棱上的动点,且 , 当、共面时,直线和平面夹角的正弦值为( )
A、 B、 C、 D、8. 在正方体中,分别是棱上的动点,且 , 当、共面时,直线和平面夹角的正弦值为( )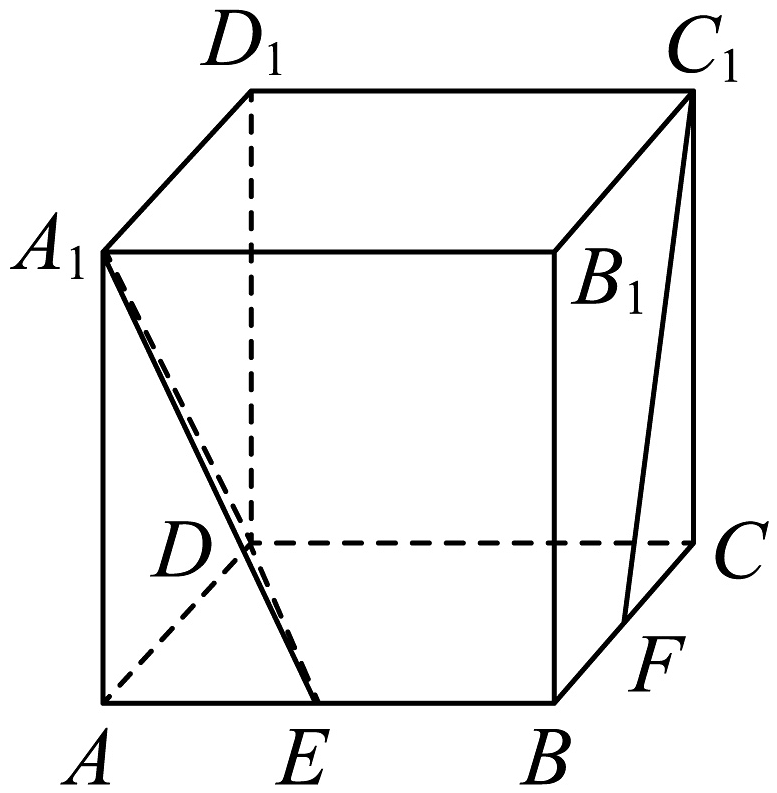 A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 已知圆 , 圆 , 则下列结论正确的是( )A、若和外离,则或 B、若和外切,则 C、当时,有且仅有一条直线与和均相切 D、当时,和内含10. 如图,边长为1的正方形所在平面与正方形在平面互相垂直,动点分别在正方形对角线和上移动,且 , 则下列结论中正确的有( )
 A、 , 使 B、线段存在最小值,最小值为 C、直线与平面所成的角恒为45° D、 , 都存在过且与平面平行的平面
A、 , 使 B、线段存在最小值,最小值为 C、直线与平面所成的角恒为45° D、 , 都存在过且与平面平行的平面三、填空题:本题共3小题,每小题5分,共15分.
-
11. 点到直线的距离为.12. 直线与间的距离为3,则.13. 已知圆: , 圆: , , 分别是圆 , 上的动点,为轴上的动点,则点到 , 两点的距离之和的最小值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
14. 已知空间三点 , 设(1)、求;(2)、若向量与互相垂直,求实数k的值.15. 如图所示,四棱锥的底面是矩形,底面 , , , , .
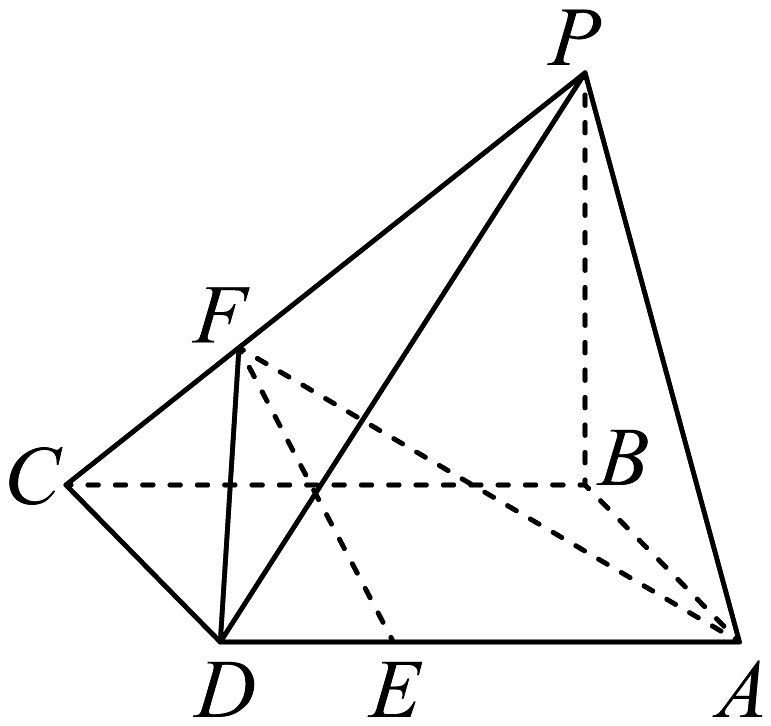 (1)、证明:平面;(2)、求异面直线与所成角的余弦值.
(1)、证明:平面;(2)、求异面直线与所成角的余弦值.