广东省揭阳市普宁市华侨中学2024-2025学年高二上学期11月期中考试数学试题

试卷更新日期：2024-11-10 类型：期中考试

进入出卷网下载

一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合 $A = \{x ∣ x^{2} - 3 x + 2 = 0\}, B = {x ∣ x - 4 < 0}$ ，则 $A \cap B =$ （）

A、 $\emptyset$ B、 $\{1\}$ C、 $\{2\}$ D、 $\{1, 2\}$

查看试题解析
2. 已知复数 $z$ 满足 $(1 + i) z = 2 + 4 i$ ，则复数 $|z|$ 等于（）

A、1 B、 $\sqrt{2}$ C、3 D、 $\sqrt{10}$

查看试题解析
3. 已知直线 $l_{1} : a x + 3 y - 5 = 0$ 与 $l_{2} : (3 a - 2) x + a y + 4 = 0$ 垂直，则 $a =$ （）

A、0 B、0或 $- \frac{1}{3}$ C、 $- \frac{1}{3}$ D、0或 $\frac{2}{3}$

查看试题解析
4. 在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $E, F$ 分别是 $B C, C C_{1}$ 的中点， $\vec{A G} = 2 \vec{G E}$ ，则 $\vec{F G} =$ （）

A、 $\frac{1}{3} \vec{A B} - \frac{2}{3} \vec{A C} - \frac{1}{2} \vec{A A_{1}}$ B、 $\frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C} + \frac{1}{2} \vec{A A_{1}}$ C、 $- \frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A C} - \frac{1}{2} \vec{A A_{1}}$ D、 $- \frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C} + \frac{1}{2} \vec{A A_{1}}$

查看试题解析
5. 已知圆 $C_{1} : x^{2} + y^{2} - 2 x + m y + 1 = 0 (m \in R)$ 的面积被直线 $x + 2 y + 1 = 0$ 平分，圆 $C_{2} : {(x + 2)}^{2} + {(y - 3)}^{2} = 16$ ，则圆 $C_{1}$ 与圆 $C_{2}$ 的位置关系是（）

A、外离 B、相交 C、内切 D、外切

查看试题解析
6. 为了研究我市甲、乙两个 $5 G$ 智能手机专卖店的销售状况，厂家统计了去年4月到9月甲、乙两店每月的营业额（单位：万元），得到如图所示的折线图．根据两店的营业额折线图可知，下列说法错误的是（）

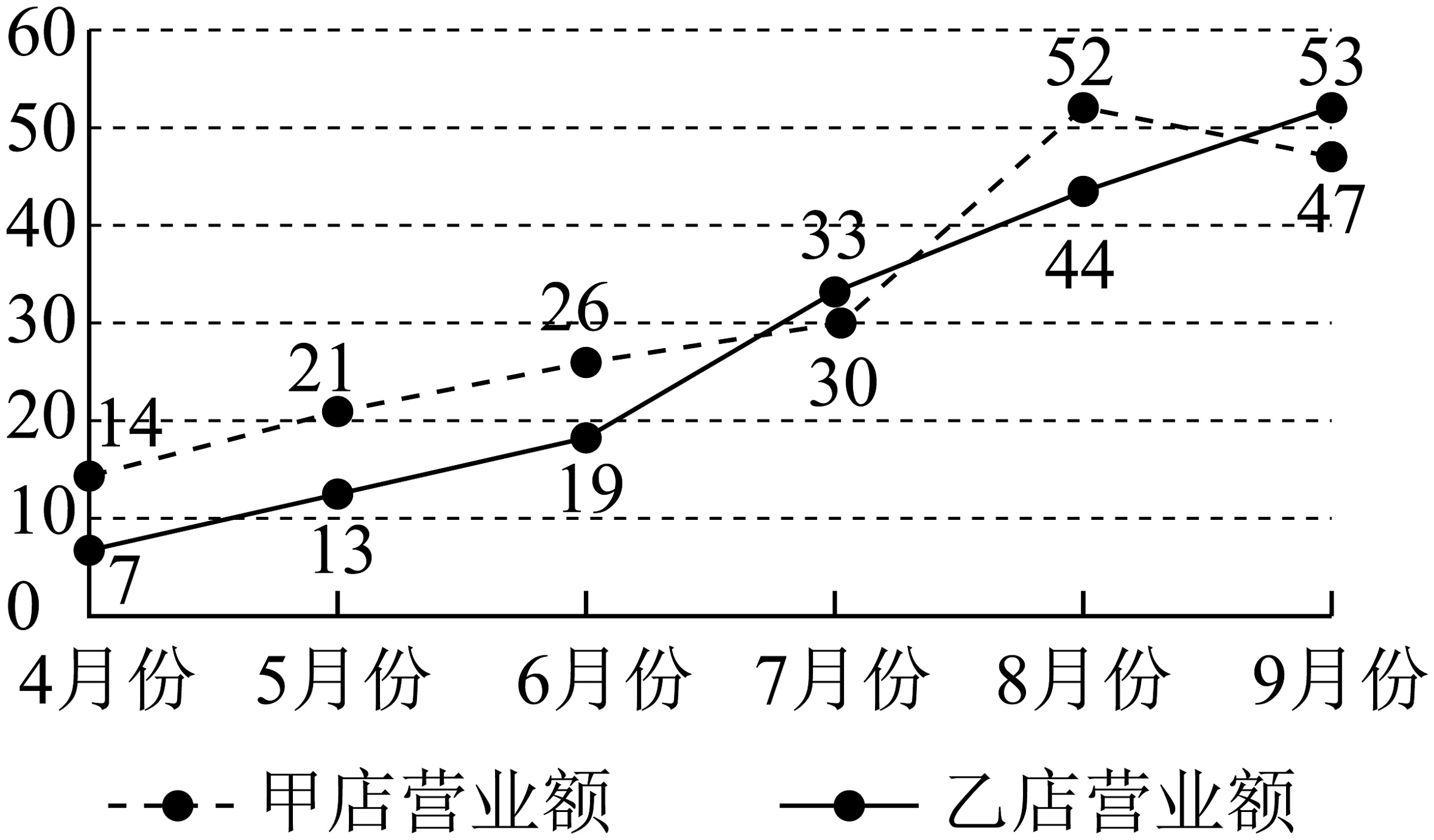A、甲店月营业额的平均值在 $[31, 32]$ 内 B、乙店月营业额总体呈上升趋势 C、7、8、9月份的总营业额甲店比乙店少 D、乙店的月营业额极差小于甲店的月营业额极差

查看试题解析
7. 已知直线 $l$ 恒过点 $(0, 5)$ ，圆 $C : {(x - 3)}^{2} + y^{2} = 9$ ，则“直线 $l$ 的斜率为 $- \frac{8}{15}$ ”是“直线 $l$ 与圆 $C$ 相切”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
8. 在 $△ A B C$ 中，点 $D$ 是边 $B C$ 上一点，若 $\vec{A D} = x \vec{A B} + y \vec{A C}$ ，则 $\frac{2 x + 5 y}{x y}$ 的最小值为（）

A、 $7 - 2 \sqrt{10}$ B、 $7 + 2 \sqrt{10}$ C、 $- 2 \sqrt{10}$ D、7

查看试题解析

二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. 下列命题说法正确的有（）

A、已知直线 $l_{1}$ ： $m x + 2 y - 2 = 0$ 与直线 $l_{2}$ ： $5 x + (m + 3) y - 5 = 0$ ，若 $l_{1} / / l_{2}$ ，则 $m = 2$ 或 $m = - 5$ B、点 $(5, 0)$ 关于直线 $y = x + 1$ 的对称点的坐标为 $(- 1, 6)$ C、直线 $k x + (k + 1) y - 3 k - 1 = 0$ 过定点 $(2, 1)$ D、过点 $P (1, 2)$ 且在 $x$ 轴， $y$ 轴上的截距相等的直线方程为 $x + y - 3 = 0$

查看试题解析
10. 已知向量 $\vec{a} = (1, 1, 0), \vec{b} = (0, 1, 1), \vec{c} = (1, 2, 1)$ ，则下列结论正确的是（）

A、向量 $\vec{a}$ 与向量 $\vec{b}$ 的夹角为 $\frac{π}{3}$ B、 $\vec{c} ⊥ (\vec{a} - \vec{b})$ C、向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量为 $(\frac{1}{2}, 0, \frac{1}{2})$ D、向量 $\vec{c}$ 与向量 $\vec{a}, \vec{b}$ 共面

查看试题解析
11. 函数 $f (x) = A \sin (ω x + φ) (A > 0, ω > 0.0 < φ < \frac{π}{2})$ 的部分图象如图所示，则下列说法正确的是（）

A、 $f (x) = 2 \sin (2 x + \frac{π}{6})$ B、 $f (x)$ 的一个单调递增区间为 $[\frac{11 π}{6}, \frac{7 π}{3}]$ C、函数 $f (x)$ 的图象关于点 $(- \frac{7 π}{12}, 0)$ 对称 D、若函数 $f (λ x) (λ > 0)$ 在 $[0, π]$ 上没有零点，则 $λ \in (0, \frac{5}{12})$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分.

12. 已知直线 $x + 2 y + 1 = 0$ 与 $⊙ C : {(x - 1)}^{2} + y^{2} = 4$ 交于 $A$ ， $B$ 两点，则 $△ A B C$ 的面积为.

查看试题解析
13. 已知 $tan α = 2$ ，则 $\frac{sin α + cos α}{sin α - cos α} =$ .

查看试题解析
14. 《九章算术》是我国古代内容极为丰富的数学名著.该书中有如下问题：“今有委米依垣内角，下周六尺，高四尺.问：积及委米几何?”其意思：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为6尺，米堆的高为4尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.6立方尺，圆周率约为3，估算堆放的米约有斛.

查看试题解析

四、解答题：本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤.

15. 在 $△ A B C$ 中，角A，B，C的对边分别为a，b， $c$ ，已知 $b \cos C = (4 a - c) \cos B$ ．

(1)、求 $\cos B$ ；

(2)、若 $a = 4, △ A B C$ 的面积为 $\sqrt{15}$ ，求 $△ A B C$ 的周长．

查看试题解析
16. 已知直线 $2 x - 3 y + 1 = 0$ 和直线 $x + y - 2 = 0$ 的交点为 $P$ .

(1)、求过点 $P$ 且与直线 $3 x - y - 1 = 0$ 平行的直线方程；

(2)、若直线 $l_{1}$ 与直线 $3 x - y - 1 = 0$ 垂直，且 $P$ 到 $l_{1}$ 的距离为 $\frac{\sqrt{10}}{5}$ ，求直线的方程.

查看试题解析
17. 中学阶段是学生身体发育最重要的阶段，长时间熬夜学习严重影响学生的身体健康．某校为了解甲、乙两班学生每周自我熬夜学习的总时长（单位：小时），分别从这两个班中随机抽取5名同学进行调查，得到他们最近一周自我熬夜学习的总时长的样本数据：
甲班
8
13
28
32
39
乙班
12
25
26
28
31
如果学生平均每周自我熬夜学习的总时长超过26小时，则称为“过度熬夜”．

(1)、请根据样本数据，分别估计甲、乙两班的学生平均每周自我熬夜学习时长的平均值；

(2)、从样本甲、乙两班所有“过度熬夜”的学生中任取2人，求这2人都来自甲班的概率．

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中， $P A ⊥$ 底面 $A B C D$ ， $B C //$ 平面 $P A D$ ， $B C ⊥ A B$ .

(1)、证明： $A D ⊥$ 平面 $P A B$ .

(2)、若 $A D = A B$ ， $P A = B C$ ，且直线 $P D$ 与直线 $B C$ 所成角的正切值为 $\frac{3}{2}$ ，求二面角 $A - C D - P$ 的余弦值.

查看试题解析
19. 如图1，已知圆心 $C$ 在 $x$ 轴的圆 $C$ 经过点 $D (3, 0)$ 和 $E (2, \sqrt{3})$ .过原点且不与 $x$ 铀重合的直线 $l$ 与圆 $C$ 交于A、B两点（ $A$ 在 $x$ 轴上方）.

(1)、求圆 $C$ 的标准方程；

(2)、若 $△ A B D$ 的面积为 $\sqrt{11}$ ，求直线l的方程；

(3)、将平面xOy沿 $x$ 轴折叠，使 $y$ 轴正半轴和 $x$ 轴所确定的半平面（平面AOD)与y轴负半轴和 $x$ 轴所确定的半平面（平面BOD）互相垂直，如图2，求折叠后 $|A B|$ 的范围.

查看试题解析

甲班	8	13	28	32	39
乙班	12	25	26	28	31