浙江省金砖联盟2024-2025学年高二上学期期中联考数学试题
试卷更新日期:2024-11-20 类型:期中考试
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.
-
1. 在空间直角坐标系中,点关于轴的对称点的坐标为( )A、 B、 C、 D、2. 已知平面 , , 直线 , 且 , 则“”是“∥”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 已知复数满足 , 则( )A、 B、 C、 D、4. 已知 , 两直线 , 若 , 则的最小值为( )A、12 B、20 C、26 D、325. 已知甲罐中有四个相同的小球,标号为 , 乙罐中有三个相同的小球,标号为 , 从甲罐,乙罐中分别随机抽取1个小球,记事件“抽取的两个小球标号之和大于6”,事件“抽取的两个小球标号之积小于6”,则下列说法错误的是( )A、事件发生的概率为 B、事件相互独立 C、事件是互斥事件 D、事件发生的概率为6. 当圆截直线所得的弦长最短时,实数( )A、-1 B、 C、1 D、7. 八卦是中国文化的基本学概念,图1是八卦模型图,其平面图形为图2所示的正八边 , 其中给出下列结论,其中正确的结论为( )
 A、与的夹角为 B、 C、 D、在上的投影向量为(其中为与同向的单位向量)8. 已知锐角 , 角的对边分别 , 且 , 则的取值范围是( )A、 B、 C、 D、
A、与的夹角为 B、 C、 D、在上的投影向量为(其中为与同向的单位向量)8. 已知锐角 , 角的对边分别 , 且 , 则的取值范围是( )A、 B、 C、 D、二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.
-
9. 已知甲组数据为: , 乙组数据为: , 则下列说法正确的是( )A、这两组数据的第80百分位数相等 B、这两组数据的极差相等 C、这两组数据分别去掉一个最大值和一个最小值后,均值都不变 D、甲组数据比乙组数据分散10. 已知椭圆 , 点为椭圆两焦点,点为椭圆上的动点,过点作的外角平分线 , 过椭圆的焦点作直线的垂线,垂足是.现有一条长度为4的线段在直线上运动,且始终满足为锐角,则( )A、点的轨迹方程是 B、点有可能在以为直径的圆上 C、点不可能在直线上 D、线段的中点的纵坐标的取值范围是11. 如图,在棱长为1的正方体中,为棱的中点,为正方形内一动点(含边界),则下列说法中正确的是( )
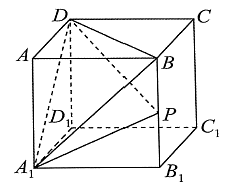 A、直线平面 B、三棱锥的外接球的表面积为 C、直线与直线所成角的正弦值为 D、若 , 那么点的轨迹长度为
A、直线平面 B、三棱锥的外接球的表面积为 C、直线与直线所成角的正弦值为 D、若 , 那么点的轨迹长度为三、填空题:本题共3小题,每小题5分,共15分.
-
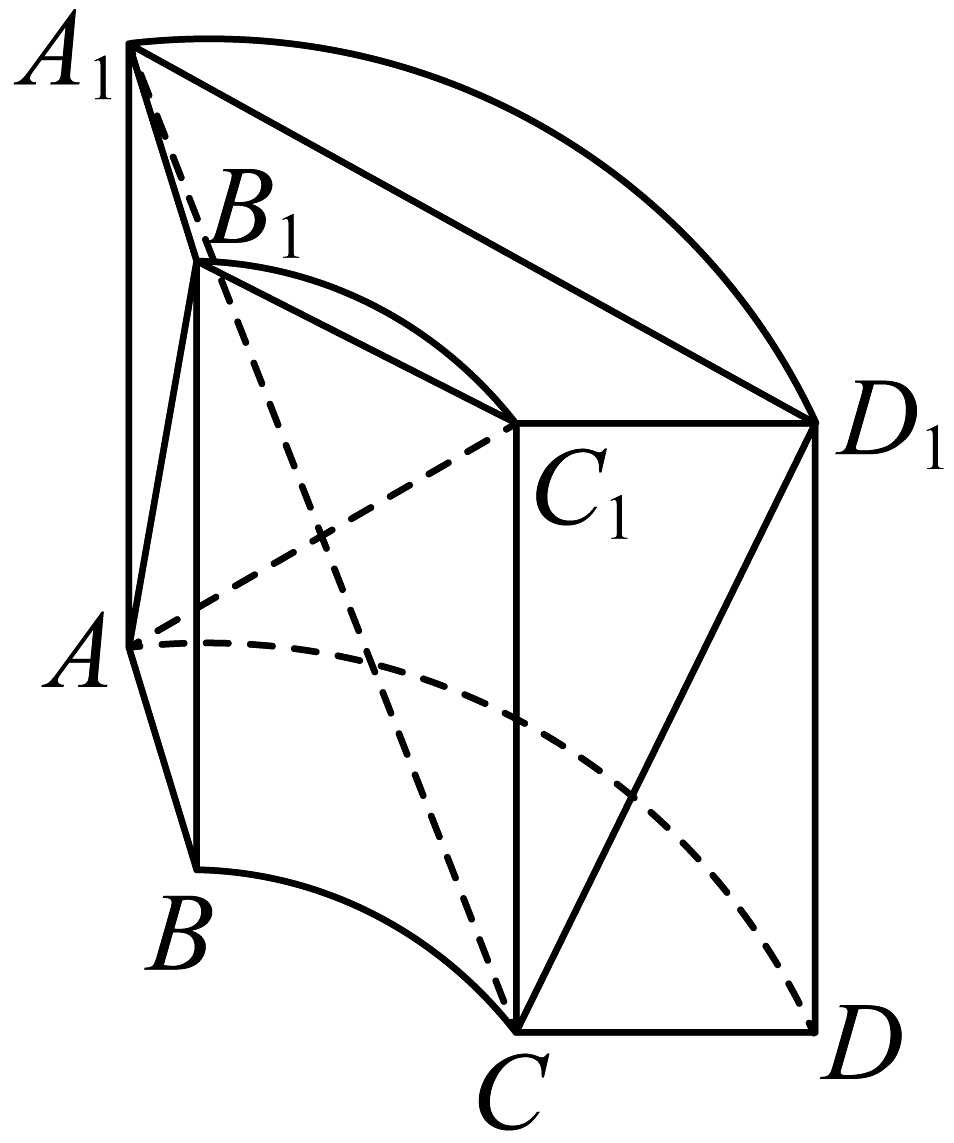
12. 若直线的一个方向向量 , 则的倾斜角大小为 .13. 中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分),现有一个如图所示的曲池,它的高为2,均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为 , 则图中平面与平面所成角的余弦值为.
 14. 设双曲线的右焦点是 , 左、右顶点分别是 , 过作轴的垂线交双曲线于两点,若 , 则双曲线的离心率为 .
14. 设双曲线的右焦点是 , 左、右顶点分别是 , 过作轴的垂线交双曲线于两点,若 , 则双曲线的离心率为 .四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
-
15. 为提高服务质量,某社区居委会进行了居民对社区工作满意度的问卷调查.随机抽取了100户居民的问卷进行评分统计,评分的频率分布直方图如图所示,数据分组依次为:
 (1)、求的值;(2)、求这100户居民问卷评分的中位数;(3)、若根据各组的频率的比例采取分层抽样的方法,从评分在和内的居民中共抽取6户居民,查阅他们答卷的情况,再从这6户居民中选取4户进行专项调查,求这4户居民中恰有1户的评分在内的概率.16. 在中,角的对边分别为 , 且 .(1)、求角的大小;(2)、若 , 角的平分线交于点 , 求线段的长.17. 如图在四棱锥中, , , , , , 是的中点.
(1)、求的值;(2)、求这100户居民问卷评分的中位数;(3)、若根据各组的频率的比例采取分层抽样的方法,从评分在和内的居民中共抽取6户居民,查阅他们答卷的情况,再从这6户居民中选取4户进行专项调查,求这4户居民中恰有1户的评分在内的概率.16. 在中,角的对边分别为 , 且 .(1)、求角的大小;(2)、若 , 角的平分线交于点 , 求线段的长.17. 如图在四棱锥中, , , , , , 是的中点.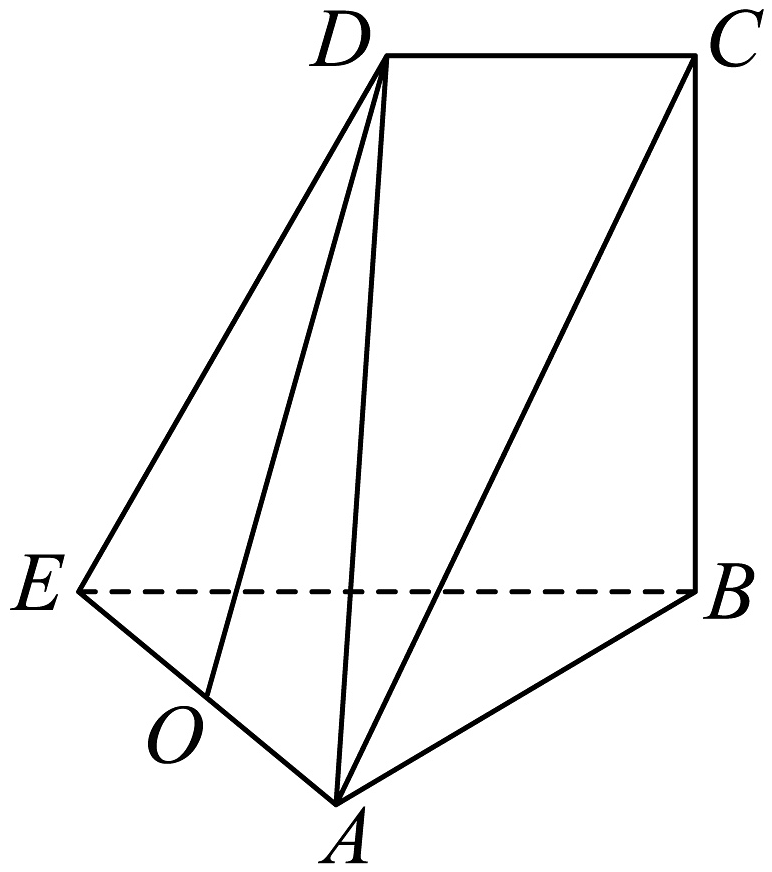 (1)、求证:平面;(2)、在棱上是否存在点 , 使得直线与平面所成角的正弦值为 , 若存在,求的值,若不存在,说明理由18. 如图,已知圆为坐标原点,过点作直线交圆于点 , 过点分别作圆的切线,两条切线相交于点 .
(1)、求证:平面;(2)、在棱上是否存在点 , 使得直线与平面所成角的正弦值为 , 若存在,求的值,若不存在,说明理由18. 如图,已知圆为坐标原点,过点作直线交圆于点 , 过点分别作圆的切线,两条切线相交于点 . (1)、若直线的斜率为1,求的值;(2)、求点的轨迹方程;(3)、若两条切线与轴分别交于点 , 求的最小值.19. 已知椭圆的左、右焦点分别为 , 离心率为 , 经过点且倾斜角为的直线与椭圆交于两点(其中点在轴上方),的周长为8.
(1)、若直线的斜率为1,求的值;(2)、求点的轨迹方程;(3)、若两条切线与轴分别交于点 , 求的最小值.19. 已知椭圆的左、右焦点分别为 , 离心率为 , 经过点且倾斜角为的直线与椭圆交于两点(其中点在轴上方),的周长为8.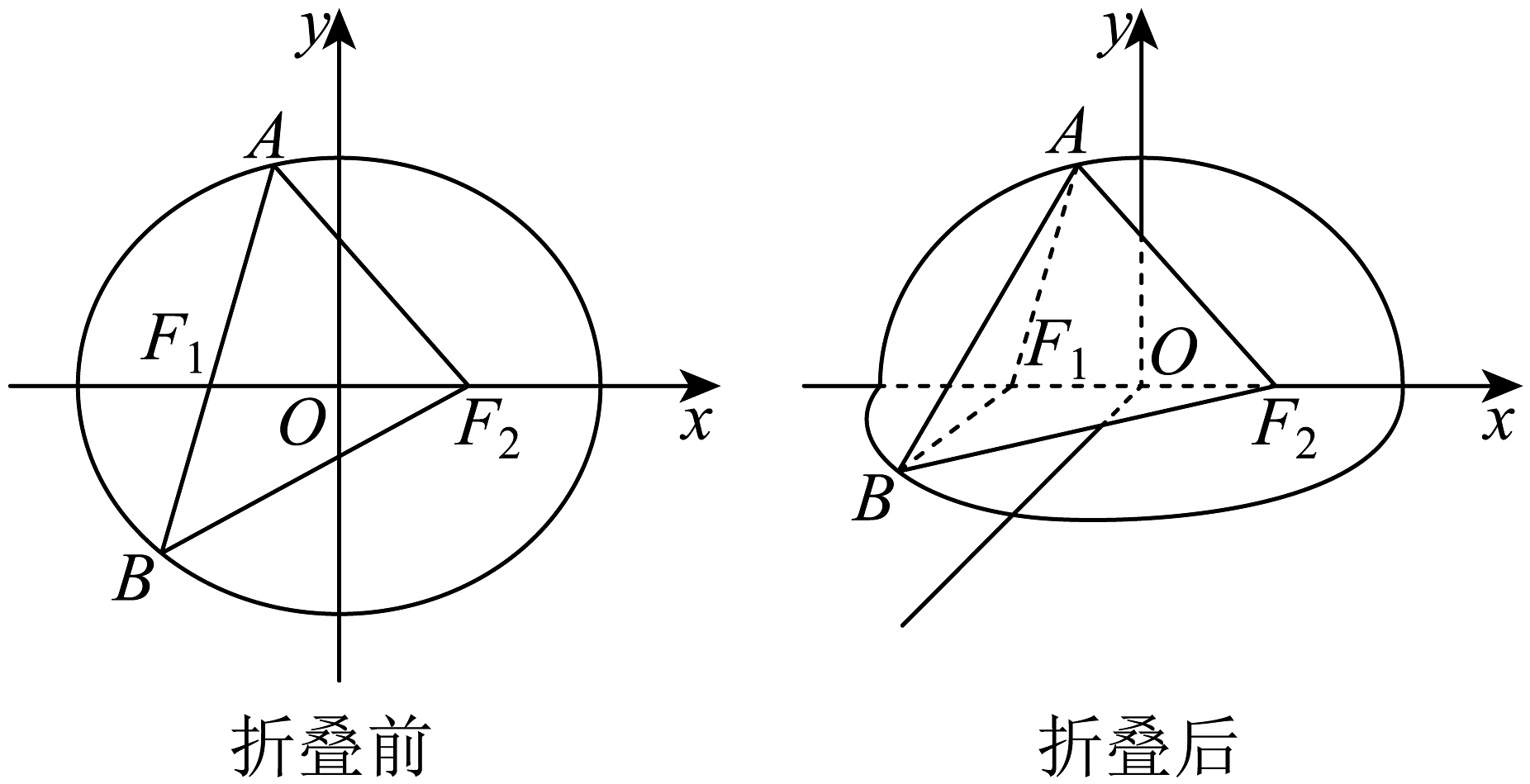 (1)、求椭圆的标准方程;(2)、如图,将平面沿轴折叠,使轴正半轴和轴所确定的半平面(平面)与轴负半轴和轴所确定的半平面(平面)互相垂直.
(1)、求椭圆的标准方程;(2)、如图,将平面沿轴折叠,使轴正半轴和轴所确定的半平面(平面)与轴负半轴和轴所确定的半平面(平面)互相垂直.①若 , 求三棱锥的体积;
②是否存在 , 使得折叠后的周长为与折叠前的周长之比为?若存在,求的值;若不存在,请说明理由.