广东省惠州市2024-2025学年高三第二次调研考试（期中）数学试题

试卷更新日期：2024-11-05 类型：期中考试

进入出卷网下载

一、单项选择题：本题共8小题，每小题满分5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分.

1. 已知集合 $A = \{x ∣ 2 \leq x < 5\}$ ，集合 $B = \{x ∣ x^{2} - 4 x < 0\}$ ，则 $A \cap B =$ （）

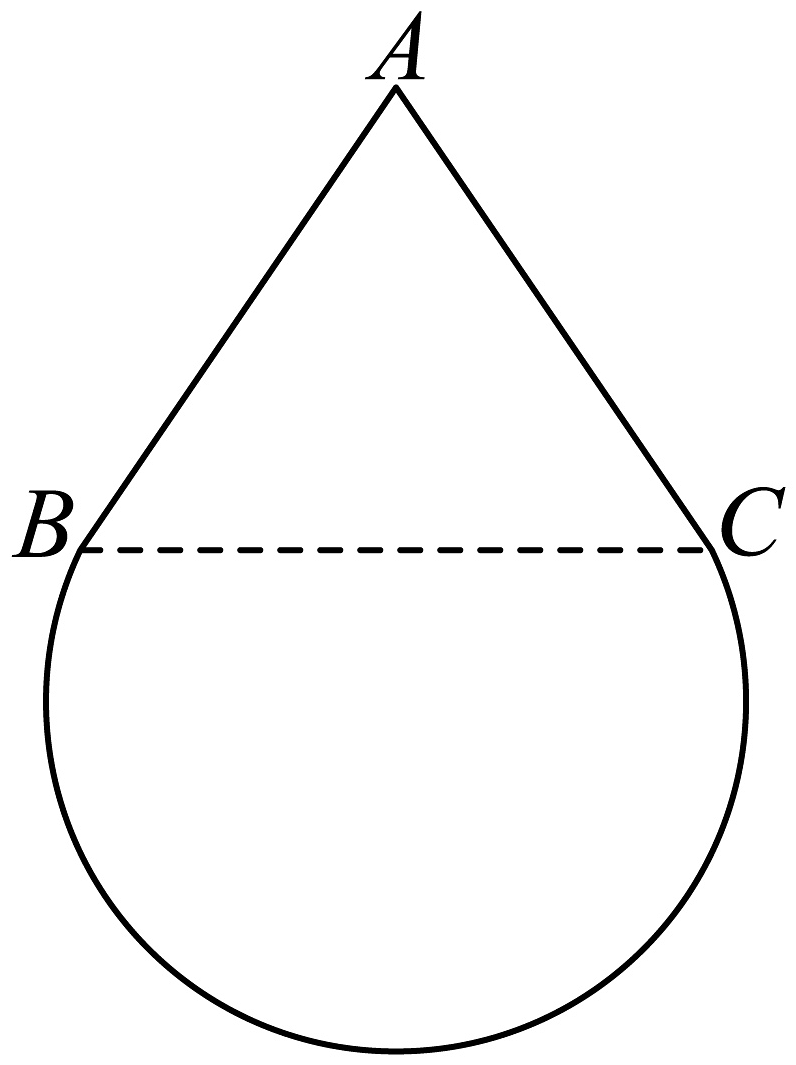
A、 $(0, 5)$ B、 $[2, 4)$ C、 $(4, 5)$ D、 $(- \infty, 0) \cup [2, + \infty)$

查看试题解析
2. 已知复数z满足 $z^{2} + 1 = 0$ ，则 $|z + 1| =$ （）

A、3 B、2 C、 $\sqrt{2}$ D、1

查看试题解析
3. 已知等差数列{a_n}前9项的和为27，a₁₀=8，则a₁₀₀=（　　）

A、100 B、99 C、98 D、97

查看试题解析
4. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，棱 $B C, A_{1} B_{1}$ 的中点分别为 $E$ ， $F$ ，则直线 $E F$ 与平面 $A B B_{1} A_{1}$ 所成角的正弦值为（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{6}}{6}$ D、 $\frac{\sqrt{30}}{6}$

查看试题解析
5. 已知向量 $\vec{a}, \vec{b}$ 满足： $\vec{a} = (\sqrt{3}, 1), |\vec{b}| = \sqrt{2}, (2 \vec{a} - \vec{b}) \cdot \vec{b} = 3$ ，则向量 $\vec{b}$ 在向量 $\vec{a}$ 上的投影向量为（）

A、 $(\frac{5 \sqrt{3}}{8}, \frac{5}{8})$ B、 $(\frac{5 \sqrt{3}}{4}, \frac{5}{4})$ C、 $(\frac{\sqrt{3}}{8}, \frac{1}{8})$ D、 $(\frac{\sqrt{3}}{4}, \frac{1}{4})$

查看试题解析
6. 已知函数 $f (x) = {log}_{2} (x^{2} - 2 a x), a \in R$ ，则“ $a \leq 0$ ”是“函数 $f (x)$ 在 $(1, + \infty)$ 上单调递增”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
7. 已知“水滴”的表面是一个由圆锥的侧面和部分球面（常称为“球冠”）所围成的几何体.如图所示，将“水滴”的轴截面看成由线段 $A B, A C$ 和优弧 $B C$ 所围成的平面图形，其中点 $B, C$ 所在直线与水平面平行， $A B$ 和 $A C$ 与圆弧相切.已知“水滴”的“竖直高度”与“水平宽度”（“水平宽度”指的是平行于水平面的直线截轴截面所得线段的长度的最大值）的比值为 $\frac{4}{3}$ ，则 $sin ∠ B A C =$ （）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{16}{25}$ D、 $\frac{24}{25}$

查看试题解析
8. 在统计某学校所有选择理科和文科的学生数据中，发现理科生多于文科生，女生多于男生，则关于本次学生样本的数据中，结论一定成立的是（）

A、理科男生多于文科女生 B、文科女生多于文科男生 C、理科女生多于文科男生 D、理科女生多于理科男生

查看试题解析

二、多选题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. 某公司为保证产品生产质量，连续10天监测某种新产品生产线的次品件数，得到关于每天出现的次品的件数的一组样本数据： $3, 4, 3, 1, 5, 3, 2, 5, 1, 3$ .则关于这组数据的结论正确的是（）

A、极差是4 B、众数小于平均数 C、方差是2 D、数据的第80百分位数为4.5

查看试题解析
10. 函数 $f (x) = A sin (ω x + φ) (A > 0, ω > 0, |φ| < \frac{π}{2})$ 的部分图象如图所示，现将 $f (x)$ 的图象向左平移 $\frac{π}{6}$ 个单位长度，得到函数 $g (x)$ 的图象，则下列结论正确的是（）

A、 $φ = - \frac{π}{6}$ B、 $ω = 2$ C、函数 $y = x f (x + \frac{π}{12})$ 是奇函数 D、 $g (x) = 2 cos (2 x - \frac{π}{3})$

查看试题解析
11. 如图，心形曲线 $L : x^{2} + {(y - |x|)}^{2} = 1$ 与 $y$ 轴交于 $A, B$ 两点，点 $P$ 是 $L$ 上的一个动点，则（）

A、点 $(\frac{\sqrt{2}}{2}, 0)$ 和 $(- 1, 1)$ 均在 $L$ 上 B、点 $P$ 的纵坐标的最大值为 $\sqrt{2}$ C、 $|O P|$ 的最大值与最小值之和为3 D、 $|P A| + |P B| \leq 2 \sqrt{3}$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分.

12. 在 ${(x + 1)}^{5}$ 的二项展开式中，各项的系数和为.

查看试题解析
13. 椭圆 $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F₁ ， F₂ ．若|AF₁|，|F₁F₂|，|F₁B|成等比数列，则此椭圆的离心率为．

查看试题解析
14. 若关于 $x$ 的方程 $ln (a x + \frac{b}{2}) = \sqrt{x^{2} + \frac{1}{4}}$ 有实根，则 $a^{2} + b^{2}$ 的最小值为.

查看试题解析

四、解答题：本题共5小题，共77分.解答应写出必要的文字说明､证明过程或演算步骤.

15. 已知函数 $f (x) = \frac{1}{2} x^{2} - x - 2 \ln x$ ．

(1)、求曲线 $y = f (x)$ 在点 $(1, f (1))$ 处的切线方程；

(2)、求函数 $f (x)$ 在区间 $[1, e]$ 上的最小值．

查看试题解析
16. 如图，四棱锥 $P - A B C D$ 中， $P A ⊥$ 底面 $A B C D, A B$ $∥$ $C D, A D = C D = 1$ ， $∠ B A D = 120^{\circ}, ∠ A C B = 90^{\circ}$ .

(1)、求证： $B C ⊥$ 平面 $P A C$ ；

(2)、若 $P A = \sqrt{3}$ ，求平面 $P C D$ 与平面 $P C A$ 夹角的余弦值.

查看试题解析
17. 已知双曲线 $C : x^{2} - y^{2} = 1$ 及直线 $l : y = k x - 1$ .

(1)、若 $l$ 与 $C$ 有两个不同的交点，求实数 $k$ 的取值范围；

(2)、若 $l$ 与 $C$ 交于 $A, B$ 两点， $O$ 是坐标原点，且 $△ O A B$ 的面积为 $\sqrt{2}$ ，求实数 $k$ 的值.

查看试题解析
18. 记 $△ A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ，已知 $a < b < c$ 且 $tan A, tan B, tan C$ 均为整数.

(1)、求 $tan A, tan B, tan C$ 的值；

(2)、设 $A C$ 的中点为 $D$ ，求 $∠ C D B$ 的余弦值.

查看试题解析
19. 若数列 $\{a_{n}\} (1 \leq n \leq k, n \in N^{*}, k \in N^{*})$ 满足 $a_{n} \in \{0, 1\}$ ，则称数列 $\{a_{n}\}$ 为 $k$ 项 $0 - 1$ 数列，由所有 $k$ 项 $0 - 1$ 数列组成集合 $M_{k}$ .

(1)、若 $\{a_{n}\}$ 是12项0 $- 1$ 数列，当且仅当 $n = 3 p (p \in N^{*}, p \leq 4)$ 时， $a_{n} = 0$ ，求数列 $\{{(- 1)}^{n} a_{n}\}$ 的所有项的和；

(2)、从集合 $M_{k}$ 中任意取出两个数列 $\{a_{n}\}, \{b_{n}\}$ ，记 $X = \sum_{i = 1}^{k} |a_{i} - b_{i}|$ .
①求随机变量 $X$ 的分布列，并证明： $E (X) > \frac{k}{2}$ ；
②若用某软件产生 $k (k \geq 2)$ 项 $0 - 1$ 数列，记事件 $A =$ “第一次产生数字1”， $B =$ “第二次产生数字1”，且 $0 < P (A) < 1, 0 < P (B) < 1$ .若 $P (B ∣ A) < P (B ∣ \bar{A})$ ，比较 $P (A ∣ B)$ 与 $P (A ∣ \bar{B})$ 的大小.

查看试题解析