广东省深圳市罗湖区2024-2025学年高三上学期期末质量检测数学试题

试卷更新日期：2025-01-18 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 设集合 $A = {x \in R ∣ \sqrt{x} < 4}, B = {0, 1, 4, 9, 16}$ ，则 $A \cap B =$ （）

A、 ${0, 1}$ B、 ${0, 1, 4}$ C、 ${0, 1, 4, 9}$ D、 ${1, 4, 9, 16}$

查看试题解析
2. 若复数 $z$ 满足 $z (1 - i) = 1 + i$ ，则 $z^{4} =$ （）

A、1 B、-1 C、 $i$ D、16

查看试题解析
3. ${(x + \frac{1}{\sqrt{x}})}^{6}$ 的展开式中常数项为（）

A、5 B、10 C、15 D、20

查看试题解析
4. 已知样本 $x_{1}, x_{2}, \dots, x_{7}$ 的标准差为2，平均数为3，则 $x_{1}^{2} + x_{2}^{2} + \dots + x_{7}^{2}$ 值为（）

A、35 B、77 C、49 D、91

查看试题解析
5. 当 $n \in Z, x \in [n, n + 1)$ ，定义 $[x] = n$ ，则 $f (x) = x - [x], x \in R$ 为（）

A、周期函数 B、奇函数 C、偶函数 D、单调递增函数

查看试题解析
6. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上一点A关于原点的对称点为点B，F为其右焦点，若 $A F ⊥ B F (| A F | < | B F |)$ ，且离心率为 $\frac{\sqrt{6}}{3}$ ，则 $∠ A B F =$ （）

A、 $\frac{π}{12}$ B、 $\frac{5 π}{12}$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析
7. 已知圆 $C : {(x - 1)}^{2} + {(y - 2)}^{2} = 4$ ，直线 $l : (a + 1) x + (2 a - 2) y - 4 a = 0$ ，若直线l与圆C两交点记为A，B，点P为圆C上一动点，且满足 $C P ∥ A B$ ，则 $\vec{P A} \cdot \vec{P B}$ 最大值为（）

A、 $2 \sqrt{2}$ B、3 C、4 D、8

查看试题解析
8. 已知向量 $\vec{a}$ 、 $\vec{b}$ 满足 $|\vec{a}| = 2, |2 \vec{a} + \vec{b}| - |\vec{b}| = 2$ ，则 $|\vec{a} + \vec{b}|$ 的取值范围是（）

A、 $[0, 1]$ B、 $[1, + \infty)$ C、 $[1, 2]$ D、 $[\frac{1}{2}, + \infty)$

查看试题解析

二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $\vec{A M} = λ \vec{A A_{1}}, \vec{C N} = λ \vec{C C_{1}} (0 \leq λ \leq 1)$ ，下列说法正确的是（）

A、 $M N / /$ 平面 $A B C D$ B、 $B D ⊥ M N$ C、存在λ，使得 $C M ⊥ D_{1} N$ D、当 $λ = \frac{1}{3}$ 时，平面 $D_{1} M N$ 截正方体的表面所得的图形为五边形

查看试题解析
10. 已知函数 $f (x) = \sin (ω x + \frac{3 π}{4}) (ω > 0)$ ，下列说法正确的是（）

A、当 $ω = 2$ 时， $f (x)$ 的图象关于直线 $x = - \frac{π}{8}$ 对称 B、当 $ω = 2$ 时，将 $f (x)$ 的图象向左平移 $\frac{π}{4}$ 个单位得到 $g (x)$ ， $g (x)$ 的图象关于原点对称 C、当 $ω = 1$ 时， $f (x)$ 在 $[\frac{π}{4}, \frac{π}{2}]$ 单调递减 D、若函数 $f (x)$ 在区间 $[0, π]$ 上恰有一个零点，则ω的范围为 $[\frac{1}{4}, \frac{5}{4})$

查看试题解析
11. 已知函数 $f (x) = x^{4} - \log_{b} x$ ，则下列关于 $f (x)$ 说法正确的是（）

A、当 $b \in (0, 1), f (x)$ 有且只有一个零点，设其为 $x_{0}$ ，则 $x_{0} > b$ B、当 $b > 2$ 时，关于x的不等式 $f (x) < 0$ 有解 C、当 $b = e$ 时，若 $x_{1}, x_{2}$ 满足 $f (x_{1}) = f (x_{2})$ ，则 $x_{1}^{4} + x_{2}^{4} > \frac{1}{2}$ D、 $f (x) = 0$ 有两解的充要条件是 $b \in (1, e^{\frac{1}{4 e}})$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分．

12. 若曲线 $y = e^{x} + x$ 与曲线 $y = x^{3} + a x + 1$ 在点 $(0, 1)$ 处有相同的切线，则 $a =$ ．

查看试题解析
13. 已知 $α \in (0, π), \cos (α + \frac{π}{6}) = \frac{\sqrt{10}}{10}$ ，则 $\cos (2 α - \frac{π}{6}) =$ ．

查看试题解析
14. 已知数列 $\{a_{n}\}$ 满足 $a_{n + 1} = {(- 1)}^{n} a_{n} + n (n \in N^{*}), a_{2025} = 2025$ ，则 $a_{1} =$ ．

查看试题解析

四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．

15. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ，点P为 $△ A B C$ 内部一点， $A C = 4 \sqrt{2}, C P = 5, B P = 3$ ．

(1)、若 $A P = 3$ ，求 $△ A B P$ 的面积；

(2)、若 $\sin ∠ A B P = \frac{\sqrt{2}}{6}$ ，求 $A P$ 的长．

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A D = \sqrt{2}$ ，取 $C D$ 中点 $M$ ，将 $△ A D M$ 和 $△ B C M$ 分别沿直线 $A M$ ， $B M$ 折叠，使 $D$ ， $C$ 两点重合于点 $P$ 得到三棱锥 $P - A B M$ ．

(1)、当 $A B = 2$ 时，求证： $A M ⊥ P B$ ；

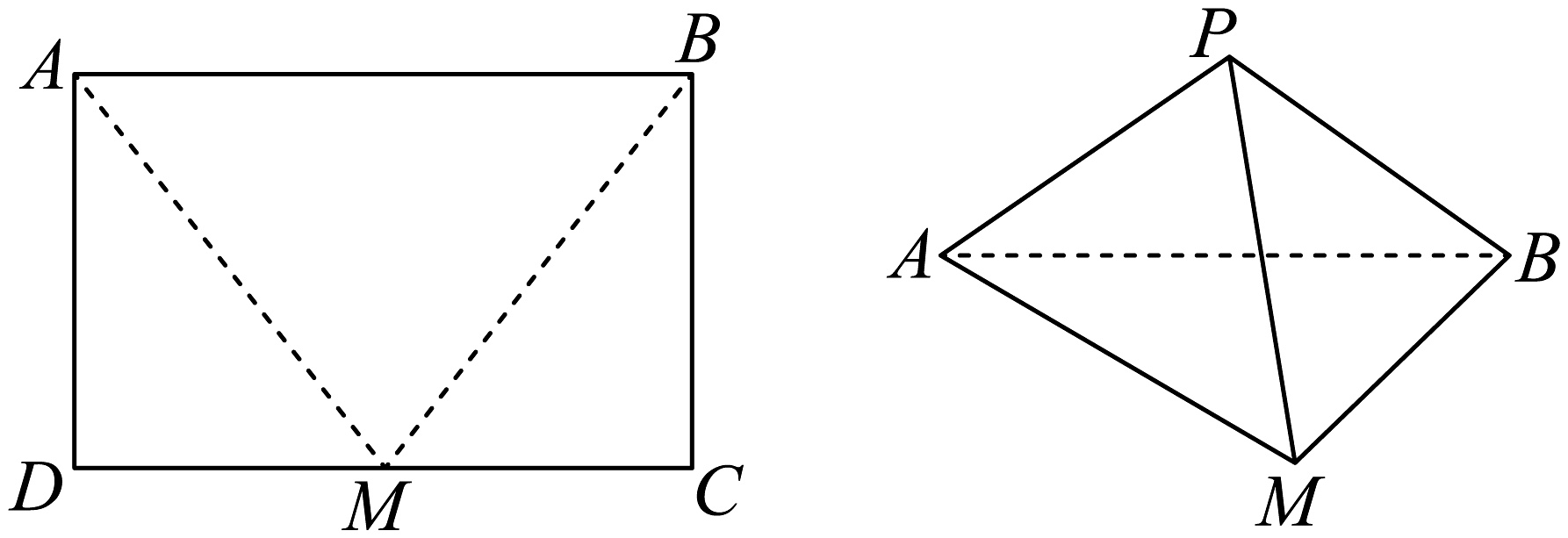(2)、若二面角 $A - P M - B$ 的平面角为 $60^{\circ}$ ，是否存在 $A M$ 上一点 $E$ ，使得 $P E$ 与平面 $P B M$ 所成角的正弦值为 $\frac{\sqrt{15}}{5}$ ？若存在，请求出 $E$ 点的位置；若不存在，请说明理由．

查看试题解析
17. 用红、黄、蓝、绿、紫五种不同颜色中的若干种给正四棱锥 $P - A B C D$ 的五个顶点着色，要求相邻两个顶点的颜色不同．

(1)、记“给顶点A、C涂不同的颜色”为事件M，“完成全部顶点的着色用了4种不同的颜色”为事件N，求 $P (M | N)$ ．

(2)、设完成全部顶点的着色所用的颜色种数为X，求X的概率分布列及数学期望．

查看试题解析
18. 已知平面内一动圆过点 $(0, 1)$ ，且该圆被x轴截得的弦长为2，设其圆心的轨迹为曲线E．

(1)、求曲线E的方程；

(2)、点A为曲线E上一点（不同于原点），过点A作E的切线l，经过点A并且垂直于l的直线与E相交于点B，点C为E上一点并且满足 $B C ∥ l$ ．
（ⅰ）若点A的坐标为 $(2, 2)$ ，求直线 $B C$ 的方程；
（ⅱ）求 $△ A B C$ 面积的最小值．

查看试题解析
19. 曼哈顿距离是人工智能中常用的一种测距方式，其定义为：设 $A (x_{1}, y_{1}), B (x_{2}, y_{2})$ ，则A，B之间的曼哈顿距离为 $d (A, B) = |x_{1} - x_{2}| + |y_{1} - y_{2}|$ ．现已知直线 $l : 2 x - 2 y + 5 = 0$ ，点P是直线l上一动点．

(1)、若点 $Q (2, 5)$ ，试计算 $d (P, Q)$ 的取值范围；

(2)、若点 $A_{1} (1, 6), A_{2} (2, 5), A_{3} (3, 4)$ ，试计算 $d (P, A_{1}) + d (P, A_{2}) + d (P, A_{3})$ 的最小值；

(3)、若点M是函数 $y = \ln x$ 图象上一动点，求 $d (P, M)$ 的最小值，并求当 $d (P, M)$ 取最小值时对应的点P的轨迹的长度．

查看试题解析