浙教版（2024) 数学八年级上册第2章特殊三角形单元检测基础卷

试卷更新日期：2025-08-27 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 2024年巴黎奥运会中国体育代表团取得了40金27银24铜的优异成绩，下列巴黎运动会体育图标是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在下列条件中：① $∠ A + ∠ B = ∠ C$ ， ② $∠ A : ∠ B : ∠ C = 1 : 5 : 6$ ， ③ $∠ A = 90 ° - ∠ B$ 中，能确定 $△ A B C$ 是直角三角形的条件有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 如图， $A D$ 是等腰 $△ A B C$ 底边 $B C$ 上的中线，点 $E$ 在 $A D$ 上，且 $B E ⊥ C E$ ，若 $∠ B A C = 70 °$ ，则 $∠ A B E$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $20 °$ D、 $25 °$

查看试题解析
4. 如图， $B E = C F$ ， $A E ⊥ B C$ ， $D F ⊥ B C$ ，要根据“ $H L$ ”证明 $R t △ A B E$ ≌ $R t △ D C F$ ，则还要添加一个条件是（）

A、 $∠ A = ∠ D$ B、 $∠ B = ∠ C$ C、 $A E = B F$ D、 $A B = D C$

查看试题解析
5. 如图，点 $A, B, C$ 和点 $D_{1}, D_{2}, D_{3}, D_{4}, D_{5}$ 都在正方形网格的格点上，则能与点 $A, B, C$ 组成轴对称图形的 $D$ 点的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B D$ 平分 $∠ A B C$ ，若 $∠ A = 40 °$ ，则 $∠ D B C$ 的度数为（）

A、 $30 °$ B、 $35 °$ C、 $40 °$ D、 $45 °$

查看试题解析
7. “等腰三角形的两个底角相等”的逆命题是（）

A、在同一个三角形中，等边对等角 B、两个角互余的三角形是等腰三角形 C、如果一个三角形有两个角相等，那么这个三角形是等腰三角形 D、如果一个三角形有两条边相等，那么这个三角形是等腰三角形

查看试题解析
8. 如图，已知射线OM，以O为圆心，任意长为半径作弧，与射线OM交于点A，再以点A为圆心，AO长为半径作弧，两弧交于点B，作射线OB，那么∠AOB的度数是( ).

A、90° B、60° C、45° D、30°

查看试题解析
9. 如图，已知 $△ A B C$ 的面积为28， $A B = A C = 16$ ，点 $D$ 为 $B C$ 边上一点，过点 $D$ 分别作 $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ，若 $D F = 2 D E$ ，则 $D F$ 长为（）

A、 $\frac{7}{3}$ B、 $\frac{7}{6}$ C、 $\frac{16}{3}$ D、6

查看试题解析
10. 若实数 $m$ ， $n$ 满足等式 $|m - 2| + \sqrt{n - 4} = 0$ ，且 $m$ ， $n$ 恰好是等腰三角形 $A B C$ 的两条边的长，则 $△ A B C$ 的周长是（）

A、8 B、10 C、8或10 D、6

查看试题解析

二、填空题（每题3分，共18分）

11. 命题“等边三角形有一个角是 $60^{\circ}$ ”的逆命题是．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 8$ ， $B C = 6$ ， $B D$ 为 $△ A B C$ 的角平分线，则 $△ A B D$ 的面积为．

查看试题解析
13. 如图， $D$ 为 $R t △ A B C$ 中斜边 $B C$ 上的一点，且 $B D = A B$ ，过点 $D$ 作 $B C$ 的垂线，交 $A C$ 于点 $E$ ，若 $A E = 6 c m$ ， $D C = 8 c m$ ，则 $C E =$ $c m$ .

查看试题解析
14. 等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分，则这个等腰三角形底边的长为cm.

查看试题解析
15. 如图，有两棵树，一棵高10m，另一棵高4m，两树相距8m．一只小鸟从一棵树的树尖飞到另一棵树的树尖，那么这只小鸟至少要飞行m．

查看试题解析
16. 如图，在长方形 $A B C D$ 中，点E是边 $B C$ 上一点，将 $△ D C E$ 沿 $D E$ 折叠，使得点C落在 $A B$ 上，连结 $D C^{'}$ 、 $E C^{'}$ ，点F是 $D C^{'}$ 的中点，连结 $C F$ ， $B C = \sqrt{7}$ ，且 $3 ∠ A C^{'} D = 2 ∠ B C F$ ，则 $C D$ 的长为．

查看试题解析

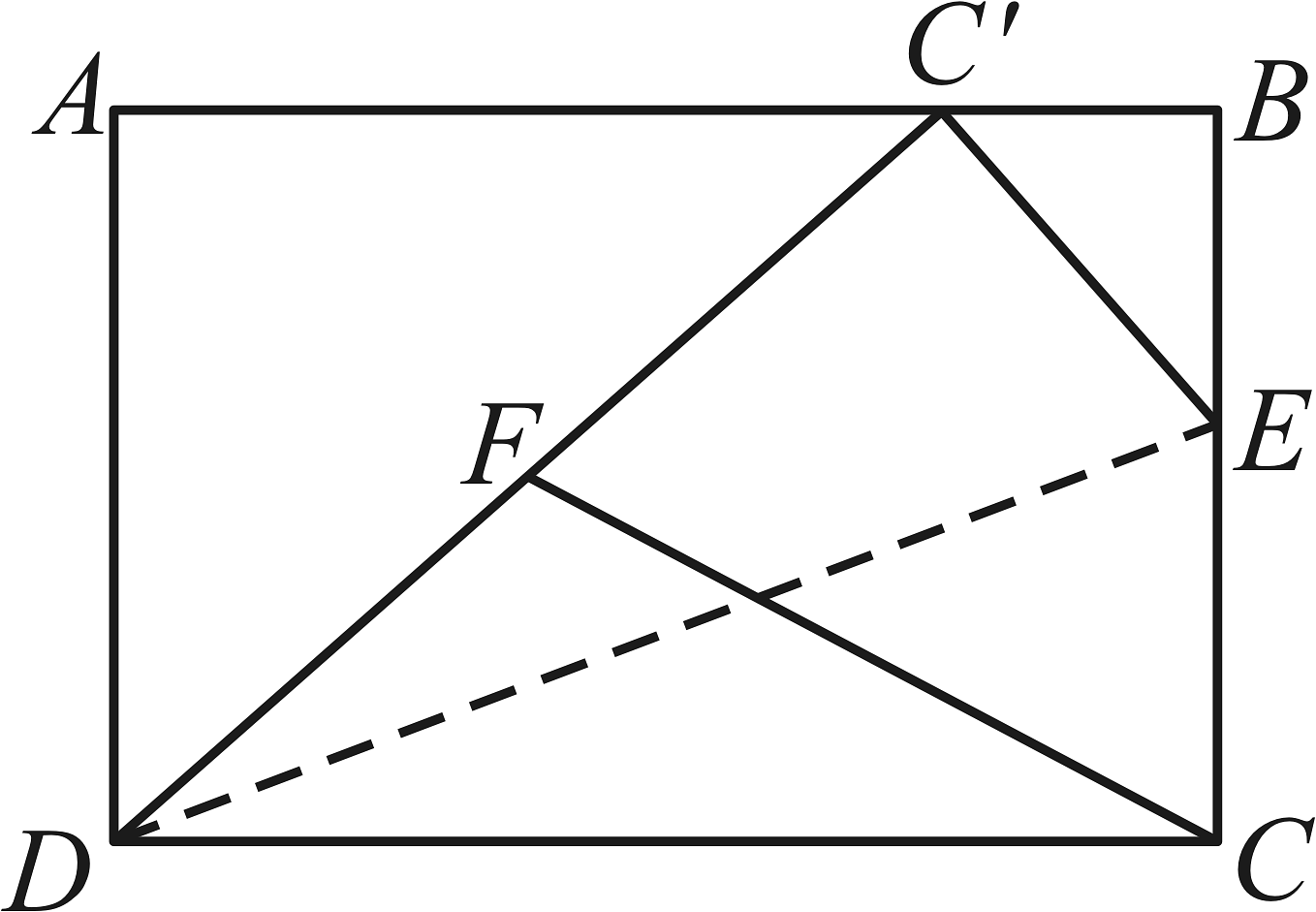
三、解答题（共8题，共72分）

17. 五根小木棒的长度分别是7cm， 15cm， 20cm，24cm，25cm，现将它们摆成两个直角三角形，如图所示的三个图形中哪个是正确的?

查看试题解析
18. 尺规作图：以线段a，b(如图)为边作等腰三角形ABC.

查看试题解析
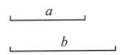19. 如图，在四边形ABCD中，AB∥CD，E为BC上一点，且∠BAE=25°，∠CDE=65°．求证：△ADE是直角三角形.

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D，E分别在 $B A ， C B$ 的延长线上，且 $A E = C D$ ， $∠ B A E = ∠ A C D$ ．求证： $△ A B C$ 是等边三角形．

查看试题解析
21. 已知：如图， $A C$ ， $B D$ 交于点 $O$ ， $∠ A = ∠ D = 90 °$ ， $A C = B D$ ．求证： $O B = O C$ ．

查看试题解析
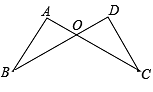22. 如图1，在△ABC中，AB=AC，P为底边BC上一点，PE⊥AB，PF⊥AC，CH⊥AB，垂足分别为E，F，H．易证PE+PF=CH．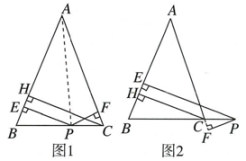
证明过程如下：
如图1，连结AP．
∵PE⊥AB，PF⊥AC，CH⊥AB，
∴S_△_ABP= $\frac{1}{2}$ AB·PE，S_△_ACP= $\frac{1}{2}$ AC·PF，S_△_AB_C= $\frac{1}{2}$ AB·CH．
又∵S_△_ABP+S_△_ACP=S_△_ABC ，
∴AB·PE+AC·PF=AB·CH．
∵AB=AC，
∴PE+PF=CH．
如图2，当P为BC延长线上的点时，其他条件不变，PE，PF，CH又有怎样的数量关系？请写出你的猜想，并加以证明．

查看试题解析
23. 综合与实践
如图，在 $△ A B C$ 中， $∠ A B C = 9 0^{°}$ .以点 $A$ 为圆心，AB为半径画弧，交AC于点 $D$ ，连接BD.过点 $D$ 作BD的垂线，交BC于点 $E$ .
观察这个图形，同学们纷纷提出自己的想法.

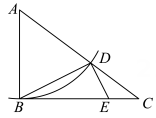(1)、圆圆说：“ $∠ D B E = ∠ C D E$ .”你认为圆圆的说法正确吗？请说明理由.

(2)、方方说：“若 $B D = 2 D E$ ，则 $B E = A D$ .”请你证明结论.

(3)、小明说：“给出条件 $B E = 2 C D$ ，就可以确定 $∠ A$ 的度数.”请你直接写出 $∠ A$ 的度数.

查看试题解析

24.

项目背景	我校八年级兴趣小组对“勾股树”展开了研究．
素材一	毕达哥拉斯树，也叫“勾股树”．是由毕达哥拉斯根据勾股定理画出来的一个可以无限重复的树形图形，因为重复数次后的形状好似一棵树，被称为毕达哥拉斯树．
素材二	经过小组讨论，制定了如下规则： 1．画出不同类型三角形形成的树形图； 2．所画的基础三角形周长均为 $7 cm$ ，其中一条边长固定为 $2 cm$ ，根据规则，三位同学分别画出了不同类型的树形图并进行探究．
素材三
解决问题
任务一	小明画出了锐角 $△ A B C ， A B = A C ， B C = 2 cm$ ，则 $S_{2} =$ 　　　 ${cm}^{2}$ ．
任务二	小金画出了直角 $△ D E F ， ∠ D F E = 90 ° ， E F = 2 cm$ ，计算 $S_{2}$ 的值，并写出过程．
任务三	小山画出了钝角 $△ G H I ， ∠ G I H = 120 ° ， H I = 2 cm$ ，则 $S_{2} {=_____cm}^{2}$ ．

查看试题解析

浙教版（2024) 数学八年级上册第2章 特殊三角形 单元检测基础卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

浙教版（2024) 数学八年级上册第2章特殊三角形单元检测基础卷