浙教版（2024) 数学八年级上册2.8 直角三角形全等的判定 同步分层练习

试卷更新日期：2025-08-27 类型：同步测试

进入 出卷网 下载

一、夯实基础：

  • 1. 如图，BE=CF ， AE⊥BC ， DF⊥BC ， 要根据“HL”证明Rt△ABE≌Rt△DCF ， 则还要添加一个条件是（ ）

    A、∠A=∠D B、∠B=∠C C、AE=BF D、AB=DC

    查看试题解析

  • 2. 如图，最适合用“HL”定理判定Rt△ABC和Rt△DEF全等的条件是（ ）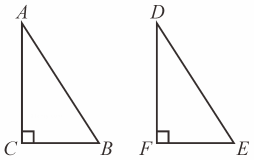

    A、AC=DF，BC=EF． B、∠A=∠D，AB=DE． C、AC=DF，AB=DE． D、∠B=∠E，BC= EF．

    查看试题解析

  • 3. 如图，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．下列结论中，不正确的是（    ）

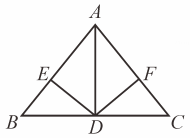    A、DA平分∠EDF B、AE=AF C、AD上任一点P到AB，AC的距离相等 D、AB，AC上的点到AD的距离相等

    查看试题解析

  • 4. 如图，在△ABC中，∠C=90° ， DE⊥AB于点D ， BC=BD.如果AC=4 cm ， 那么AE+DE=（ ）

    A、2cm B、4cm C、3cm D、5cm

    查看试题解析

  • 5. 如图，OC是∠AOB内部的一条射线，P是射线OC上任意一点，PD⊥OA ， PE⊥OB.下列条件：①∠AOC=∠BOC；②PD=PE；③OD=OE；④∠DPO=∠EPO ， 其中，能判定OC是∠AOB的平分线的有（      ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 6. 如图，AC⊥BC，AD⊥BD，垂足分别是C，D.若要根据“HL”得到Rt△ABC≌Rt△BAD，则应添加的条件是.(写一种即可)

    查看试题解析

  • 7. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图，一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P ， 小明说：“射线OP就是∠BOA的平分线.”小明的做法，其理论依据是.

    查看试题解析

  • 8. 下列命题中逆命题是真命题的是.（写序号）

    （ 1 ）直角三角形两条直角边的平方和等于斜边的平方；

    （ 2 ）等腰三角形两腰上的高线相等；

    （ 3 ）若三条线段 a ， b ， c 是三角形的三边，则这三条线段满足 a+b>c ；

    （ 4 ）角的内部，到角两边距离相等的点在这个角的平分线上.

    （ 5 ）全等三角形的面积相等.

    查看试题解析

  • 9. 如图， 已知 FE⊥AD,CB⊥AD,AE=DB,AC=DF ，  点 A， E， B， D 在同一直线上， A C 与 F D 相交于点 G ，  求证： GA=GD. 请补全证明过程， 并在括号里写上理由.

    证明： ∵FE⊥AD,CB⊥AD ，

    ∴∠FED=    ▲        =90°

    ∵AE=DB，

    ∵AE+    ▲        =    ▲        +BD，

    即AB=DE.

    在Rt△ABC与Rt△DEF中，

    {AB=DEAC=DF’

    ∴Rt△ABC≌Rt△DEF（    ▲        ）

    ∴∠A=    ▲

    ∴GA=GD（    ▲        ）

    查看试题解析

二、能力提升：

  • 10. 用三角尺可按下面方法画角平分线： 在已知的∠AOB的两边上，分别截取OM=ON ， 再分别过点M、N作OA、OB的垂线，交点为P ， 画射线OP ， 则OP平分∠AOB ． 这样画图的主要依据是（     ）

    A、SAS B、ASA C、AAS D、HL

    查看试题解析

  • 11. 如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于12MN长为半径画弧，两弧交点O，作射线AO，交BC于点E.已知CE＝3，BE＝5，则AC的长为（　　）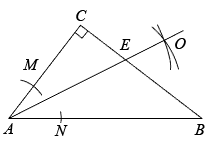

    A、8 B、7 C、6 D、5

    查看试题解析

  • 12. 如图，在△ABC中，BE ， CD分别平分∠ABC和∠ACB ， BE ， CD相交于点P，则下列结论不一定成立的是（     ）

    A、∠BAP=∠CAP B、△ABP与△ACP的面积比等于边AB与AC之比 C、BC=AP+AC D、若∠BAC=60° ， 则∠BPC=120°

    查看试题解析

  • 13. 如图所示，P，Q分别是BC，AC上的点，作PR⊥AB于点R ， 作PS⊥AC于点S ， 若AQ=PQ ， PR=PS ， 下面三个结论：①AS=AR；②QP//AR；③△BRP≅△CSP ， 其中，正确的是.(填序号)

    查看试题解析

  • 14. 如图，AD是△ABC的角平分线，DF⊥AB ， 垂足为F，DE=DG ， △ADG和△AED的面积分别为27和14，则△EDF的面积为 ．

    查看试题解析

  • 15. 如图，在Rt△ABC中，∠ACB＝90°，两直角边AC＝8cm ， BC＝6cm ．

    (1)、作∠BAC的平分线AD交BC于点D；（尺规作图，不写作法，保留作图痕迹）
    (2)、计算△ABD的面积．

    查看试题解析

  • 16. 如图，在△ABC中， ∠C=90°，BD平分∠ABC交AC于点D，过点D作DE⊥AB于点E，点F，在BC上，使DF=AD.

    (1)、求证：Rt△ADE≌Rt△FDC.
    (2)、请判断CF，AB，BF之间的数量关系，并说明理由.

    查看试题解析

三、拓展创新：

  • 17. 学习了三角形全等的判定与性质后，我们得到角平分线的性质定理及其逆定理.

    (1)、【理解定理】如图1，已知AD平分∠CAB，DC⊥AC于C，DB⊥AB于B，若CD=1，则DB=.
    (2)、【问题解决】如图2，点B，D，C分别是AF，AG和AE上的一点，且满足BD=CD，∠ABD+∠ACD=180°.

    求证：AD平分∠BAC.

    (3)、【变式应用】如图3，在△ABC中，AB=AC=5，BC=6，D为BC的中点，E，F分别为AB，AC上一点，且∠BED=∠AFD.

    求△BDE和△CDF的面积和.

    查看试题解析