浙教版(2024) 数学八年级上册2.7.2 探索勾股定理 同步分层练习
试卷更新日期:2025-08-27 类型:同步测试
一、夯实基础:
-
1. 将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )A、2、3、4 B、4、5、6 C、5、11、12 D、8、15、172. 在下列条件中,不能判断是直角三角形的是( )A、 , B、 , , C、 , D、 ,3. 如果的三边分别为 , 其中为大于1的正整数,则( )A、是直角三角形,且斜边为 B、是直角三角形,且斜边为2m C、是直角三角形,且斜边为 D、不是直角三角形4. 如图,正方形ABCD是由9个边长为1的小正方形组成的,每个小正方形的顶点都叫格点,连结AE,AF,则∠EAF的度数为( )
 A、30° B、45° C、60° D、35°5. 如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形,那么这四个三角形中,不是直角三角形的是( )A、
A、30° B、45° C、60° D、35°5. 如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形,那么这四个三角形中,不是直角三角形的是( )A、 B、
B、 C、
C、 D、
D、 6. 三角形的三边长分别为a、b、c,且满足 , 则这个三角形是( )A、等边三角形 B、钝角三角形 C、直角三角形 D、锐角三角形7. 若三角形的三边之比为 , 则此三角形为三角形.8. 如果三角形中两边的平方和等于第三边的平方,那么这个三角形是 , 最大边所对的角是.9. 如图,在△ABC中,已知∠A为钝角,边AB,AC的中垂线分别交BC于点D,E.若BD2+CE2=DE2 , 则∠A= .
6. 三角形的三边长分别为a、b、c,且满足 , 则这个三角形是( )A、等边三角形 B、钝角三角形 C、直角三角形 D、锐角三角形7. 若三角形的三边之比为 , 则此三角形为三角形.8. 如果三角形中两边的平方和等于第三边的平方,那么这个三角形是 , 最大边所对的角是.9. 如图,在△ABC中,已知∠A为钝角,边AB,AC的中垂线分别交BC于点D,E.若BD2+CE2=DE2 , 则∠A= .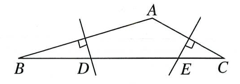 10. 如图,在四边形中, , , , , . 求四边形的面积.
10. 如图,在四边形中, , , , , . 求四边形的面积.
二、能力提升:
-
11. 下列条件中,不能判定是直角三角形的是( )A、 B、 C、 D、12. 勾股定理最早出现在《周髀算经》:“勾广三,股修四,弦隅五”,观察下列勾股数:3,4,5;5,12,13;7,24,25;这类勾股数的特点如下:勾为奇数,弦与股相差1,柏拉图研究了勾为偶数,弦与股相差2的一类勾股数,如:6,8,10;8,15,17;若此类勾股数的勾为( , 为正整数),则弦是(结果用含的式子表示)( )A、 B、 C、 D、13. 在中,∠A,∠B,∠C的对边分别是a,b,c,且满足(则是三角形.14. 如图,已知CD=3,AD=4,BC=12,AB=13,∠ADC=90°,则阴影部分的面积为.
 15. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 .
15. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 . 16. 台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向 由 行驶向 ,已知点 为一海港,且点 与直线 上的两点 , 的距离分别为 , ,又 ,以台风中心为圆心周围 以内为受影响区域.
16. 台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向 由 行驶向 ,已知点 为一海港,且点 与直线 上的两点 , 的距离分别为 , ,又 ,以台风中心为圆心周围 以内为受影响区域.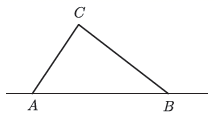 (1)、求 的度数.(2)、海港 受台风影响吗?为什么?(3)、若台风的速度为20千米/小时,当台风运动到点 处时,海港 刚好受到影响,当台风运动到点 时,海港 刚好不受影响,即 ,则台风影响该海港持续的时间有多长?17. 如图1,ΔABC和ΔCDE都是等腰直角三角形,∠ACB=∠DCE=90°,D为ΔABC外一点,AB>2CD,A,C,E三点不共线,连结AD,AE,BD,BE,AE与BD交于点F
(1)、求 的度数.(2)、海港 受台风影响吗?为什么?(3)、若台风的速度为20千米/小时,当台风运动到点 处时,海港 刚好受到影响,当台风运动到点 时,海港 刚好不受影响,即 ,则台风影响该海港持续的时间有多长?17. 如图1,ΔABC和ΔCDE都是等腰直角三角形,∠ACB=∠DCE=90°,D为ΔABC外一点,AB>2CD,A,C,E三点不共线,连结AD,AE,BD,BE,AE与BD交于点F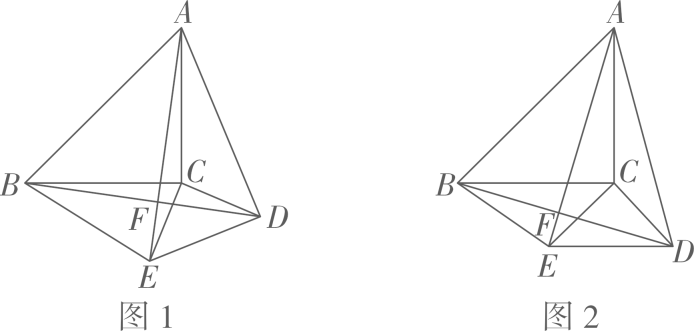 (1)、求证:AE=BD;(2)、当AD2+2CD2=BD2时,求∠ADC的度数;(3)、如图2,当BC∥DE时,CD= , AC=3,求四边形△BED的面积.
(1)、求证:AE=BD;(2)、当AD2+2CD2=BD2时,求∠ADC的度数;(3)、如图2,当BC∥DE时,CD= , AC=3,求四边形△BED的面积.三、拓展创新:
-
18. 定义:如图,点M,N把线段AB分割成AM,MN,NB三条线段.若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
 (1)、已知点M,N把线段AB分割成AM,MN,NB三条线段.若AM=2,MN=4,则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边.若AB=12,AM=5,求BN的长.19. 为了测量如图墙体是否与地面垂直,即是否垂直于点 , 在没有角尺、量角器、刻度尺,只有足够长、足够多的若干条无弹性的绳子的情况下,三个数学兴趣小组分别设计了三种不同解决方案,其中第一、第二组的设计方案如下表.
(1)、已知点M,N把线段AB分割成AM,MN,NB三条线段.若AM=2,MN=4,则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边.若AB=12,AM=5,求BN的长.19. 为了测量如图墙体是否与地面垂直,即是否垂直于点 , 在没有角尺、量角器、刻度尺,只有足够长、足够多的若干条无弹性的绳子的情况下,三个数学兴趣小组分别设计了三种不同解决方案,其中第一、第二组的设计方案如下表.
问题
如何测量墙体是否与地面垂直?
工具
若干条无弹性的绳子
小组
第一小组
第二小组
第三小组
测量方案
模仿古埃及人用结绳的方法,在一条绳子上打个结,得到条线段,且用叠合法使得这条线段都相等,设每一条线段长为 . 如下图放置这总长是的绳子,使在上的绳子 , 在上的绳子 , 若 , 则 , 即于点 , 否则不垂直.
如图2,在射线 , 上分别取点 , , 放置绳子 , 对折得到相等的两段 , , 放置绳子 , 用叠合法比较与的长度,若 , 则墙体与地面垂直,即于点 , 否则不垂直.
测量示意图


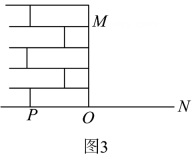 (1)、第一、二小组的方案可行吗?如果可行,请分别给出证明;如果不可行,请说明理由.(2)、请你代表第三小组,写出一个方案的应用原理不同于上述第一、第二小组的测量方案,并画出测量示意图,然后证明方案的可行性.
(1)、第一、二小组的方案可行吗?如果可行,请分别给出证明;如果不可行,请说明理由.(2)、请你代表第三小组,写出一个方案的应用原理不同于上述第一、第二小组的测量方案,并画出测量示意图,然后证明方案的可行性.