浙教版(2024) 数学八年级上册2.7.1 探索勾股定理 同步分层练习
试卷更新日期:2025-08-26 类型:同步测试
一、夯实基础:
-
1. 如图,在Rt中, , 边BC的长是( )
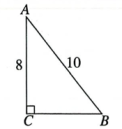 A、5 B、6 C、8 D、2. 在中,若 , 则( )A、 B、 C、 D、3. 如图,在中, , , 点A恰好落在数轴上表示的点上,以原点O为圆心,的长为半径画弧交数轴于点P,使点P落在点A的左侧,则点P所表示的数是( )
A、5 B、6 C、8 D、2. 在中,若 , 则( )A、 B、 C、 D、3. 如图,在中, , , 点A恰好落在数轴上表示的点上,以原点O为圆心,的长为半径画弧交数轴于点P,使点P落在点A的左侧,则点P所表示的数是( )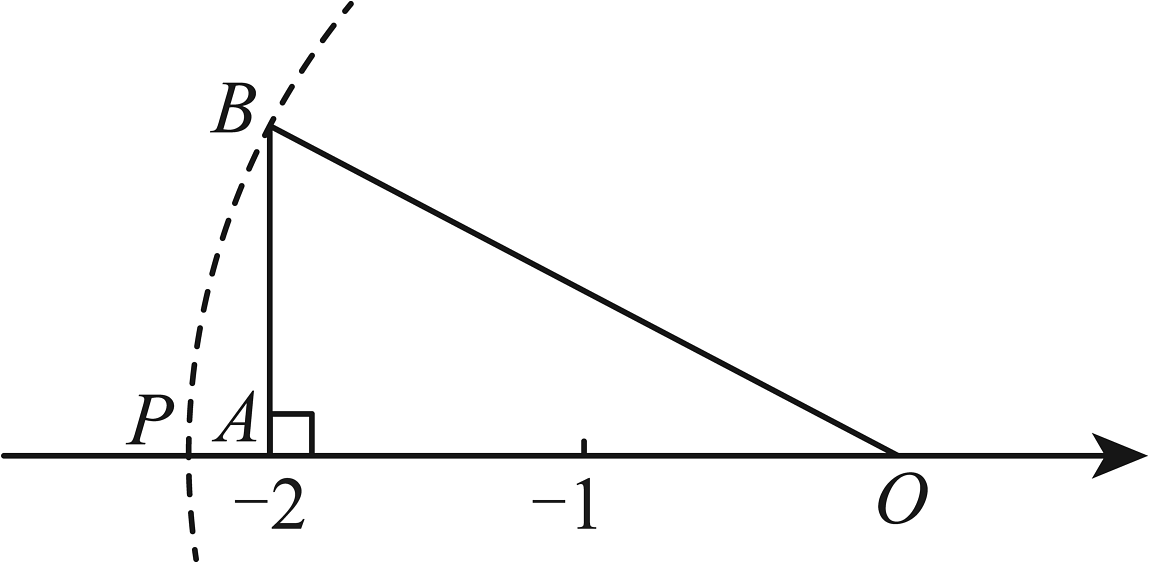 A、 B、 C、 D、4. 如图,三条直线互相平行,的三个顶点分别在三条平行线上.已知 , , 且之间的距离为2,之间的距离为3,则的面积为( )
A、 B、 C、 D、4. 如图,三条直线互相平行,的三个顶点分别在三条平行线上.已知 , , 且之间的距离为2,之间的距离为3,则的面积为( ) A、6 B、 C、10 D、135. 直角三角形的三边为 且 都为正整数,则三角形其中一边长可能为 ( ).A、61 B、71 C、81 D、916. 若直角三角形的两边长分别是5和12,则它的斜边长是( )A、13 B、13或 C、 D、12或137. 直角三角形两条直角边的平方和等于 , 如果a,b为直角三角形的两条直角边的长,c为斜边的长,则.8. 如图,在△ABC中,AB=AC=5,BC=6,D是BC的中点,则AD的长是.
A、6 B、 C、10 D、135. 直角三角形的三边为 且 都为正整数,则三角形其中一边长可能为 ( ).A、61 B、71 C、81 D、916. 若直角三角形的两边长分别是5和12,则它的斜边长是( )A、13 B、13或 C、 D、12或137. 直角三角形两条直角边的平方和等于 , 如果a,b为直角三角形的两条直角边的长,c为斜边的长,则.8. 如图,在△ABC中,AB=AC=5,BC=6,D是BC的中点,则AD的长是. 9. 已知直角三角形的两边长分别为5和12,则斜边上的中线长为.10. 如图,在中,.求:
9. 已知直角三角形的两边长分别为5和12,则斜边上的中线长为.10. 如图,在中,.求: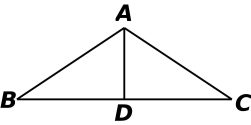 (1)、BC边上的中线AD的长(2)、求△ABC的面积.
(1)、BC边上的中线AD的长(2)、求△ABC的面积.二、能力提升:
-
11. 如图,在中, , 点在AB边上,连结CD,点是CD的中点,连结AE.若 , 则AE的长是( )
 A、2 B、 C、 D、12. 如图,在中, , 为的中点,于点 , 若 , , 则为( ).
A、2 B、 C、 D、12. 如图,在中, , 为的中点,于点 , 若 , , 则为( ). A、 B、 C、 D、13. 如图,在锐角中, , , 的平分线交于点 , 、分别是和上的动点,则的最小值是( )
A、 B、 C、 D、13. 如图,在锐角中, , , 的平分线交于点 , 、分别是和上的动点,则的最小值是( )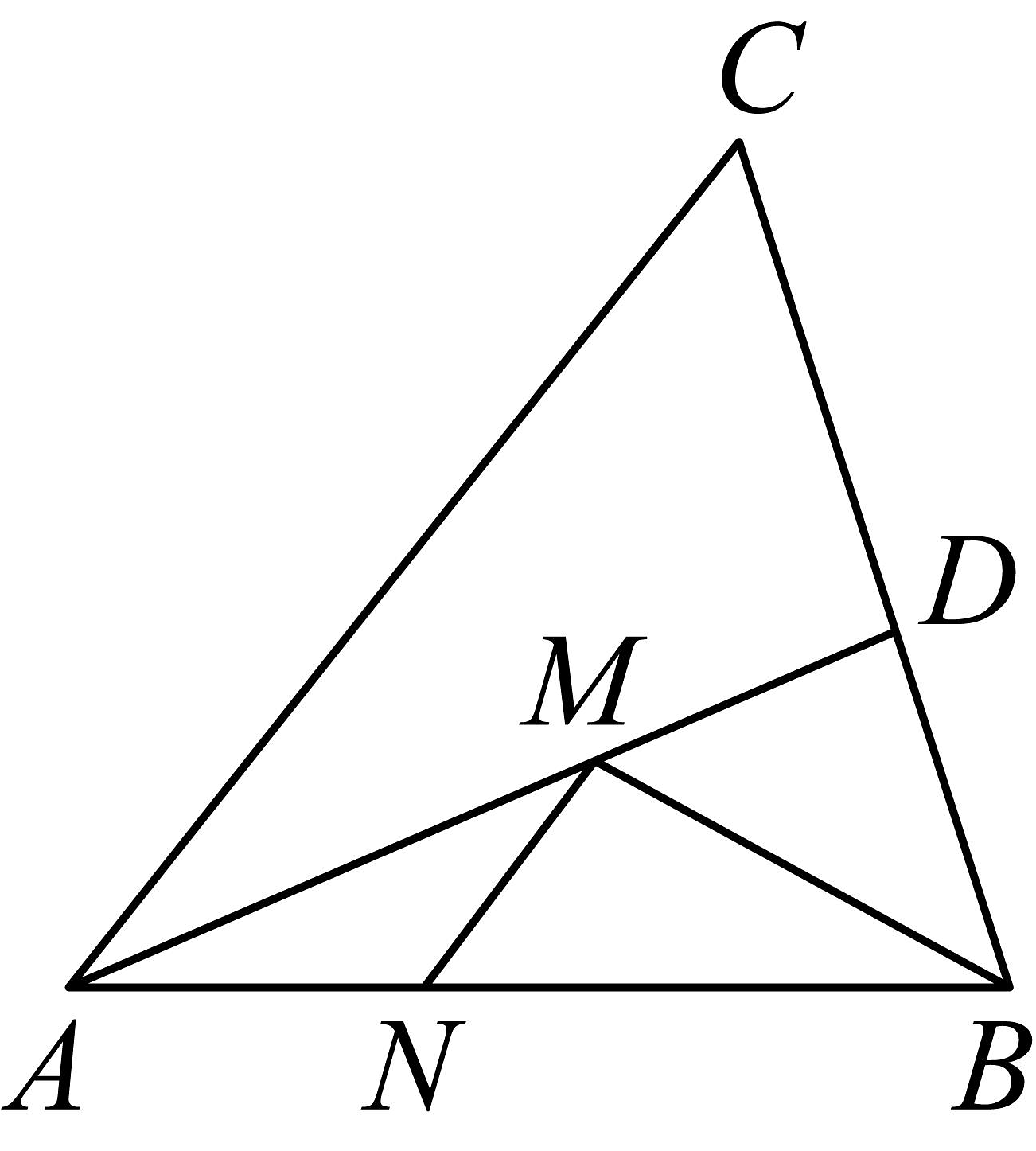 A、 B、 C、 D、14. 如图,在△ABC中,CB=90°,∠ACB=60°,点D,E分别为AB,AC上的动点,若BC=1,则CD+DE的最小值是.
A、 B、 C、 D、14. 如图,在△ABC中,CB=90°,∠ACB=60°,点D,E分别为AB,AC上的动点,若BC=1,则CD+DE的最小值是.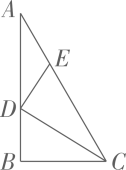 15. 如图,在 中, 于点 于点 ,并且点 是 的中点,的周长是 ,则 的长是。
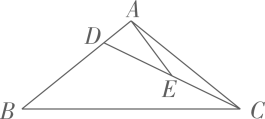
15. 如图,在 中, 于点 于点 ,并且点 是 的中点,的周长是 ,则 的长是。 16. 如图,AD是△ABC的高线,E为AB上一点,连结CE,交AD于点F,BE=CE.
16. 如图,AD是△ABC的高线,E为AB上一点,连结CE,交AD于点F,BE=CE. (1)、求证:△AEF是等腰三角形;(2)、若点F是CE的中点,CE=26,CD=12,求AF的长、17. 如图,在 中, 是 边上的高线, 是 边上的中线, ,点 是 中点.
(1)、求证:△AEF是等腰三角形;(2)、若点F是CE的中点,CE=26,CD=12,求AF的长、17. 如图,在 中, 是 边上的高线, 是 边上的中线, ,点 是 中点. (1)、求证: ;(2)、若 ,求 的长.
(1)、求证: ;(2)、若 ,求 的长.三、拓展创新:
-
18. 勾股定理是证明方法最多的定理之一,小明便以此建立项目,加以探究.

【问题提出】小明在做作业本时发现利用右图可以证明勾股定理.思路为利用面积法,将梯形的面积用不同的方式表示列出等式.由此猜想如果将Rt△DAF向左平移,能否证明勾股定理?
【方案设计】考虑到探究的难度,他首先设计了两种特殊的位置,开展研究:
方案
方案一
方案二
图形


备注
Rt△BCA≌Rt△EAD
Rt△BCA≌Rt△CFD
BC=a , AC=b , AB=c
【探究验证】首先验证方案一为方案二提供经验基础.
方式
验证过程
(分别用含有a , b , c的代数式完成填空)
图形
方式①
S四边形ADBE=S△ABE +S△ABD
S△ABE = ▲ . (以AE为底,高为BC)
S△ABD = ▲ . (以AD为底,则AD边上的高与AC等长)
连结BE , BD,不难得出AB⊥ED

方式②
S四边形ADBE =S△EBD +S△EAD
▲
综上所述利用方式①,②列出等式即可证明勾股定理.
【方法应用】
根据上述经验,请你继续完成方案二后续的证明过程.
提示:如图,连结BD , AD , 不难得出CD⊥BA , 利用两种方法表示四边形BCAD的面积.
