浙教版(2024) 数学八年级上册2.6.2 直角三角形 同步分层练习
试卷更新日期:2025-08-26 类型:同步测试
一、夯实基础:
-
1. 给定下列条件,不能判定三角形是直角三角形的是( )A、 B、 C、 D、2. 在下列条件中:① , ② , ③中,能确定是直角三角形的条件有( )A、0个 B、1个 C、2个 D、3个3. 如图, , 过点作于点 . 若 , 则的度数为( )
 A、 B、 C、 D、4. 如图,在△ABC 中,∠ACB=90°,AC=AE,BC=BF,则∠ECF=( ).
A、 B、 C、 D、4. 如图,在△ABC 中,∠ACB=90°,AC=AE,BC=BF,则∠ECF=( ). A、60° B、45° C、30° D、不确定5. 如图,在△ABC中,点P在边BC上(不与点B,点C重合) ,下列说法正确说法正确的是( )
A、60° B、45° C、30° D、不确定5. 如图,在△ABC中,点P在边BC上(不与点B,点C重合) ,下列说法正确说法正确的是( )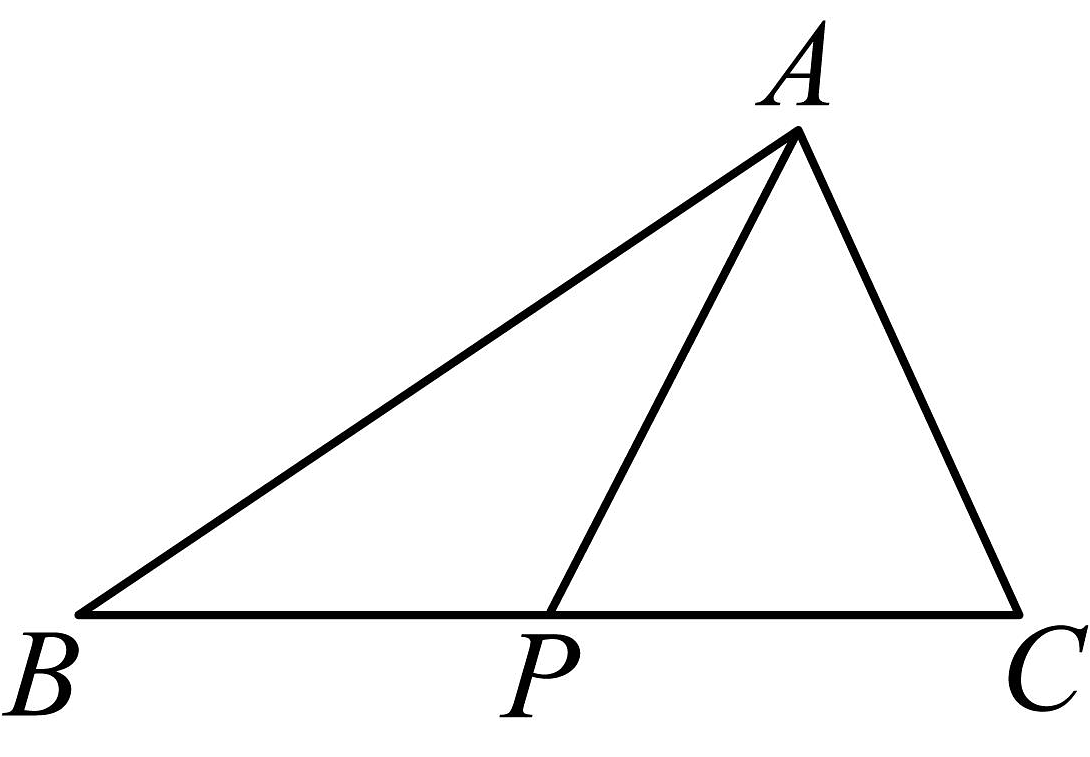 A、若∠BAC=90°,∠BAP=∠B,则AC=PC B、若∠BAC=90°,∠BAP=∠C,则AP⊥BC C、若AP⊥BC,PB=PC,则∠BAC=90° D、若PB=PC,∠BAP=∠CAP,则∠BAC=90°6. 如图,在中,点在边上,E,F分别是线段 , 的中点.若 , , 则( )
A、若∠BAC=90°,∠BAP=∠B,则AC=PC B、若∠BAC=90°,∠BAP=∠C,则AP⊥BC C、若AP⊥BC,PB=PC,则∠BAC=90° D、若PB=PC,∠BAP=∠CAP,则∠BAC=90°6. 如图,在中,点在边上,E,F分别是线段 , 的中点.若 , , 则( ) A、5 B、6 C、 D、47. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽像出的几何图形,B,C,E在同一条直线上,连结DC.
A、5 B、6 C、 D、47. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽像出的几何图形,B,C,E在同一条直线上,连结DC. (1)、请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的宇母);(2)、证明:DC⊥BE.
(1)、请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的宇母);(2)、证明:DC⊥BE.二、能力提升:
-
8. 如图,等腰中,腰上的高线为 , 的平分线为 , , 则为( )
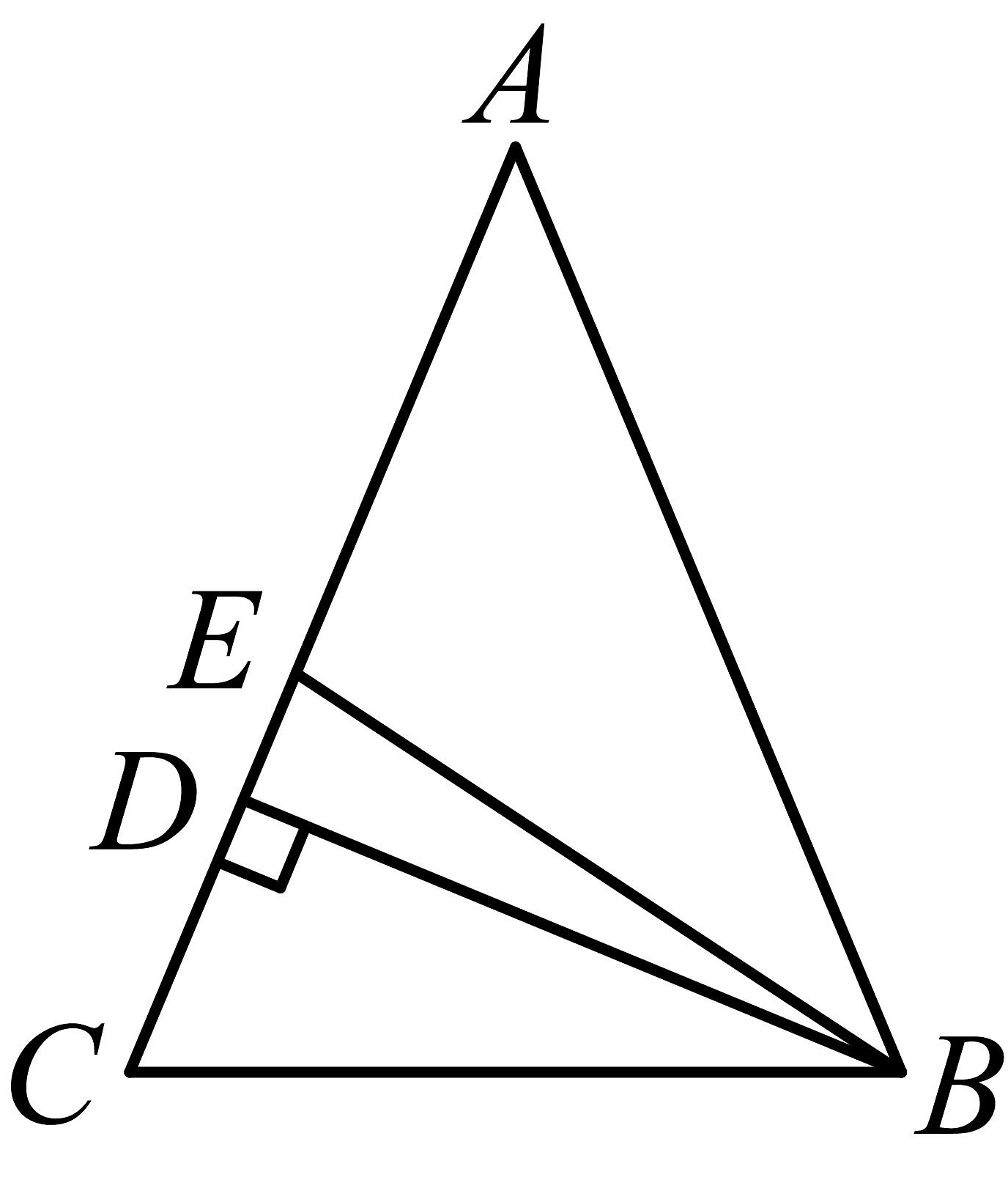 A、 B、 C、 D、9. 如图,在中, , 分别为边上的高线和的角平分线,于点F,当 , 时,的度数为( )
A、 B、 C、 D、9. 如图,在中, , 分别为边上的高线和的角平分线,于点F,当 , 时,的度数为( ) A、 B、 C、 D、10. 如图,在中,于点于点D,点F是的中点,连接设 , 则( )
A、 B、 C、 D、10. 如图,在中,于点于点D,点F是的中点,连接设 , 则( )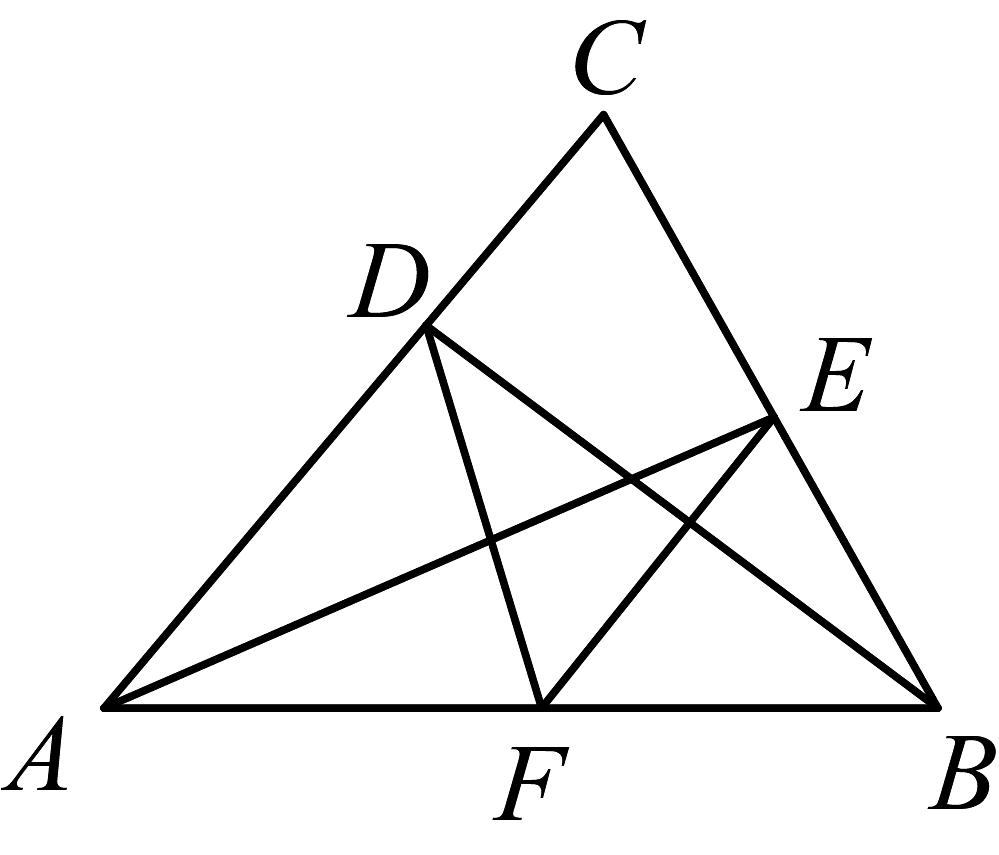 A、 B、 C、 D、11. 如图,在中, , 点是上一点,交延长线于点 , 连接交于点 , 已知 , 则下列结论:①;②;③;④ , 其中正确的结论有( )个.
A、 B、 C、 D、11. 如图,在中, , 点是上一点,交延长线于点 , 连接交于点 , 已知 , 则下列结论:①;②;③;④ , 其中正确的结论有( )个. A、1个 B、2个 C、3个 D、4个12. 如图,四边形中, , 平分 , , , 垂足为E,且 , 则的度数是 .
A、1个 B、2个 C、3个 D、4个12. 如图,四边形中, , 平分 , , , 垂足为E,且 , 则的度数是 . 13. 已知命题“如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形”,请按以下步骤完成此命题的证明.(1)、根据题意,画出图形:画及边上的中线 , 且满足;(画图工具不限)(2)、结合(1)中画出的图形,请写出已知与求证;(3)、证明:写出证明过程.
13. 已知命题“如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形”,请按以下步骤完成此命题的证明.(1)、根据题意,画出图形:画及边上的中线 , 且满足;(画图工具不限)(2)、结合(1)中画出的图形,请写出已知与求证;(3)、证明:写出证明过程.三、拓展创新:
-
14. 综合与实践
【问题情境】
数学课上老师组织同学们利用直角三角形纸片来进行拼图探究活动.
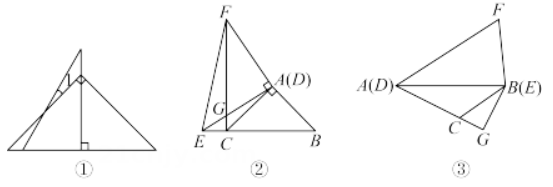 (1)、【实验探究】阳光小组将一张含30°角的直角三角形纸片和一张等腰直角三角形纸片按图①的方式摆放,则图中 .(2)、无敌小组将两张等腰直角三角形纸片和按图②的方式摆放,点A与点D以重合,且点B,C,E在同一直线上,连接CF交AE于点G,小组同学测量发现 , 请你帮他们证明此结论.(3)、【拓展探究】课后小强自制了两张三角形纸片和 , 其中 , , , 他把两张三角形纸片按图③的方式摆放(A与D重合,B与E重合).点C,F在AB两侧,过点B作 , 交AC的延长线于点G,小强发现线段AC,AF,CG之间存在一定的数量关系,请你探究此关系并加以证明.
(1)、【实验探究】阳光小组将一张含30°角的直角三角形纸片和一张等腰直角三角形纸片按图①的方式摆放,则图中 .(2)、无敌小组将两张等腰直角三角形纸片和按图②的方式摆放,点A与点D以重合,且点B,C,E在同一直线上,连接CF交AE于点G,小组同学测量发现 , 请你帮他们证明此结论.(3)、【拓展探究】课后小强自制了两张三角形纸片和 , 其中 , , , 他把两张三角形纸片按图③的方式摆放(A与D重合,B与E重合).点C,F在AB两侧,过点B作 , 交AC的延长线于点G,小强发现线段AC,AF,CG之间存在一定的数量关系,请你探究此关系并加以证明.