浙教版(2024) 数学八年级上册2.6.1 直角三角形 同步分层练习
试卷更新日期:2025-08-26 类型:同步测试
一、夯实基础:
-
1. 直角三角形的一个锐角为34°,则它的另一个锐角为( ).A、34° B、36° C、56° D、66°2. 中, ,则 的度数为( )A、50° B、60° C、70° D、80°3. 已知,在Rt中,为直角,是的2倍,则的度数是( )A、 B、 C、 D、4. 如图,在中, , 则( )
 A、 B、 C、 D、5. 如图,在Rt中,是斜边AB上的中线,若 , 则AB的长为( )
A、 B、 C、 D、5. 如图,在Rt中,是斜边AB上的中线,若 , 则AB的长为( ) A、2.5 B、4 C、5 D、66. 如图,一根竹竿AB斜靠在竖直的墙上,点P是AB的中点,A'B'表示竹竿AB上下滑动时的情形,则下列判断正确的是( )
A、2.5 B、4 C、5 D、66. 如图,一根竹竿AB斜靠在竖直的墙上,点P是AB的中点,A'B'表示竹竿AB上下滑动时的情形,则下列判断正确的是( )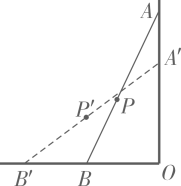 A、下滑时,OP的长度增大 B、上升时,OP的长度减小 C、只要滑动,OP的长度就变化 D、无论怎样滑动,OP的长度不变7. 在△ABC中, ∠C=90°,∠A=∠B,则B=8. 直角三角形ABC中,∠ACB=90°,点D是AB的中点,若AB=10,则CD的长为 .9. 如图,在△ABC中,AB=AC , ∠A=30°,BD是AC边上的高,求∠DBC的度数.
A、下滑时,OP的长度增大 B、上升时,OP的长度减小 C、只要滑动,OP的长度就变化 D、无论怎样滑动,OP的长度不变7. 在△ABC中, ∠C=90°,∠A=∠B,则B=8. 直角三角形ABC中,∠ACB=90°,点D是AB的中点,若AB=10,则CD的长为 .9. 如图,在△ABC中,AB=AC , ∠A=30°,BD是AC边上的高,求∠DBC的度数.
二、能力提升:
-
10. 如图,在△ABC中,∠ACB=90°.分别以点A,B为圆心,以相同的长(大AB)为半径弧,两弧相交于点M和N,作直线MN,交AB于点D,交BC于点E,连结CD.下列结论错误的是( ).
 A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC11. 如图,在中,点在边上,E,F分别是线段 , 的中点.若 , , 则( )
A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC11. 如图,在中,点在边上,E,F分别是线段 , 的中点.若 , , 则( ) A、5 B、6 C、 D、412. 如图,是等腰底边边上的中线, , , 则度数是( )
A、5 B、6 C、 D、412. 如图,是等腰底边边上的中线, , , 则度数是( ) A、 B、 C、 D、13. 两个直角三角形积木 和 按如图所示摆放在水平桌面上, 已知 , , 把下端挂有铅锤的细绳的上端拴在直角顶点 处, 则
A、 B、 C、 D、13. 两个直角三角形积木 和 按如图所示摆放在水平桌面上, 已知 , , 把下端挂有铅锤的细绳的上端拴在直角顶点 处, 则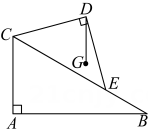 14. 如图,在等腰中, , , D是射线上一点,连结 , 过点A作 , 连结与直线交于点F,若 , 则的长是 .
14. 如图,在等腰中, , , D是射线上一点,连结 , 过点A作 , 连结与直线交于点F,若 , 则的长是 . 15. 如图,在中, , 为上的中线, , 垂足为点E,点F为中点,连接 , , .
15. 如图,在中, , 为上的中线, , 垂足为点E,点F为中点,连接 , , . (1)、求证: .(2)、已知 , 求的度数.16. 如图,和分别位于异侧, , 点O是的中点,连接 , , .
(1)、求证: .(2)、已知 , 求的度数.16. 如图,和分别位于异侧, , 点O是的中点,连接 , , . (1)、若 , , 求的度数:(2)、若锐角 , 求的度数(用的代数式表示).
(1)、若 , , 求的度数:(2)、若锐角 , 求的度数(用的代数式表示).三、拓展创新:
-
17. 在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“智慧三角形”.比如:三个内角分别为100°,50°,30°的三角形是“智慧三角形”,如图∠MON=40°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C.
 (1)、∠ABO=(2)、若∠ACB=60°.求证: △AOC为“智慧三角形”(3)、当△ABC为“智慧三角形”时,请求出∠OAC的度数
(1)、∠ABO=(2)、若∠ACB=60°.求证: △AOC为“智慧三角形”(3)、当△ABC为“智慧三角形”时,请求出∠OAC的度数