湘教版(2024)数学 八年级上册 4.3.4 全等三角形的判定定理(边边边) 同步分层练习
试卷更新日期:2025-08-26 类型:同步测试
一、夯实基础
-
1. 如图,小敏做了一个角平分仪 , 其中 , , 将仪器上的点A与的顶点R重合,调整和 , 使它们分别落在角的两边上,过点A、C画一条射线 , 就是的平分线.此角平分仪的画图原理是( )
 A、 B、 C、 D、2. 如图,工人师傅砌门时,常用木条固定门框 , 使其不变形,这种做法的根据是( )
A、 B、 C、 D、2. 如图,工人师傅砌门时,常用木条固定门框 , 使其不变形,这种做法的根据是( ) A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性3. 如图,在边长为1的正方形网格图中标有A,B,C,D,E,F六个格点.根据图中标示的各点位置,与△ABC全等的是( ).
A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性3. 如图,在边长为1的正方形网格图中标有A,B,C,D,E,F六个格点.根据图中标示的各点位置,与△ABC全等的是( ). A、△ACF B、△ACE C、△BAD D、△CEF4. 如图,已知 , 要证 , 我们将用到全等三角形的判定理或基本事实是( )
A、△ACF B、△ACE C、△BAD D、△CEF4. 如图,已知 , 要证 , 我们将用到全等三角形的判定理或基本事实是( ) A、 B、 C、 D、5. 如图,四边形中,对角线所在的直线是其对称轴,P是直线上的点,下列判断错误的是( )
A、 B、 C、 D、5. 如图,四边形中,对角线所在的直线是其对称轴,P是直线上的点,下列判断错误的是( ) A、 B、 C、 D、6. 在实际生活中,经常用到一些几何图形的稳定性或不稳定性,下列实物图中利用了稳定性的是( )A、伸缩门
A、 B、 C、 D、6. 在实际生活中,经常用到一些几何图形的稳定性或不稳定性,下列实物图中利用了稳定性的是( )A、伸缩门 B、升降机
B、升降机 C、栅栏
C、栅栏 D、椅子
D、椅子 7. 周末小高同学全家去饭店吃饭,他发现饭店房间里放着一个儿童座椅(如图),他观察这个儿童座椅的主体框架成三角形,从而保证儿童坐上去会很安全,这样的设计利用的数学原理是三角形的(填“稳定性”或“不稳定性”).
7. 周末小高同学全家去饭店吃饭,他发现饭店房间里放着一个儿童座椅(如图),他观察这个儿童座椅的主体框架成三角形,从而保证儿童坐上去会很安全,这样的设计利用的数学原理是三角形的(填“稳定性”或“不稳定性”). 8. 如图,若 , , , 则的度数为 .
8. 如图,若 , , , 则的度数为 . 9. 如图是雨伞在开合过程中某时刻的截面图,伞骨 , 点D,E分别是AB,AC的中点,DM,EM是连接弹簧和伞骨的支架,且、已知弹簧M在向上滑动的过程中,总有 , 其判定依据是 .
9. 如图是雨伞在开合过程中某时刻的截面图,伞骨 , 点D,E分别是AB,AC的中点,DM,EM是连接弹簧和伞骨的支架,且、已知弹簧M在向上滑动的过程中,总有 , 其判定依据是 . 10. 如图, , . 求证: .
10. 如图, , . 求证: .
二、能力提升
-
11. 在和中,若有:①;②;③;④;⑤;⑥ , 则下列条件组合中,不能判定的是( )A、①②③ B、①②⑤ C、②④⑤ D、①③⑥12. 如图,这是一个平分角的仪器, , 将点A放在一个角的顶点,使AB、AD分别与这个角的两边重合,可证 , 从而得到AC就是这个角的平分线.其中证明的数学依据是( )
 A、SSS B、ASA C、SAS D、AAS13. 有下列命题:
A、SSS B、ASA C、SAS D、AAS13. 有下列命题:①三个角对应相等的两个三角形全等.
②三条边对应相等的两个三角形全等.
③有两角和其中一个角的对边对应相等的两个三角形全等.
④有两边和一个角对应相等的两个三角形全等.
其中真命题有( ).
A、1个 B、2个 C、3个 D、4个14. 如图,小明做了一个长方形框架,发现很容易变形,请你帮他选择一个最好的加固方案( ) A、
A、 B、
B、 C、
C、 D、
D、 15. 生活中,如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( )
15. 生活中,如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( ) A、稳定性
A、稳定性
B、全等性
C、灵活性
D、对称性16. 如图,在的两边上截取 , . 连接 , 交于点 , 则下列结论正确的是①;②;③;④ .
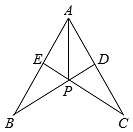 A、①②③④ B、①②③ C、②③④ D、①③④17. 如图,已知AB=AC,AD=AE,BD=EC,则图中有对全等三角形,它们是.
A、①②③④ B、①②③ C、②③④ D、①③④17. 如图,已知AB=AC,AD=AE,BD=EC,则图中有对全等三角形,它们是. 18. 人站在晃动的公共汽车上.若你分开两腿站立,则需伸出一只手去抓栏杆才能站稳,这是利用了 .19. 下列图形中,所有具有稳定性的图形序号是 .
18. 人站在晃动的公共汽车上.若你分开两腿站立,则需伸出一只手去抓栏杆才能站稳,这是利用了 .19. 下列图形中,所有具有稳定性的图形序号是 . 20. 如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若 , 则∠3=°.
20. 如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若 , 则∠3=°. 21. 如图,在与中,E在边上, , , , 若 , 则 .
21. 如图,在与中,E在边上, , , , 若 , 则 . 22. 如图,点在同一直线上,点在直线的同侧,
22. 如图,点在同一直线上,点在直线的同侧,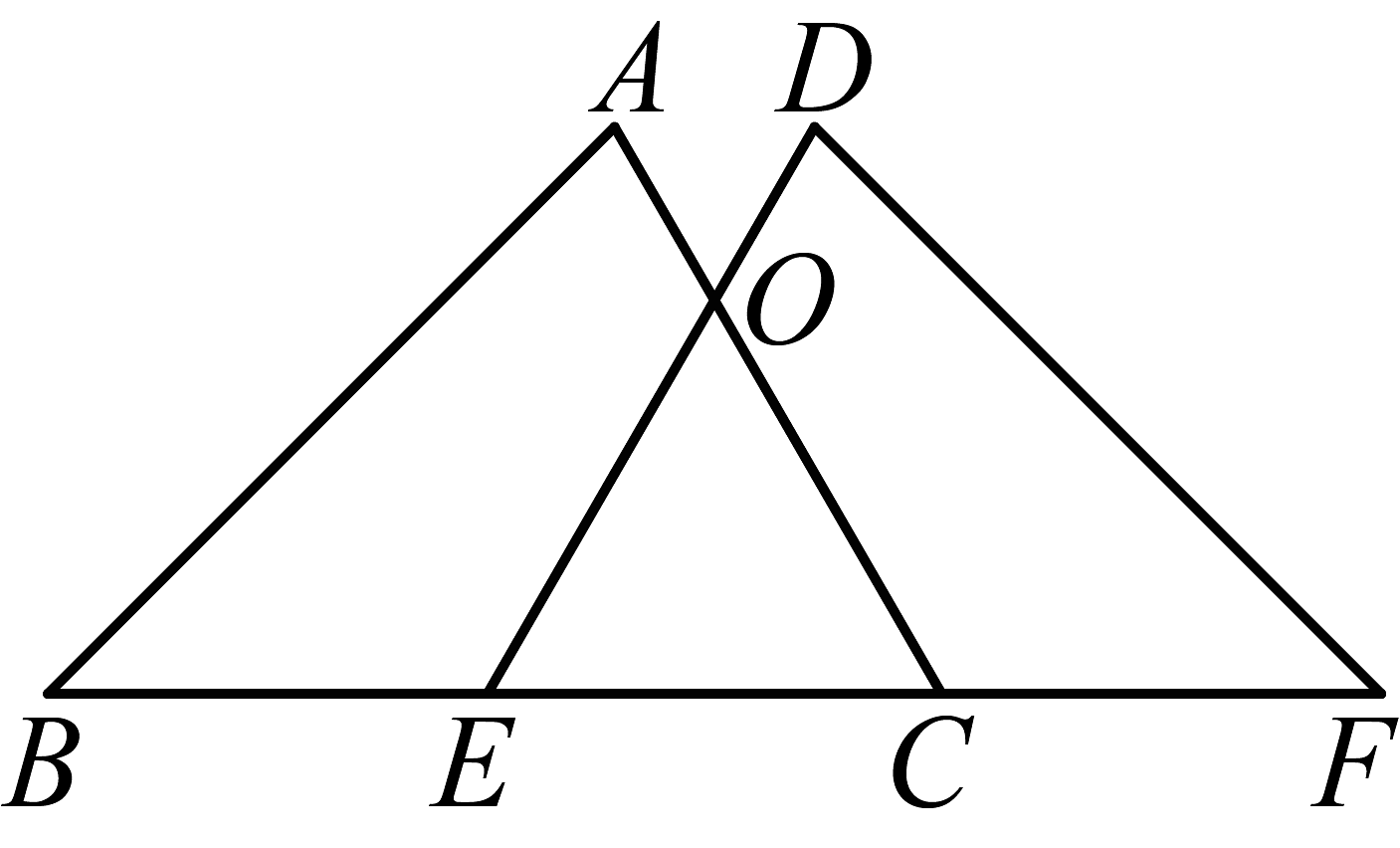 (1)、证明: .(2)、若 , 求的度数.23. 如图所示,已知 , , , 交于点 , 连接 . 试说明: .
(1)、证明: .(2)、若 , 求的度数.23. 如图所示,已知 , , , 交于点 , 连接 . 试说明: .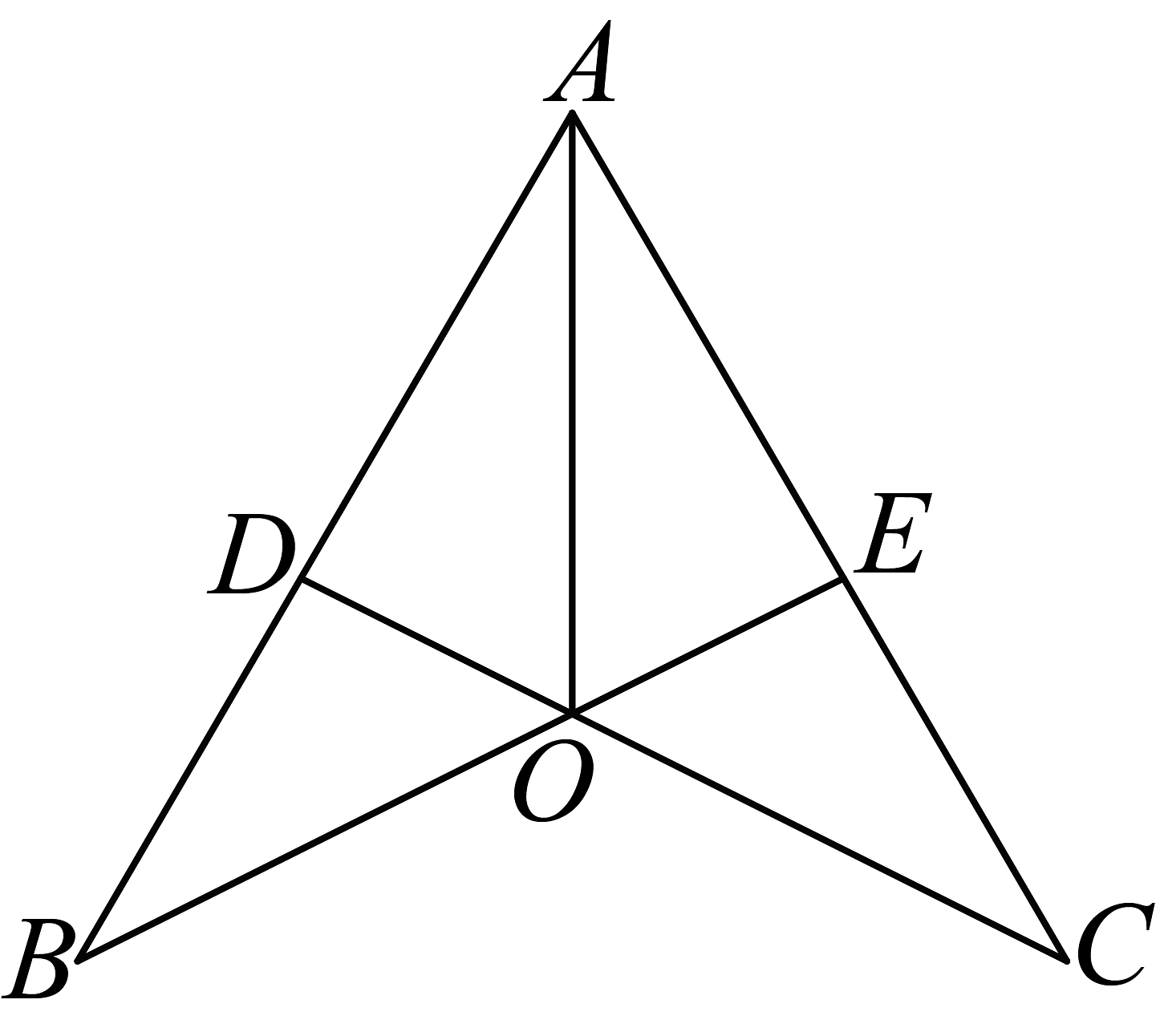
三、拓展提升
-
24. 如图,在和中,在同一条直线上,已知: , 下列给出三个条件: . 解答下列问题:
 (1)、请选择两个合适的作为已知条件,余下一个作为结论,并给出证明过程:
(1)、请选择两个合适的作为已知条件,余下一个作为结论,并给出证明过程:我选择 作为已知条件, 作为结论(填写序号).
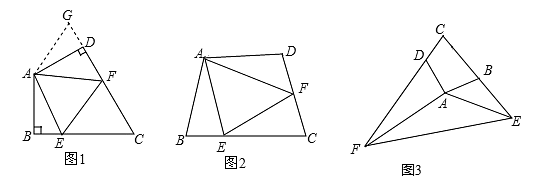
(2)、在(1)的条件下,若与相交于点 , 求 .25. 在四边形中, , 、分别是、上的点,并且 , 试探究图中、、之间的数量关系.【问题提出】
(1)如图1, . 小王同学探究的方法是:延长到点 , 使 . 连接 , 先证明 , 再证明 , 由此可得出结论
【问题探究】
(2)如图2,若 , 上述结论是否仍然成立?请说明理由.
【问题解决】
(3)如图3,若 , 点在的延长线上,点在的延长线上,仍然满足 , 请写出与的数量关系,并给出证明过程.