湘教版(2024)数学 八年级上册 4.3.3 全等三角形的判定定理(角边角、角角边) 同步分层练习
试卷更新日期:2025-08-26 类型:同步测试
一、夯实基础
-
1. 如图,已知 , 添加哪个条件可以证明的是( )
 A、 B、 C、 D、以上都不可以2. 如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带( )去最省事.
A、 B、 C、 D、以上都不可以2. 如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带( )去最省事. A、① B、② C、③ D、①③3. 如图,已知△ABC的三条边和三个角,则下面甲、乙、丙三个三角形中不能证明和 全等的是( )
A、① B、② C、③ D、①③3. 如图,已知△ABC的三条边和三个角,则下面甲、乙、丙三个三角形中不能证明和 全等的是( ) A、甲和乙 B、只有甲 C、只有乙 D、只有丙4. 已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
A、甲和乙 B、只有甲 C、只有乙 D、只有丙4. 已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( ) A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA5. 如图,∠ABC=∠C=90°,AB=BE,AD⊥BE于点D,若BD=3,则CE=.
A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA5. 如图,∠ABC=∠C=90°,AB=BE,AD⊥BE于点D,若BD=3,则CE=. 6. 如图, , , 图中两个三角形是否全等?(填“是”或“否”),如果全等,请写出与边相等的对应边 .
6. 如图, , , 图中两个三角形是否全等?(填“是”或“否”),如果全等,请写出与边相等的对应边 . 7. 如图, , 为的中点,若 , , 则 .
7. 如图, , 为的中点,若 , , 则 . 8. 如图,已知线段AC、BD相交于点E,连接AB、DC、BC,AE=DE,∠A=∠D.求证:△ABE≌△DCE;
8. 如图,已知线段AC、BD相交于点E,连接AB、DC、BC,AE=DE,∠A=∠D.求证:△ABE≌△DCE;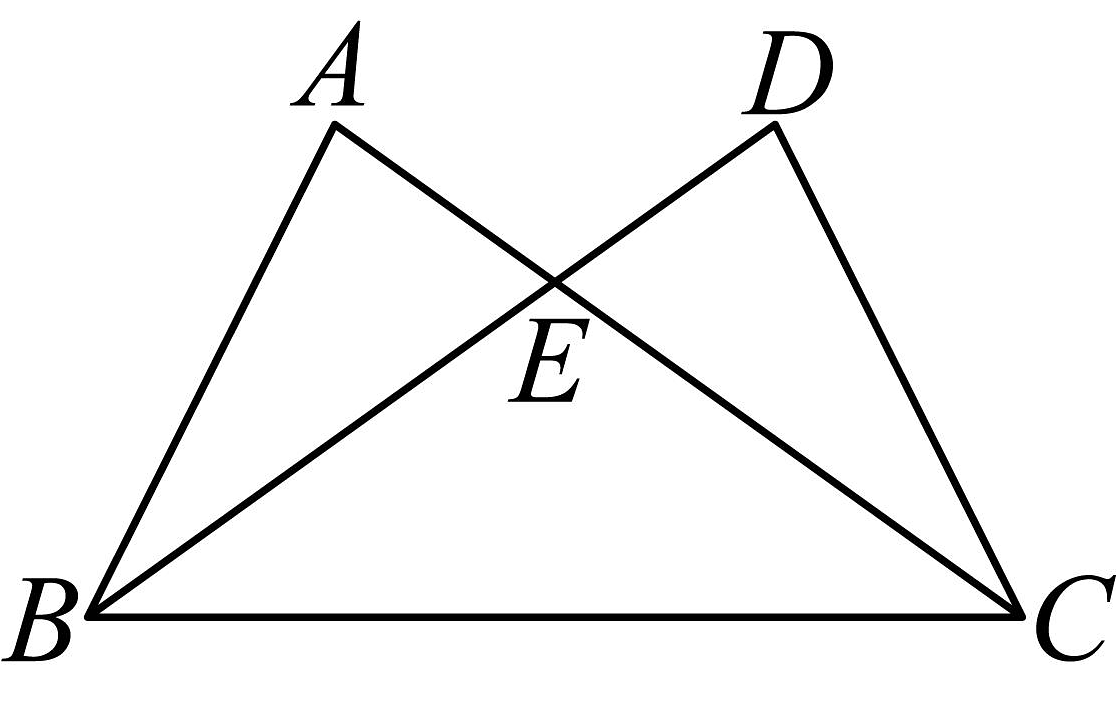 9. 已知:如图, , , , 求证, .
9. 已知:如图, , , , 求证, .
二、能力提升
-
10. 如图,已知 , 添加一个条件不能证明的是( )
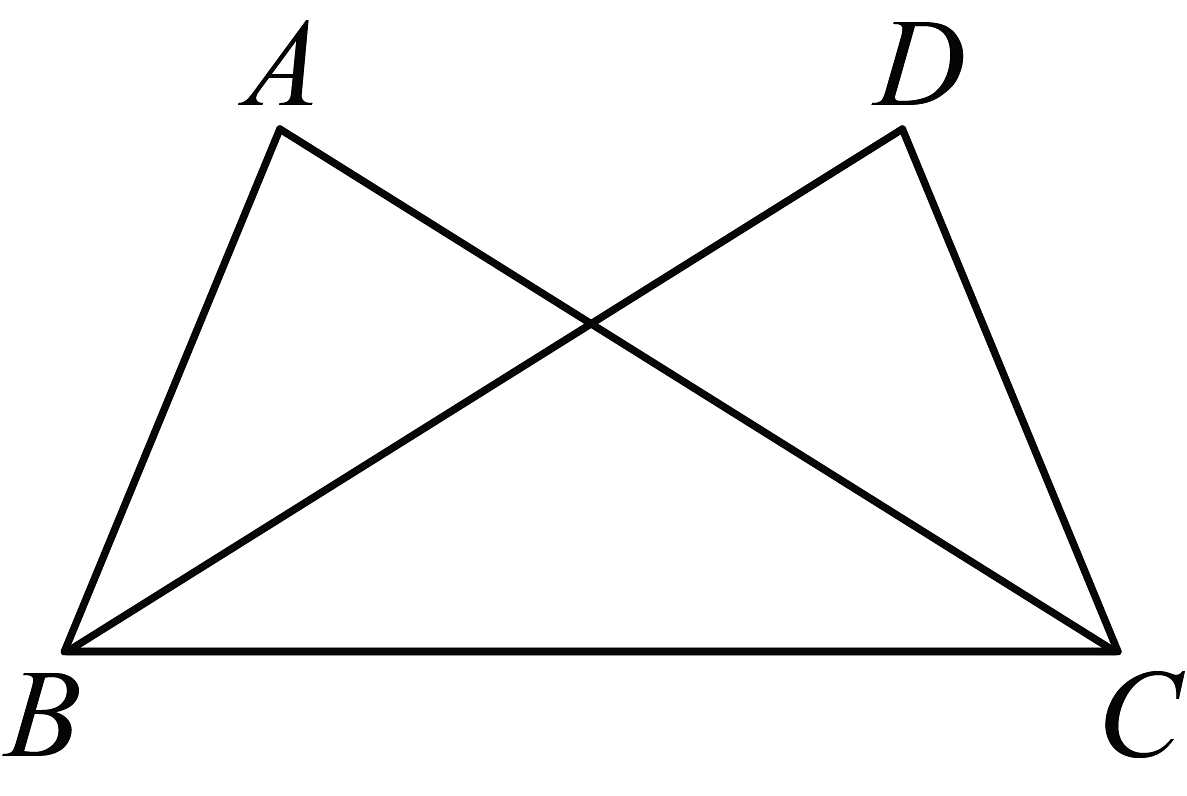 A、 B、 C、 D、11. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是 , 当小明从水平位置CD上升时,这时小红离地面的高度是( )
A、 B、 C、 D、11. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是 , 当小明从水平位置CD上升时,这时小红离地面的高度是( ) A、 B、 C、 D、12. 如图, , , 若 , , 则的长是( )
A、 B、 C、 D、12. 如图, , , 若 , , 则的长是( ) A、5 B、4 C、3 D、5.513. 如图,在中, , 的角平分线交于点D,于点E,若与的周长分别为13和3,则的长为( )
A、5 B、4 C、3 D、5.513. 如图,在中, , 的角平分线交于点D,于点E,若与的周长分别为13和3,则的长为( ) A、10 B、16 C、8 D、514. 如图,已知中, , , 是高和的交点,则线段的长度为( )
A、10 B、16 C、8 D、514. 如图,已知中, , , 是高和的交点,则线段的长度为( ) A、2 B、4 C、5 D、不能确定15. 为测量一池塘两端A,B间的距离.甲、乙两位同学分别设计了两种不同的方案.
A、2 B、4 C、5 D、不能确定15. 为测量一池塘两端A,B间的距离.甲、乙两位同学分别设计了两种不同的方案.甲:如图1,先过点B作的垂线 , 再在射线上取C,D两点,使 , 接着过点D作的垂线 , 交的延长线于点E.则测出的长即为A,B间的距离;
乙:如图2,先确定直线 , 过点B作射线 , 在射线上找可直接到达点A的点D,连接 , 作 , 交直线于点C,则测出的长即为间的距离,则下列判断正确的是( )
 A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行16. 如图,已知的面积为12,平分 , 且于点P,则的面积是 .
A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行16. 如图,已知的面积为12,平分 , 且于点P,则的面积是 . 17. 如图,已知 , , 且 , 那么是的 . (填“中线”或“角平分线”)
17. 如图,已知 , , 且 , 那么是的 . (填“中线”或“角平分线”) 18. 如图,在中, , , 于 , 于 , , , .
18. 如图,在中, , , 于 , 于 , , , . 19. 如图,点A,C,B,D在同一条直线上, . 若 , 则的度数为 .
19. 如图,点A,C,B,D在同一条直线上, . 若 , 则的度数为 . 20. 已知,如图,∠1=∠2,∠C=∠D,BC=BD,求证:ABD≌EBC.
20. 已知,如图,∠1=∠2,∠C=∠D,BC=BD,求证:ABD≌EBC. 21. 如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得 .
21. 如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得 . (1)、求证:;(2)、若 , 求的长度;
(1)、求证:;(2)、若 , 求的长度;三、拓展创新
-
22. 小亮同学在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球 , 小球可以自由摆动,如图,表示小球静止时的位置当小明用发声物体靠近小球时,小球从摆到位置,此时过点作于点 , 当小球摆到位置时,与恰好垂直(图中的、、、在同一平面上),过点作于点 , 测得 , .
 (1)、求证:;(2)、求的长.23. 下面是某数学兴趣小组在项目学习课上的方案策划书,请仔细阅读,并完成相应的任务.
(1)、求证:;(2)、求的长.23. 下面是某数学兴趣小组在项目学习课上的方案策划书,请仔细阅读,并完成相应的任务.项目课题
探究用全等三角形解决“不用直接测量,得到高度”的问题
问题提出
墙上有一点A,在无法直接测量的情况下,如何得到点A的高度?
项目图纸
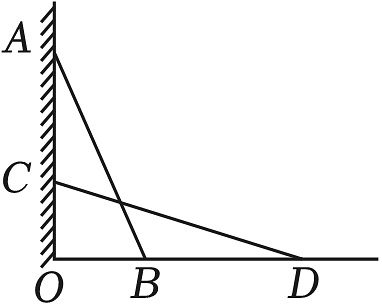
解决过程
①标记测试直杆的底端点 , 测量的长度.②找一根长度大于的直杆,使直杆斜靠在墙上,且顶端与点重合;③使直杆顶端缓慢下滑,直到;④记下直杆与地面的夹角;
项目数据
…
任务:
(1)、由于项目记录员粗心,记录排乱了“解决过程”,正确的顺序应是 ;A.②→③→①→④
B.③→④→①→②
C.①→②→④→③
D.②→④→③→①
(2)、若 , 则 ;(3)、请你说明他们作法的正确性.