湘教版（2024）数学八年级上册 4.3.2 全等三角形的判定定理（边角边) 同步分层练习

试卷更新日期：2025-08-26 类型：同步测试

进入出卷网下载

一、夯实基础

1. 如图， $A C$ 与 $B D$ 交于点O，若 $O A = O D$ ，要用“SAS”证明 $△ A O B ≌ △ D O C$ ，还需要的条件是（）

A、 $O B = O C$ B、 $A B = D C$ C、 $∠ A = ∠ D$ D、 $∠ B = ∠ C$

查看试题解析
2. 下列命题是真命题的是（）

A、三角形的外角大于它的任何一个内角 B、两边及一角对应相等的两个三角形全等 C、满足 $a + b > c$ 的 $a$ 、 $b$ 、 $c$ 三条线段一定能组成三角形 D、对顶角相等

查看试题解析
3. 如图，小明与小敏玩跷跷板游戏，如果跷跷板的支点 $O$ （即跷跷板的中点）至地面的距离是 $45 cm$ ，当小敏从水平位置 $C D$ 下降 $20 cm$ 时，小明离地面的高度是（）

A、 $20 cm$ B、 $45 cm$ C、 $25 cm$ D、 $65 cm$

查看试题解析
4. 如图，将 $△ A B C$ 沿AC对折，点 $B$ 与点 $E$ 重合，则全等的三角形有（）

A、1对 B、2对 C、3对 D、4对

查看试题解析
5. 如图，已知 $A D / / B C$ ，欲用“边角边”证明 $△ A B C$ ≌ $△ C D A$ ，需补充条件（）

A、 $A B = C D$ B、 $∠ B = ∠ D$ C、 $A D = C B$ D、 $∠ B A C = ∠ D C A$

查看试题解析
6. 请规范书写 $S A S$ 的具体内容：．

查看试题解析
7. 如图是边长均为 $1$ 的小正方形网格， $A$ ， $B$ ， $C$ ， $D$ 均在格点上，则 $∠ 1 + ∠ 2 =$ $°$ ．

查看试题解析
8. 两条直角边分别相等的两个直角三角形全等．（填“一定”“不一定”或“一定不”）

查看试题解析
9. 如图，有一座小山，现要在小山A，B的两端开一条隧道，施工队要知道A，B两端的距离，于是先在平地上取一个可以直接到达点A和点B的点C，连接 $A C$ 并延长到D，使 $C D = C A$ ，连接 $B C$ 并延长到E，使 $C E = C B$ ，连接 $D E$ ．经测量 $D E$ ， $E C$ ， $D C$ 的长度分别为 $800 m$ ， $500 m$ ， $400 m$ ，则A，B之间的距离为m；

查看试题解析
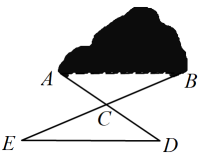10. 如图所示的5个三角形中：△ABC≌ ， △DEF≌ ．

查看试题解析
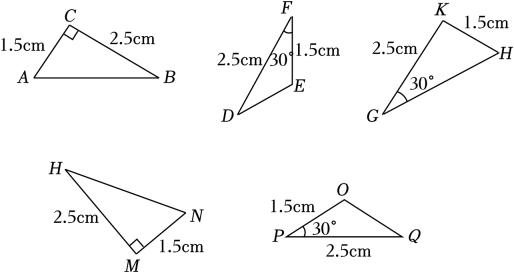11. 如图，点B，C，E，F在同一直线上，点A，D在 $B C$ 的异侧， $A B = D C$ ， $B F = C E$ ， $∠ B = ∠ C$ ．求证： $A E ∥ D F$ ．

查看试题解析
12. 如图，小明自己试着制作风筝，制作了风筝的部分之后发现，可以设计成一道数学题，题目如下：点D、E在 $△ A B C$ 的边 $B C$ 上， $A B = A C$ ， $∠ B A E = ∠ C A D$ ， $A E = A D$ ．求证： $B D = C E$ ．

查看试题解析

二、能力提升

13. 如图，在 $3 \times 3$ 的正方形网格中，点A，B，C，D均为格点，顺次连接 $A B$ ， $B C$ ， $C D$ ， $D A$ ，则下列说法正确的是（）

A、 $∠ B A D = ∠ B C D$ B、 $∠ B A D + ∠ B C D = 45 °$ C、 $∠ A D C = 120 °$ D、 $∠ A B C - ∠ B C D = 90 °$

查看试题解析
14. 如图，在 $△ A B C$ 中，分别延长 $A C, A B$ 边上的中线 $B D, C E$ 到 $F, G$ ．使 $D F = B D, E G = C E$ ，则下列说法：① $G A = A F$ ；② $G A ∥ B C$ ；③ $G B = B F$ ；④四边形 $G B C F$ 的面积是 $△ A B C$ 面积的3倍．其中正确的有（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 4$ ， $B C = 3$ ， $A B = 5$ ， P、D分别是AC、AB上的动点，则 $B P + P D$ 的最小值为（）

A、3 B、 $3.6$ C、 $4.2$ D、 $4.8$

查看试题解析
16. 如图，点P是 $∠ B A C$ 平分线 $A D$ 上的一点， $A C = 7$ ， $A B = 3$ ， $P B = 2$ ，则 $P C$ 的长不可能是（）

A、6 B、5 C、4 D、3

查看试题解析
17. 如图所示， $A B = A C$ ， $A D = A E$ ， $∠ B A C = ∠ D A E$ ， $∠ 1 = 25 °$ ， $∠ 2 = 30 °$ ，则 $∠ 3 =$

查看试题解析
18. 某数学兴趣小组的同学打算测量一个小口圆形容器内径时遇到了困难，小组同学们借用学习过的三角形全等的知识合作制作了特制工具测量器．如图所示，将等长的钢条 $A D$ 和 $B C$ 的中点 $O$ 焊接在一起，制作了一把“ $X$ 形卡钳”．根据“ $X$ 形卡钳”的制作原理能判断 $△ A B O ≌ △ D C O$ ，从而测量出 $A B$ 的长就等于内径 $C D$ 的长．请写出 $△ A B O ≌ △ D C O$ 的理由：．

查看试题解析
19. 如图是由4个相同的小正方形组成的网格图，则 $∠ 1 + ∠ 2 + ∠ 3 =$ ．

查看试题解析
20. 如图， $B O$ 为 $△ A B C$ 的中线，延长 $B O$ 至D，使 $O D = O B$ ，连接 $C D$ ，已知 $B C = 6$ ， $O C - O D = 2$ ，则 $△ A B C$ 与 $△ D O C$ 的周长差是．

查看试题解析
21. $△ A B C$ 中， $A B = 12$ ， $B C$ 边上的中线 $A D = 5$ ，则 $A C$ 的取值范围是．

查看试题解析
22. 如图，已知 $B$ 、 $E$ 、 $C$ 、 $F$ 在同一条直线上， $A B = D E$ ， $A B ∥ D E$ ， $B E = C F$ ， $A C$ 与 $D E$ 交于点 $G$ ．

(1)、求证： $△ A B C ≌ △ D E F$ ；

(2)、若 $∠ B = 50 °$ ， $∠ F = 70 °$ ，求 $∠ E G C$ 的度数．

查看试题解析