人教版(2024)八(上)数学第十四章单元质量检测培优卷
试卷更新日期:2025-08-26 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )A、2 B、2或 C、 或 D、2或 或2. 在平面直角坐标系中,已知点 , , , 如果存在点 , 使和全等,则下列选项中不符合题意的点的坐标是( )A、 B、 C、 D、3. 已知AD是△ABC中BC边上的中线,AB=10,AC=6,则AD的取值范围是( )A、4<AD<16 B、2<AD<8 C、4<AD<10 D、8≤AD≤164. 如图,在平面直角坐标系中,点为轴正半轴上的一点,点、分别在轴的负半轴和正半轴上, , 点为第二象限内一动点,点在的延长线上,交于点 , 且 . 下列结论:①;②平分;③平分;④若 , 则 . 其中结论正确的有( )
 A、①③ B、①②③ C、③④ D、①③④5. 如图所示,在△ABC中,AB=8,点M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于F , 已知CF=10,则AC的长为( )
A、①③ B、①②③ C、③④ D、①③④5. 如图所示,在△ABC中,AB=8,点M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于F , 已知CF=10,则AC的长为( ) A、12 B、11 C、10 D、96. 如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( )
A、12 B、11 C、10 D、96. 如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( ) A、90°﹣α B、90°+α C、90°﹣α D、90°+α7. 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
A、90°﹣α B、90°+α C、90°﹣α D、90°+α7. 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+ ∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )
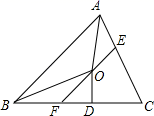 A、①② B、③④ C、①②④ D、①③④8. 如图,△ABC中,∠ACF、∠EAC的角平分线CP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF.则下列结论中正确的个数( )
A、①② B、③④ C、①②④ D、①③④8. 如图,△ABC中,∠ACF、∠EAC的角平分线CP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF.则下列结论中正确的个数( )
①BP平分∠ABC; ②∠ABC+2∠APC=180°;
③∠CAB=2∠CPB;
A、1个 B、2个 C、3个 D、4个9. 如图,在中, , 是的角平分线,点在上,过点作于点 , 延长至 , 使 , 连接交于点 , 平分 , 交的延长线于点 , 连接 , , , 若 . 有下列结论:①;②;③;④ . 其中正确的是( ) A、①②③ B、①②③④ C、①② D、①③④10. 数学课上,老师给出了如下问题:
A、①②③ B、①②③④ C、①② D、①③④10. 数学课上,老师给出了如下问题:如图1, , 是的中点,平分 , 求证: .
小明是这样想的:要证明 , 只需要在上找到一点 , 再试图说明 , 即可.如图2,经过思考,小明给出了以下3种辅助线的添加方式.
①过点作交于点;
②作 , 交于点;
③在上取一点 , 使得 , 连接;
上述3种辅助线的添加方式,可以证明“”的有( )
 A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角 ∠ACD和∠ABC的平分线交于点E,则∠AEB=︒
 12. 在中, , , 分别是 , 边上一点, , , , , , 则的长 . (用含 , , 的式子表示)
12. 在中, , , 分别是 , 边上一点, , , , , , 则的长 . (用含 , , 的式子表示) 13. 如图,在中,和的平分线相交于点交于交于F,过点O作于D,下列三个结论:①;②当时,;③若 , , 则 . 其中正确的是 . (填序号)
13. 如图,在中,和的平分线相交于点交于交于F,过点O作于D,下列三个结论:①;②当时,;③若 , , 则 . 其中正确的是 . (填序号) 14. 如图,点D是△ABC三条角平分线的交点,∠ABC=68°,若AB+BD=AC , 则∠ACB的度数为 .
14. 如图,点D是△ABC三条角平分线的交点,∠ABC=68°,若AB+BD=AC , 则∠ACB的度数为 . 15. 三个全等三角形按如图的形式摆放,则的度数是.
15. 三个全等三角形按如图的形式摆放,则的度数是.
三、解答题:本大题共8小题,共75分.
-
16. 如图1,点A、D在y轴正半轴上,点B、C在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=90°-∠BDO.
 (1)、求证:AC=BC;(2)、如图2,点C的坐标为(4,0),点E为AC上一点,且AD= DE,求BC+EC的长;(3)、在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当H在FC上移动、点G点在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.17. 如图:在四边形中, , , , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系.
(1)、求证:AC=BC;(2)、如图2,点C的坐标为(4,0),点E为AC上一点,且AD= DE,求BC+EC的长;(3)、在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当H在FC上移动、点G点在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.17. 如图:在四边形中, , , , 分别是 , 上的点,且 , 探究图中线段 , , 之间的数量关系. (1)、小王同学探究此问题的方法是:延长到点 , 使 , 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是 ;(直接写结论,不需证明)(2)、如图 , 若在四边形中, , , 分别是、上的点,且 , ()中结论是否仍然成立,并说明理由;(3)、如图 , 在四边形中, , , 分别是边、延长线上的点,且 , ()中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.18.
(1)、小王同学探究此问题的方法是:延长到点 , 使 , 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是 ;(直接写结论,不需证明)(2)、如图 , 若在四边形中, , , 分别是、上的点,且 , ()中结论是否仍然成立,并说明理由;(3)、如图 , 在四边形中, , , 分别是边、延长线上的点,且 , ()中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.18. (1)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC , 直线l经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E.证明:DE=BD+CE.(2)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC , D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点I , 求证:I是EG的中点.19. 问题引入:课外兴趣小组活动时,老师提出这样的问题:如图1,在△ABC中,AB=5,AC=3,求BC边上的中线的取值范围.
(1)、某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC , 直线l经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E.证明:DE=BD+CE.(2)、组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC , D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点I , 求证:I是EG的中点.19. 问题引入:课外兴趣小组活动时,老师提出这样的问题:如图1,在△ABC中,AB=5,AC=3,求BC边上的中线的取值范围.小华在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE,把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.从中他总结出:解题时,条件中若出现“中线”“中点”等条件,可以考虑将中线加倍延长,构造全等三角形,把分散的条件和需求证的结论集中到同一个三角形中.
 (1)、请你用小华的方法证明AB+AC>2AD;(2)、由第(1)问方法的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的一点,AE是△ABD的中线,CD=AB,∠BDA=∠BAD,求证:AC=2AE;(3)、如图3,在Rt△ABO和Rt△CDO中,∠AOB=∠COD=90°,OA=OB,OC=OD,连接AD,点M为AD中点,连接OM,请你直接写出的值.20. 平面直角坐标系中,点 , 分别是轴和轴上的动点, , .
(1)、请你用小华的方法证明AB+AC>2AD;(2)、由第(1)问方法的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的一点,AE是△ABD的中线,CD=AB,∠BDA=∠BAD,求证:AC=2AE;(3)、如图3,在Rt△ABO和Rt△CDO中,∠AOB=∠COD=90°,OA=OB,OC=OD,连接AD,点M为AD中点,连接OM,请你直接写出的值.20. 平面直角坐标系中,点 , 分别是轴和轴上的动点, , . (1)、如图 , 若 , , 求点的坐标;(2)、如图 , 设交轴于点 , 若平分 , , 求点的纵坐标;(3)、如图 , 当点运动到原点时,的平分线交轴于点 , 为线段上一点,将沿翻折,的对应边的延长线交于点 , 为线段上一点,且 , 求的值.(用含的式子表示)21. 【问题情境】
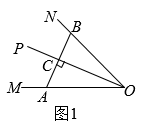
(1)、如图 , 若 , , 求点的坐标;(2)、如图 , 设交轴于点 , 若平分 , , 求点的纵坐标;(3)、如图 , 当点运动到原点时,的平分线交轴于点 , 为线段上一点,将沿翻折,的对应边的延长线交于点 , 为线段上一点,且 , 求的值.(用含的式子表示)21. 【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP平分 . 点A为OM上一点,过点A作 , 垂足为C,延长AC交ON于点B,可根据ASA证明 , 则 , (即点C为AB的中点).
 (1)、问题探究:如图2,中, , , CD平分 , , 垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论:
(1)、问题探究:如图2,中, , , CD平分 , , 垂足E在CD的延长线上,试探究BE和CD的数量关系,并证明你的结论: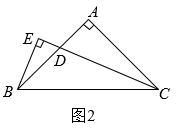 (2)、拓展延伸:如图3,中, , , 点D在线段BC上,且 , 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.
(2)、拓展延伸:如图3,中, , , 点D在线段BC上,且 , 于E,DE交AB于F,试探究BE和DF之间的数量关系,并证明你的结论.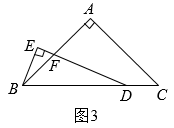 22. 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.
22. 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE. (1)、如图1,过F点作FG⊥AC交于G点,求证:AG=EC;(2)、如图2,连接BF交AC于G点,若AC=BC=4,AG=3,求证:E点为BC中点;(3)、如图3,当E点在CB的延长线上时,连接BF与AC的延长线交于D点,若 , 求的值是 .23. 综合与实践,如图,已知 , 直线与交于点 , 与交于点 , 射线和射线交于点 .
(1)、如图1,过F点作FG⊥AC交于G点,求证:AG=EC;(2)、如图2,连接BF交AC于G点,若AC=BC=4,AG=3,求证:E点为BC中点;(3)、如图3,当E点在CB的延长线上时,连接BF与AC的延长线交于D点,若 , 求的值是 .23. 综合与实践,如图,已知 , 直线与交于点 , 与交于点 , 射线和射线交于点 . (1)、若平分平分 , 则;(2)、若 , 则;(3)、将(2)中“”改为“”,其余条件不变,求的度数(用含的代数式表示);(4)、若将分成两部分,也将分成两部分, , 则的度数(用含的代数式表示).
(1)、若平分平分 , 则;(2)、若 , 则;(3)、将(2)中“”改为“”,其余条件不变,求的度数(用含的代数式表示);(4)、若将分成两部分,也将分成两部分, , 则的度数(用含的代数式表示).