1.5三角形全等的判定（培优卷）-浙教版（2024）数学八（上）进阶同步练

试卷更新日期：2025-08-24 类型：同步测试

进入出卷网下载

一、选择题

1. 观察用直尺和圆规作一个角等于已知角的示意图，能得出 $∠ C P D = ∠ A O B$ 的依据是（）．

A、由“等边对等角”可得 $∠ C P D = ∠ A O B$ B、由 $S S S$ 可得 $△ O G H$ $≌$ $△ P M N$ ，进而可证 $∠ C P D = ∠ A O B$ C、由 $S A S$ 可得 $△ O G H$ $≌$ $△ P M N$ ，进而可证 $∠ C P D = ∠ A O B$ D、由 $A S A$ 可得 $△ O G H$ $≌$ $△ P M N$ ，进而可证 $∠ C P D = ∠ A O B$

查看试题解析
2. 两组邻边分别相等的四边形叫作“筝形”.如图，四边形ABCD 是一个筝形，其中AD=CD，AB=CB.小明在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO=CO= $\frac{1}{2}$ AC；③△ABD≌△CBD.其中正确的结论有( ).

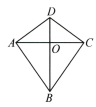A、0个 B、1 个 C、2个 D、3个

查看试题解析
3. 如图，已知 $∠ B O P$ 与 $O P$ 上的点C，点A，小临同学现进行如下操作：①以点O为圆心， $O C$ 长为半径画弧，交 $O B$ 于点D，连接 $C D$ ；②以点A为圆心， $O C$ 长为半径画弧，交 $O A$ 于点M；③以点M为圆心， $C D$ 长为半径画弧，交第2步中所画的弧于点E，连接 $M E$ ．下列结论不能由上述操作结果得出的是（　　）

A、 $∠ O D C = ∠ A E M$ B、 $O B ∥ A E$ C、 $∠ A M E = 2 ∠ A O D$ D、 $C D ∥ M E$

查看试题解析
4. 在 $△ A B C$ 和 $△ A^{'} B^{'} C^{'}$ 中，若有：① $A B = A^{'} B^{'}$ ；② $B C = B^{'} C^{'}$ ；③ $A C = A^{'} C^{'}$ ；④ $∠ A = ∠ A^{'}$ ；⑤ $∠ B = ∠ B^{'}$ ；⑥ $∠ C = ∠ C^{'}$ ，则下列条件组合中，不能判定 $△ A B C ≌ △ A^{'} B^{'} C^{'}$ 的是（）

A、①②③ B、①②⑤ C、②④⑤ D、①③⑥

查看试题解析
5. 如图，CD⊥AB，BE⊥AC，垂足分别为D，E，BE与CD相交于点O，∠1=∠2.图中全等三角形共有( ).

A、2对 B、3对 C、4对 D、5对

查看试题解析
6. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ，连接 $B D$ ，取 $B E = A D$ ，连接 $C E$ ，下列条件中不一定能判定 $Δ A B D ≅ Δ E C B$ 的是 $($ $)$

A、 $B D = C B$ B、 $A B = E C$ C、 $∠ A B C = ∠ D E C$ D、 $∠ A B D = ∠ E C B$

查看试题解析
7. 如图，在 $△ A C B$ 中， $∠ A C B = 90 °$ ， $△ A B C$ 的角平分线 $A D$ 、 $B E$ 相交于点 $P$ ，过 $P$ 作 $P F ⊥ A D$ 交 $B C$ 的延长线于点 $F$ ，交 $A C$ 于点 $H$ ．有下列结论：① $∠ A P B = 135 °$ ；② $△ A B P ≌ △ F B P$ ；③ $∠ A H P = ∠ A B C$ ；④ $A H + B D = A B$ ；其中正确的个数是（　　）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
8. 如图，在 $△ A B C$ 中 $A B = A C$ ， $∠ B = ∠ A C D = 45 °$ ， D，E是BC上两点，且 $∠ D A E = 45 °$ ，过点A作 $A F ⊥ A D$ ，垂足是A，过点C作 $C F ⊥ B C$ ，垂足是C，CF交AF于点F，连接EF．给出下列结论：① $△ A B D ≌ △ A C F$ ；② $D E = E F$ ；③若 $S_{△ A D E} = 10$ ， $S_{△ C E F} = 4$ ，则 $S_{△ A B C} = 24$ ；④ $B D + C E = D E$ ．其中正确结论的字号是（）

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析

二、填空题

9. 如图，在 $△ A B C$ 中，已知 $A D$ 平分 $∠ B A C$ ，且 $A D ⊥ B D$ 于点D， $△ A D C$ 的面积是8，则 $△ A B C$ 的面积是．

查看试题解析
10. 如图，AB⊥CD，且AB=CD，E，F是AD上两点，CE⊥AD，BF⊥AD.若CE=a，BF=b，EF=c，则AD的长为.

查看试题解析
11. 在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $E$ ， $D$ 分别是 $A B$ ， $A C$ 边上一点， $A B = A D$ ， $∠ E D C = ∠ D B C + 135 °$ ， $A B = a$ ， $A C = b$ ， $B C = c$ ，则 $E B$ 的长．（用含 $a$ ， $b$ ， $c$ 的式子表示）

查看试题解析
12. 已知，四边形 $A B C D$ 和四边形 $A^{'} B^{'} C^{'} D^{'}$ 中， $A B = A^{'} B^{'}$ ， $B C = B^{'} C^{'}$ ， $∠ B = ∠ B^{'}$ ， $∠ C = ∠ C^{'}$ ，现在只需补充一个条件，就可得四边形 $A B C D ≌$ 四边形 $A^{'} B^{'} C^{'} D^{'}$ ，下列四个条件：① $∠ A = ∠ A^{'}$ ；② $∠ D = ∠ D^{'}$ ；③ $A D = A^{'} D^{'}$ ；④ $C D = C^{'} D^{'}$ ，其中，符合要求的条件的有．（填所有正确结论的序号）

查看试题解析

三、解答题

13. 如图1，已知△ABC ，过点C作CD∥AB ，且CD＝BC.用尺规作△ECD≌△ABC ， E是边BC上一点.
小瑞：如图2．以点C为圆心，AB长为半径作弧，交BC于点E ，连结DE ，则△ECD≌△ABC ．
小安：以点D为圆心，AC长为半径作弧，交BC于点E ，连结DE ，则△ECD≌△ABC ．
小瑞：小安，你的作法有问题．
小安：哦…我明白了！

(1)、指出小安作法中存在的问题．

(2)、证明：△ECD≌△ABC.

查看试题解析
14.

(1)、模型的发现：
如图 $1$ ，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，直线 $l$ 经过点 $A$ ，且 $B$ ， $C$ 两点在直线 $l$ 的同侧， $B D ⊥$ 直线 $l$ ， $C E ⊥$ 直线 $l$ ，垂足分别为点 $D$ 、 $E .$ 问： $D E$ 、 $B D$ 和 $C E$ 的数量关系．

(2)、模型的迁移：位置的改变
如图 $2$ ，在 $(1)$ 的条件下，若 $B$ 、 $C$ 两点在直线 $l$ 的异侧，请说明 $D E$ 、 $B D$ 和 $C E$ 的数量关系，并证明．

查看试题解析
15. 如图 $1$ ， $∠ A C B = 90 °$ ， $A C = B C$ ， $B E ⊥ C E$ ， $A D ⊥ C E$ 于 $D$ ，

(1)、求证： $△ B C E$ ≌ $△ C A D$ ；

(2)、猜想： $A D$ ， $D E$ ， $B E$ 的数量关系为 $($ 不需证明 $)$ ；

(3)、当 $C E$ 绕点 $C$ 旋转到图 $2$ 位置时，猜想线段 $A D$ ， $D E$ ， $B E$ 之间又有怎样的数量关系，并证明你的结论．

查看试题解析
16. 阅读与思考
下面是小明同学的数学学习笔记，请您仔细阅读并完成相应的任务：构造全等三角形解决图形与几何问题.
在图形与几何的学习中，常常会遇到一些问题无法直接解答，需要添加辅助线才能解决．比如下面的题目中出现了角平分线和垂线段，我们可以通过延长垂线段与三角形的一边相交构造全等三角形，运用全等三角形的性质解决问题．

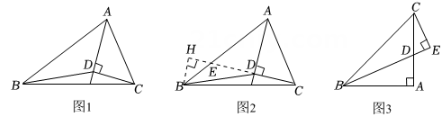
例：如图1，D是△ABC内一点，且AD平分∠BAC ， CD⊥AD ，连结BD ，若△ABD的面积为10，求△ABC的面积．
该问题的解答过程如下：
解：如图2，过点B作BH⊥CD交CD延长线于点H ， CH ， AB交于点E ，
∵AD平分∠BAC ， ∴∠DAB＝∠DAC ． ∵AD⊥CD ， ∴∠ADC＝∠ADE＝90°．
在△ADE和△ADC中， $\{\begin{array}{l} ∠ D A E = ∠ D A C \\ A D = A D \\ ∠ A D E = ∠ A D C \end{array}$ ， ∴△ADE≌△ADC（依据1）
∴ED＝CD（依据2），S_△_ADE＝S_△_ADC ， ∵ $S_{△ B D E} = \frac{1}{2} D E \cdot B H$ ， $S_{△ B D C} = \frac{1}{2} C D \cdot B H$ ．
…

(1)、任务一：上述解答过程中的依据1是，依据2是.

(2)、任务二：请将上述解答过程的剩余部分补充完整.

(3)、应用：如图3，在△ABC中，∠BAC＝90°，AB＝AC ， BE平分∠CBA交AC于点D ，过点C作CE⊥BD交BD延长线于点E ．若CE＝6，求BD的长．

查看试题解析

17. 下表是小聪同学开展项目化学习时填写了部分内容的记录表，

项目：测量小山坡的宽度.

活动：小山坡的宽度不能直接测量，可以借助一些工具，比如：皮尺，直角三角板，测角仪

标杆等，各组确定方案后，选择测量工具，画出测量示意图，再进行实地测量，得到具体数据，从而计算出小山坡的宽度.

成果：下面是小聪同学所在小组进行交流展示的部分项目研究内容：

项目

示意图

测量方案

测得数据

测量小山坡

的宽度AB

在小山坡外面的平地上找一点O，立一根标杆，然后再找到点C，D，使OC=OA.

OD =OB

OA=OC=200 m，OB=OD=250 m，CD =360 m

请你帮助小聪组完成下列任务.

(1)、任务1：王老师发现小聪组的测量方案有问题，请你帮助小聪组找到问题并完善测量方案.

(2)、任务2：完善方案后请你借助上述测量数据，计算小山坡的宽度AB，并说明理由

(3)、任务3：利用所学知识，请你再设计一个测量方案，并简要说明你的设计思路.

查看试题解析

18.

(1)、某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC ，直线l经过点A ， BD⊥直线l ， CE⊥直线l ，垂足分别为点D、E ．证明：DE＝BD+CE ．

(2)、组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC ， D ， A ， E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α ，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

(3)、数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点I ，求证：I是EG的中点．

查看试题解析