1.3证明-浙教版(2024)数学八(上)进阶同步练
试卷更新日期:2025-08-24 类型:同步测试
一、选择题
-
1. 如图,∠1=100°,∠C=70°,则∠A的大小是( )
 A、10° B、20° C、30° D、80°2. 如图,将三角形纸板直角顶点放在直尺上,∠1=35°,∠2=69°,则∠3的度数为( )
A、10° B、20° C、30° D、80°2. 如图,将三角形纸板直角顶点放在直尺上,∠1=35°,∠2=69°,则∠3的度数为( ) A、34° B、35° C、69° D、104°3. 如图,平分 , 求证:.以下是排乱的证明过程:
A、34° B、35° C、69° D、104°3. 如图,平分 , 求证:.以下是排乱的证明过程:
①(已知),
②平分(已知),
③(角平分线的定义),
④(两直线平行,同位角相等),
⑤(等量代换).
证明步㵵顺序正确的是( )
A、③②①④⑤ B、①④②③⑤ C、①③④②⑤ D、①④③②⑤4. 在证明过程中,作为逻辑推理依据最全的是( )A、基本事实、定理 B、定义、基本事实、定理 C、基本事实、定理、题设(已知条件) D、定义、基本事实、定理、题设(已知条件)5. 将一副直角三角板按如图所示方式摆放,含角的三角板的斜边经过含角的三角板的直角顶点,短的直角边与含角的三角板的斜边重合,则为( ) A、 B、 C、 D、6. 如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A、 B、 C、 D、6. 如图,∠ACD=120°,∠B=20°,则∠A的度数是( ) A、120° B、90° C、100° D、30°7. 甲、乙、丙、丁四位同学在操场上踢足球,不小心打碎了玻璃窗.老师问他们是谁打碎了玻璃窗.
A、120° B、90° C、100° D、30°7. 甲、乙、丙、丁四位同学在操场上踢足球,不小心打碎了玻璃窗.老师问他们是谁打碎了玻璃窗.甲说:“是丙,也可能是丁打碎的.”
乙说:“一定是丁打碎的.”
丙说:“我没有打碎玻璃窗.”
丁说:“我没有干这件事.”
若四位同学中只有一位说了谎话,由此我们可以推断,打碎玻璃的同学是( )
A、甲 B、乙 C、丙 D、丁8. 如果甲同学的语文分数或英语分数至少有一门比乙同学高,则称甲同学不亚于乙同学.在班级45个学生中,如果某同学不亚于其他44人,就称他(她)为“潜力之星”,那么某班45个学生中的“潜力之星”最多可能有( )A、22人 B、23人 C、44人 D、45人二、填空题
-
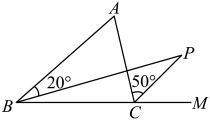
9. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P=.
 10. 结合下图,用符号语言表达定理“同位角相等,两直线平行”的推理形式:
10. 结合下图,用符号语言表达定理“同位角相等,两直线平行”的推理形式:
∵ ,∴a∥b.
 11. 已知:如图,△ABC的两条高线BE,CF相交于点O。
11. 已知:如图,△ABC的两条高线BE,CF相交于点O。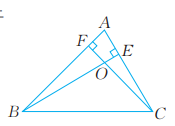
求证:∠BOC=180°-∠A(填空)。
证明:因为BE,CF是△ABC的两条高线( ),
所以∠OEC=∠BFC=90°()。
因为∠ACF+∠A=∠BFC=90°(),
所以∠ACF=90°-∠A。
所以
12. 小明沿街心公园的环形跑道从起点出发按逆时针方向跑步,他用软件记录了跑步的轨迹,他每跑1km软件会在运动轨迹上标注相应的路程,前5 km 的记录如图所示.已知该环形跑道一圈的周长大于1km.小明恰好跑3圈时,路程5km?(填“超过”或“不超过”)
三、解答题
-
13.
 (1)、如图,若∠α=∠β,则AB∥CD.这个命题是真命题还是假命题?(2)、若上述命题是真命题,请说明理由;若上述命题是假命题,请再添加一个条件,使该命题成为真命题,并说明理由.14. 将下列证明过程补充完整:
(1)、如图,若∠α=∠β,则AB∥CD.这个命题是真命题还是假命题?(2)、若上述命题是真命题,请说明理由;若上述命题是假命题,请再添加一个条件,使该命题成为真命题,并说明理由.14. 将下列证明过程补充完整:已知:如图,点分别在上,分别交于点 , .
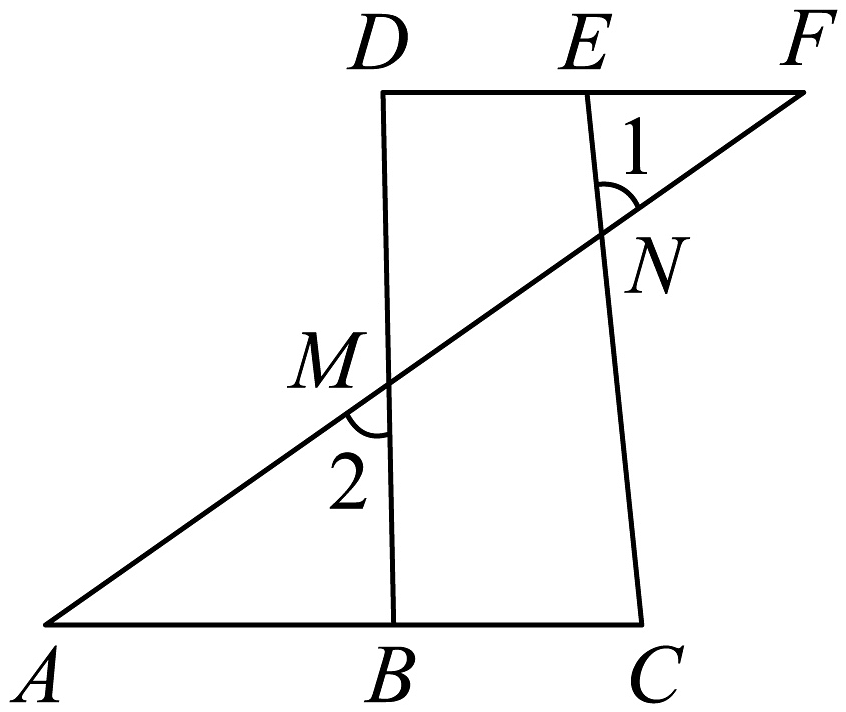
求证: .
证明:因为(已知)
又因为(____________),
所以___________(等量代换).
所以( )
所以(____________).
又因为(已知),
所以(____________).
所以__________( ).
所以( ).
15. 填空:如图,于 , 于 , , 可得平分 .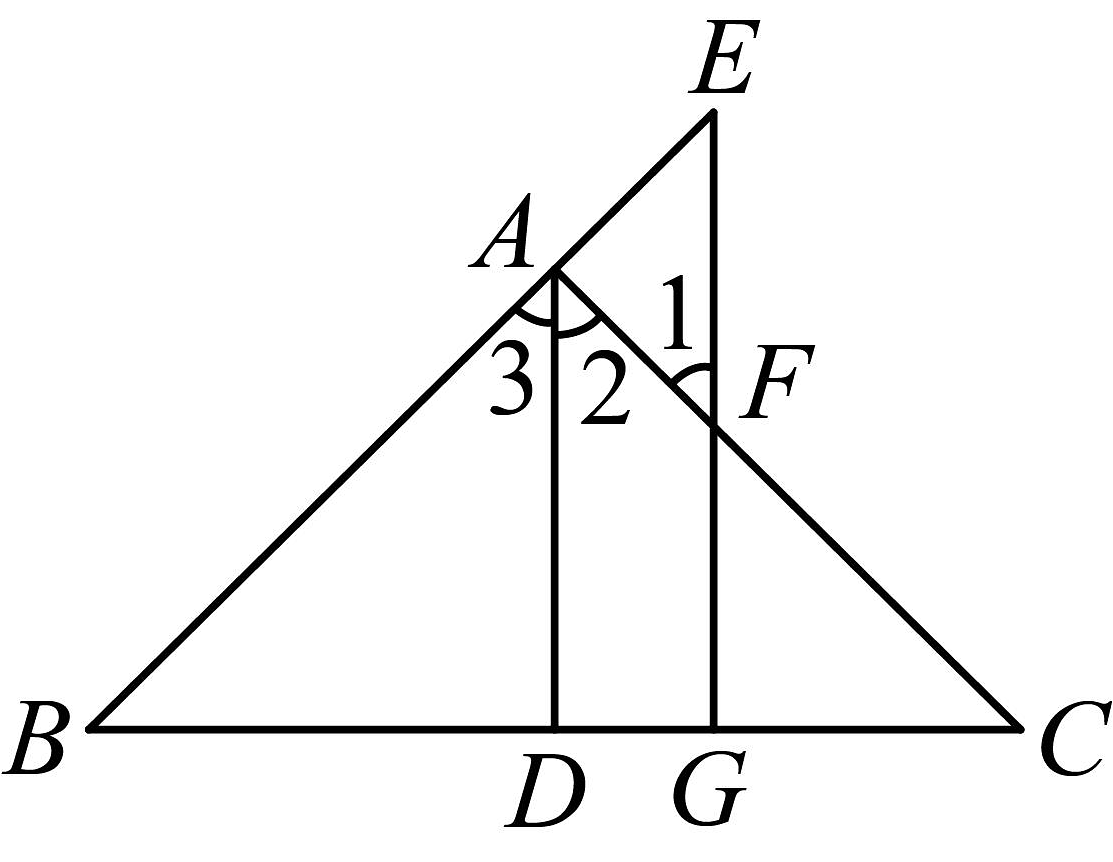
理由如下:
于 , 于(已知),
(______).
(______).
(______),
.
又(______),
(______).
平分(______).
16. 已知:如图,直线a,b被直线c所截,且.求证: a∥b.

你有几种证明方法?
17. 如图,点 , 分别在直线 , 上,连接 , , , 分别与 , 相交于点 , , , . (1)、求证:;(2)、求证: .(3)、若 , 求的度数.
(1)、求证:;(2)、求证: .(3)、若 , 求的度数.
 三角形内角和定理:三角形三个内角和等于180°,
三角形内角和定理:三角形三个内角和等于180°,