高考一轮复习:万有引力与航天
试卷更新日期:2025-08-24 类型:一轮复习
一、选择题
-
1. 卫星a、b绕质量为M的中心天体做圆周运动运动,如图所示,a的轨道半径比b乙的小。忽略两行星之间的万有引力作用,下列说法正确的是( )
 A、卫星a、b运动的周期 B、卫星a、b运动的线速度 C、卫星a、b运动的角速度 D、卫星a、b运动的向心加速度2. 一颗绕太阳运行的小行星,其轨道近日点和远日点到太阳的距离分别约为地球到太阳距离的5倍和7倍。关于该小行星,下列说法正确的是( )A、公转周期约为6年 B、从远日点到近日点所受太阳引力大小逐渐减小 C、从远日点到近日点线速度大小逐渐减小 D、在近日点加速度大小约为地球公转加速度的3. 北斗三号导航卫星系统由三种不同轨道的卫星组成,即24颗地球中圆轨道卫星(轨道形状为圆形,轨道半径在3万公里与1000公里之间)、3颗地球同步轨道卫星和3颗倾斜地球同步轨道卫星。(同步卫星离地高度约为5.6R地 , R地=6.4×103km)则关于地球中圆轨道卫星,下列说法正确的是( )A、比地球同步轨道卫星的线速度大 B、比地球同步轨道卫星的角速度小 C、比地球同步轨道卫星的周期大 D、线速度大于第一宇宙速度4. 2024年10月30日,神舟十九号载人飞船将三名航天员送入太空,飞船入轨后按照预定程序与天和核心舱对接。飞船与核心舱对接过程的示意图如图所示。飞船从圆轨道Ⅰ,通过变轨后,沿椭圆轨道Ⅱ由A处运动到B处,与沿圆轨道Ⅲ运行的核心舱对接,对接后的组合体继续在圆轨道Ⅲ上运行。在上述过程中,飞船( )
A、卫星a、b运动的周期 B、卫星a、b运动的线速度 C、卫星a、b运动的角速度 D、卫星a、b运动的向心加速度2. 一颗绕太阳运行的小行星,其轨道近日点和远日点到太阳的距离分别约为地球到太阳距离的5倍和7倍。关于该小行星,下列说法正确的是( )A、公转周期约为6年 B、从远日点到近日点所受太阳引力大小逐渐减小 C、从远日点到近日点线速度大小逐渐减小 D、在近日点加速度大小约为地球公转加速度的3. 北斗三号导航卫星系统由三种不同轨道的卫星组成,即24颗地球中圆轨道卫星(轨道形状为圆形,轨道半径在3万公里与1000公里之间)、3颗地球同步轨道卫星和3颗倾斜地球同步轨道卫星。(同步卫星离地高度约为5.6R地 , R地=6.4×103km)则关于地球中圆轨道卫星,下列说法正确的是( )A、比地球同步轨道卫星的线速度大 B、比地球同步轨道卫星的角速度小 C、比地球同步轨道卫星的周期大 D、线速度大于第一宇宙速度4. 2024年10月30日,神舟十九号载人飞船将三名航天员送入太空,飞船入轨后按照预定程序与天和核心舱对接。飞船与核心舱对接过程的示意图如图所示。飞船从圆轨道Ⅰ,通过变轨后,沿椭圆轨道Ⅱ由A处运动到B处,与沿圆轨道Ⅲ运行的核心舱对接,对接后的组合体继续在圆轨道Ⅲ上运行。在上述过程中,飞船( )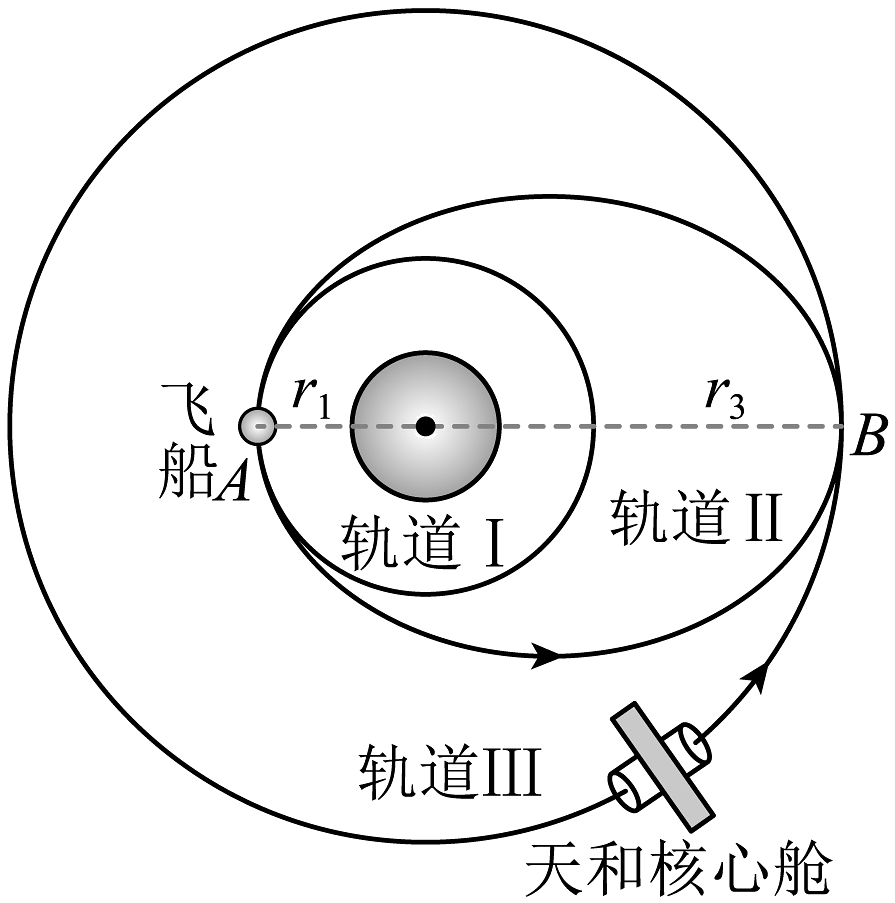 A、由轨道Ⅱ变轨到轨道Ⅲ,需在B处减速 B、在B处与核心舱对接前后的加速度相等 C、在轨道Ⅰ上A处的速度小于在轨道Ⅲ上B处的速度 D、在轨道Ⅱ上由A到B的时间大于在轨道Ⅲ上运行周期的一半5. 如图所示,火星与地球可视为在同一平面内沿同一方向绕太阳做匀速圆周运动。已知地球的公转周期为T,火星轨道半径是地球轨道半径的k倍。地球从a运行到b、火星从c运行到d的过程中,与太阳连线扫过的面积分别为和。下列说法正确的是( )
A、由轨道Ⅱ变轨到轨道Ⅲ,需在B处减速 B、在B处与核心舱对接前后的加速度相等 C、在轨道Ⅰ上A处的速度小于在轨道Ⅲ上B处的速度 D、在轨道Ⅱ上由A到B的时间大于在轨道Ⅲ上运行周期的一半5. 如图所示,火星与地球可视为在同一平面内沿同一方向绕太阳做匀速圆周运动。已知地球的公转周期为T,火星轨道半径是地球轨道半径的k倍。地球从a运行到b、火星从c运行到d的过程中,与太阳连线扫过的面积分别为和。下列说法正确的是( ) A、若小于 , 则可以判定从a运行到b的时间小于从c运行到d的时间 B、火星与地球做圆周运动的向心力大小之比为 C、火星与地球做圆周运动的角速度之比为 D、火星的公转周期为kT6. 2024年 3月 20日,我国探月工程四期鹊桥二号中继星成功发射升空。当抵达距离月球表面某高度时,鹊桥二号开始进行近月制动,并顺利进入捕获轨道运行,如图所示,轨道的半长轴约为 51900km。后经多次轨道调整,进入冻结轨道运行,轨道的半长轴约为 9900km,周期约为 24h。则鹊桥二号在捕获轨道运行时( )
A、若小于 , 则可以判定从a运行到b的时间小于从c运行到d的时间 B、火星与地球做圆周运动的向心力大小之比为 C、火星与地球做圆周运动的角速度之比为 D、火星的公转周期为kT6. 2024年 3月 20日,我国探月工程四期鹊桥二号中继星成功发射升空。当抵达距离月球表面某高度时,鹊桥二号开始进行近月制动,并顺利进入捕获轨道运行,如图所示,轨道的半长轴约为 51900km。后经多次轨道调整,进入冻结轨道运行,轨道的半长轴约为 9900km,周期约为 24h。则鹊桥二号在捕获轨道运行时( ) A、周期约为 144h B、近月点的速度大于远月点的速度 C、近月点的速度小于在冻结轨道运行时近月点的速度 D、近月点的加速度大于在冻结轨道运行时近月点的加速度7. 美国航天局与欧洲航天局合作,发射的火星探测器已经成功登录火星。荷兰企业家巴斯兰斯多普发起的“火星一号”计划打算将总共24人送上火星,创建一块长期殖民地。若已知万有引力常量G,那么在下列给出的各种情景中,能根据测量的数据求出火星密度的是 ( )A、在火星表面使一个小球做自由落体运动,测出落下的高度H和时间t、T B、火星探测器贴近火星表面做匀速圆周运动,测出运行周期T C、火里探测器在高空绕火星做匀速圆周运动,测出距火星表面的高度h和运行周期T D、观察火星绕太阳的匀速圆周运动,测出火星的直径D和运行周期T8. “金星凌日”时,从地球上看,金星就像镶嵌在太阳表面的小黑点。在地球上间距为d的两点同时观测,测得金星在太阳表面的小黑点相距为L,如图所示。地球和金星绕太阳的运动均视为匀速圆周运动,太阳直径远小于金星的轨道半径,则地球和金星绕太阳运动的( )
A、周期约为 144h B、近月点的速度大于远月点的速度 C、近月点的速度小于在冻结轨道运行时近月点的速度 D、近月点的加速度大于在冻结轨道运行时近月点的加速度7. 美国航天局与欧洲航天局合作,发射的火星探测器已经成功登录火星。荷兰企业家巴斯兰斯多普发起的“火星一号”计划打算将总共24人送上火星,创建一块长期殖民地。若已知万有引力常量G,那么在下列给出的各种情景中,能根据测量的数据求出火星密度的是 ( )A、在火星表面使一个小球做自由落体运动,测出落下的高度H和时间t、T B、火星探测器贴近火星表面做匀速圆周运动,测出运行周期T C、火里探测器在高空绕火星做匀速圆周运动,测出距火星表面的高度h和运行周期T D、观察火星绕太阳的匀速圆周运动,测出火星的直径D和运行周期T8. “金星凌日”时,从地球上看,金星就像镶嵌在太阳表面的小黑点。在地球上间距为d的两点同时观测,测得金星在太阳表面的小黑点相距为L,如图所示。地球和金星绕太阳的运动均视为匀速圆周运动,太阳直径远小于金星的轨道半径,则地球和金星绕太阳运动的( )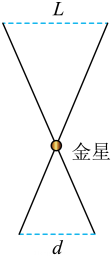 A、轨道半径之比为 B、周期之比为 C、线速度大小之比为 D、向心加速度大小之比为9. 2024年6月,嫦娥六号探测器首次实现月球背面采样返回。如图所示,探测器在圆形轨道1上绕月球飞行,在A点变轨后进入椭圆轨道、为远月点。关于嫦娥六号探测器,下列说法正确的是( )
A、轨道半径之比为 B、周期之比为 C、线速度大小之比为 D、向心加速度大小之比为9. 2024年6月,嫦娥六号探测器首次实现月球背面采样返回。如图所示,探测器在圆形轨道1上绕月球飞行,在A点变轨后进入椭圆轨道、为远月点。关于嫦娥六号探测器,下列说法正确的是( ) A、在轨道2上从A向B运动过程中动能逐渐减小 B、在轨道2上从A向B运动过程中加速度逐渐变大 C、在轨道2上机械能与在轨道1上相等 D、利用引力常量和轨道1的周期,可求出月球的质量10. 地质勘探人员利用重力加速度反常(如地面下方有重金属矿时,重力加速度值比正常值大)可探测地面下的物质分布情况。在地面下某处(远小于地球半径)有一区域内有一重金属矿,探测人员从地面上O点出发,沿水平地面上相互垂直的x、y轴两个方向,测量不同位置的重力加速度值,得到重力加速度值随位置变化如图甲、乙所示,图像的峰值坐标为别为和。由此可初步判断( )
A、在轨道2上从A向B运动过程中动能逐渐减小 B、在轨道2上从A向B运动过程中加速度逐渐变大 C、在轨道2上机械能与在轨道1上相等 D、利用引力常量和轨道1的周期,可求出月球的质量10. 地质勘探人员利用重力加速度反常(如地面下方有重金属矿时,重力加速度值比正常值大)可探测地面下的物质分布情况。在地面下某处(远小于地球半径)有一区域内有一重金属矿,探测人员从地面上O点出发,沿水平地面上相互垂直的x、y轴两个方向,测量不同位置的重力加速度值,得到重力加速度值随位置变化如图甲、乙所示,图像的峰值坐标为别为和。由此可初步判断( ) A、重金属矿的地面位置坐标约为 , 且图像中 B、重金属矿的地面位置坐标约为 , 且图像中 C、重金属矿的地面位置坐标约为 , 且图像中 D、重金属矿的地面位置坐标约为 , 且图像中11. 太阳系曾经上演过“七星连珠”罕见天象。如果行星的运动看作匀速圆周运动,则在运动过程中,距离太阳越远的星球( )
A、重金属矿的地面位置坐标约为 , 且图像中 B、重金属矿的地面位置坐标约为 , 且图像中 C、重金属矿的地面位置坐标约为 , 且图像中 D、重金属矿的地面位置坐标约为 , 且图像中11. 太阳系曾经上演过“七星连珠”罕见天象。如果行星的运动看作匀速圆周运动,则在运动过程中,距离太阳越远的星球( ) A、向心加速度越大 B、线速度越大 C、周期越大 D、角速度越大12. 将于近期择机发射的“天问二号”探测器计划对小行星2016HO3进行伴飞、采样并返回。2016HO3是一颗直径约40-100米的近地小行星,距离地球最近约1400万公里,最远约4000多万公里,因其运行周期与地球高度同步,被称为“地球准卫星”。如图所示,地球绕太阳公转可视作圆轨道,小行星2016HO3绕太阳运行轨道为椭圆,它的近日点位于地球圆轨道内侧。下列说法正确的是( )
A、向心加速度越大 B、线速度越大 C、周期越大 D、角速度越大12. 将于近期择机发射的“天问二号”探测器计划对小行星2016HO3进行伴飞、采样并返回。2016HO3是一颗直径约40-100米的近地小行星,距离地球最近约1400万公里,最远约4000多万公里,因其运行周期与地球高度同步,被称为“地球准卫星”。如图所示,地球绕太阳公转可视作圆轨道,小行星2016HO3绕太阳运行轨道为椭圆,它的近日点位于地球圆轨道内侧。下列说法正确的是( )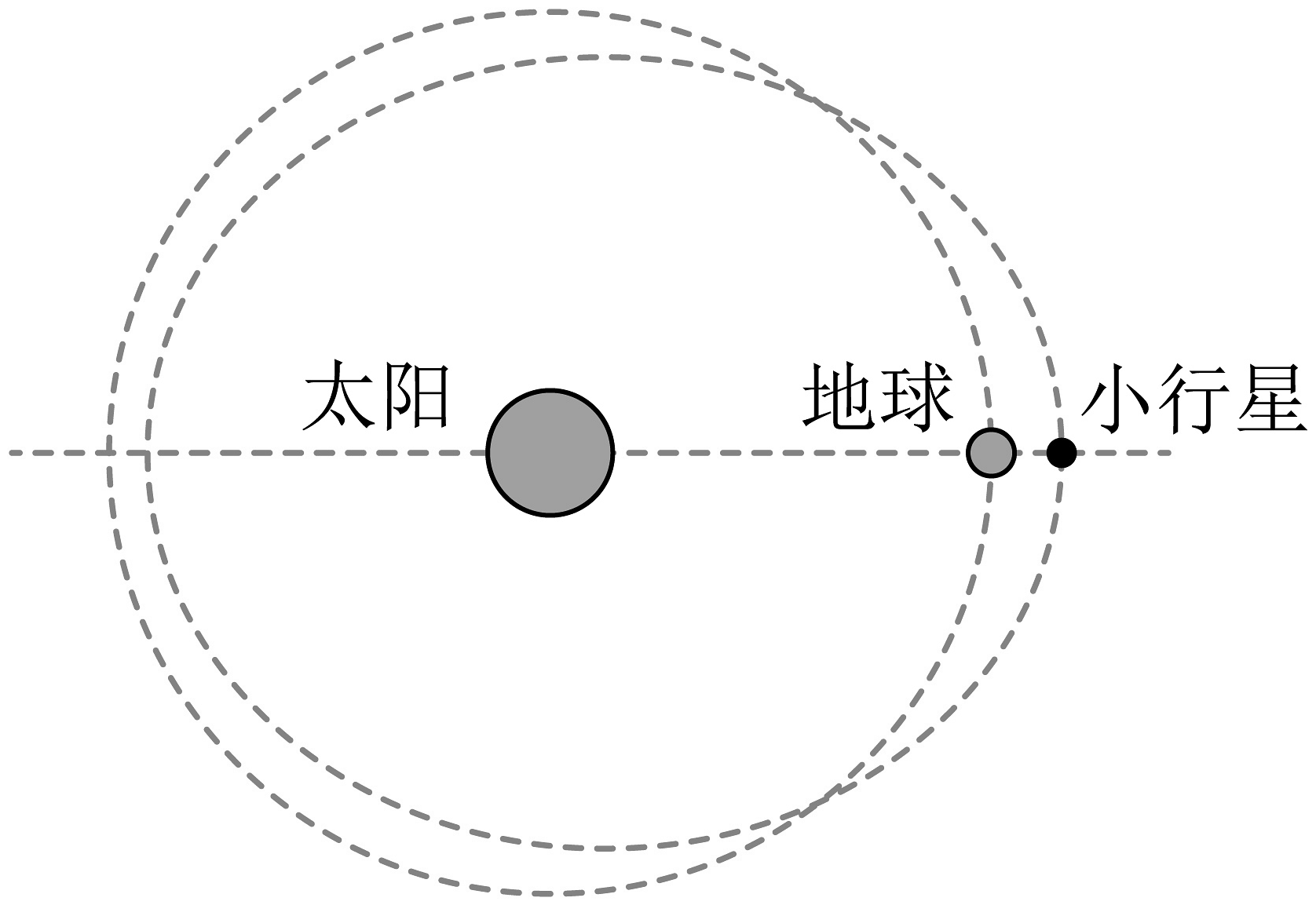 A、探测器的发射速度大于第三宇宙速度 B、探测器在采样时能实时接收地面控制中心的指令 C、小行星在近日点的速度大于地球做圆周运动的速度 D、小行星在远离太阳过程中引力做负功,机械能不断减小13. 我国研制的“天问二号”探测器,任务是对伴地小行星及彗星交会等进行多目标探测。某同学提出探究方案,通过释放卫星绕小行星进行圆周运动,可测得小行星半径R和质量M。为探测某自转周期为的小行星,卫星先在其同步轨道上运行,测得距离小行星表面高度为h,接下来变轨到小行星表面附近绕其做匀速圆周运动,测得周期为。已知引力常量为G,不考虑其他天体对卫星的引力,可根据以上物理得到。下列选项正确的是( )A、a为为为 B、a为为为 C、a为为为 D、a为为为14. 某星球的半径为R,质量为M,若该星球使用四颗静止轨道卫星(同步卫星)恰好能实现该星球的赤道上任意两点的通信。已知引力常量为G,则该星球的自转周期为( )A、 B、 C、 D、15. 所谓“双星”就是两颗相距较近的恒星,这两颗星在彼此之间万有引力作用下,各自以一定的速率始终绕它们连线上的某点转动,则( )A、两颗星做圆周运动的半径之比等于它们质量之比 B、两颗星速度大小之比等于它们质量的反比 C、两颗星的动能之比等于它们做圆周运动的半径的反比 D、两颗星的动量始终相同16. “食双星”是特殊的双星系统,由两颗亮度不同的恒星组成,它们在相互引力作用下绕连线上某点做匀速圆周运动,且轨道平面与观测者视线方向几乎平行。由于两颗恒星相互遮挡,造成观测者观察到双星的亮度L发生周期性变化,如图所示。若较亮的恒星和较暗的恒星轨道半径分别为和(和远小于该双星系统到观测者的距离)。下列说法正确的是( )
A、探测器的发射速度大于第三宇宙速度 B、探测器在采样时能实时接收地面控制中心的指令 C、小行星在近日点的速度大于地球做圆周运动的速度 D、小行星在远离太阳过程中引力做负功,机械能不断减小13. 我国研制的“天问二号”探测器,任务是对伴地小行星及彗星交会等进行多目标探测。某同学提出探究方案,通过释放卫星绕小行星进行圆周运动,可测得小行星半径R和质量M。为探测某自转周期为的小行星,卫星先在其同步轨道上运行,测得距离小行星表面高度为h,接下来变轨到小行星表面附近绕其做匀速圆周运动,测得周期为。已知引力常量为G,不考虑其他天体对卫星的引力,可根据以上物理得到。下列选项正确的是( )A、a为为为 B、a为为为 C、a为为为 D、a为为为14. 某星球的半径为R,质量为M,若该星球使用四颗静止轨道卫星(同步卫星)恰好能实现该星球的赤道上任意两点的通信。已知引力常量为G,则该星球的自转周期为( )A、 B、 C、 D、15. 所谓“双星”就是两颗相距较近的恒星,这两颗星在彼此之间万有引力作用下,各自以一定的速率始终绕它们连线上的某点转动,则( )A、两颗星做圆周运动的半径之比等于它们质量之比 B、两颗星速度大小之比等于它们质量的反比 C、两颗星的动能之比等于它们做圆周运动的半径的反比 D、两颗星的动量始终相同16. “食双星”是特殊的双星系统,由两颗亮度不同的恒星组成,它们在相互引力作用下绕连线上某点做匀速圆周运动,且轨道平面与观测者视线方向几乎平行。由于两颗恒星相互遮挡,造成观测者观察到双星的亮度L发生周期性变化,如图所示。若较亮的恒星和较暗的恒星轨道半径分别为和(和远小于该双星系统到观测者的距离)。下列说法正确的是( )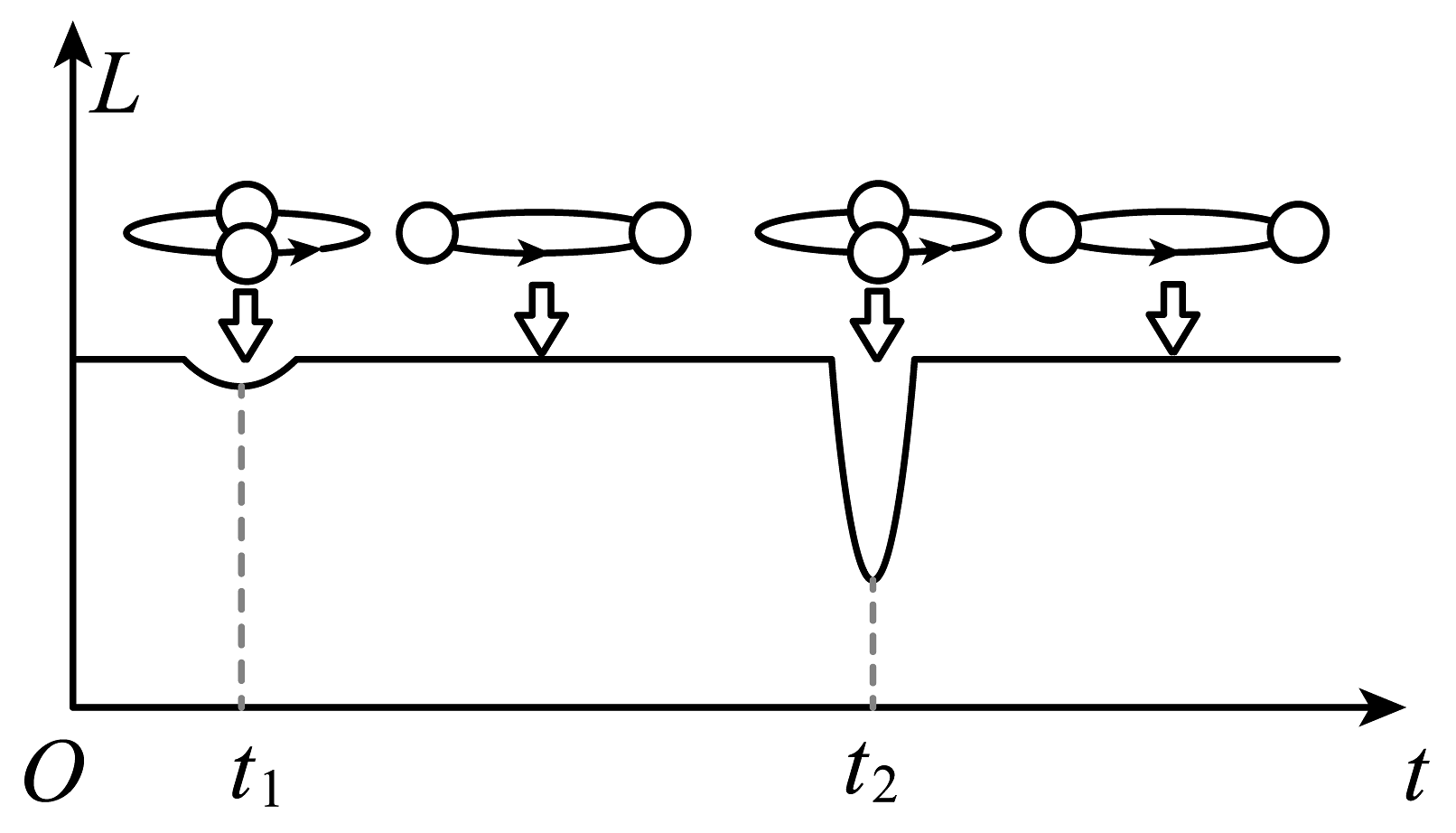 A、时刻,较亮的恒星遮挡住较暗的恒星 B、较亮的恒星与较暗的恒星质量之比为 C、两颗恒星做匀速圆周运动的周期均为 D、较亮的恒星线速度与较暗的恒星线速度之比为17. 宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用,分别围绕其连线上的某一点做周期相同的匀速圆周运动,称之为双星系统.由恒星A与恒星B组成的双星系统绕其连线上的O点做匀速圆周运动,如图所示.已知它们的运行周期为T,恒星A的质量为M,恒星B的质量为3M,引力常量为G,则下列判断正确的是( )
A、时刻,较亮的恒星遮挡住较暗的恒星 B、较亮的恒星与较暗的恒星质量之比为 C、两颗恒星做匀速圆周运动的周期均为 D、较亮的恒星线速度与较暗的恒星线速度之比为17. 宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用,分别围绕其连线上的某一点做周期相同的匀速圆周运动,称之为双星系统.由恒星A与恒星B组成的双星系统绕其连线上的O点做匀速圆周运动,如图所示.已知它们的运行周期为T,恒星A的质量为M,恒星B的质量为3M,引力常量为G,则下列判断正确的是( ) A、两颗恒星相距 B、恒星A与恒星B的向心力之比为3︰1 C、恒星A与恒星B的线速度之比为1︰3 D、恒星A与恒星B的轨道半径之比为︰1
A、两颗恒星相距 B、恒星A与恒星B的向心力之比为3︰1 C、恒星A与恒星B的线速度之比为1︰3 D、恒星A与恒星B的轨道半径之比为︰1二、多项选择题
-
18. 2025年4月,我国已成功构建国际首个基于DRO(远距离逆行轨道)的地月空间三星星座,DRO具有“低能进入、稳定停泊、机动转移”的特点。若卫星甲从DRO变轨进入环月椭圆轨道,该轨道的近月点和远月点距月球表面的高度分别为a和b,卫星的运行周期为T;卫星乙从DRO变轨进入半径为r的环月圆形轨道,周期也为T。月球的质量为M,半径为R,引力常量为G。假设只考虑月球对甲、乙的引力,则( )A、 B、 C、 D、19. 2024 年 5 月 3 日,“嫦娥六号”探测器顺利进入地月转移轨道,正式开启月球之旅。相较于“嫦娥四号”和“嫦娥五号”,本次的主要任务是登陆月球背面进行月壤采集并通过升空器将月壤转移至绕月运行的返回舱,返回舱再通过返回轨道返回地球。设返回舱绕月运行的轨道为圆轨道,半径近似为月球半径。已知月球表面重力加速度约为地球表面的 , 月球半径约为地球半径的。关于返回舱在该绕月轨道上的运动,下列说法正确的是( )A、其相对于月球的速度大于地球第一宇宙速度 B、其相对于月球的速度小于地球第一宇宙速度 C、其绕月飞行周期约为地球上近地圆轨道卫星周期的倍 D、其绕月飞行周期约为地球上近地圆轨道卫星周期的倍20. 2024年3月0日,鹊桥二号中继星成功发射升空,为嫦娥六号在月球背面的探月任务提供地月间中继通讯。鹊桥二号采用周期为24h的环月椭圆冻结轨道(如图),近月点A距月心约为 , 远月点B距月心约为 , CD为椭圆轨道的短轴,下列说法正确的是( )
 A、鹊桥二号从C经B到D的运动时间为12h B、鹊桥二号在两点的加速度大小之比约为81:1 C、鹊桥二号在两点的速度方向垂直于其与月心的连线 D、鹊桥二号在地球表面附近的发射速度大于7.9km/s且小于11.2km/s21. 如图所示,火星与地球可视为在同一平面内沿同一方向绕太阳做匀速圆周运动。已知地球的公转周期为T,火星轨道半径是地球轨道半径的k倍。当火星、地球、太阳三者在同一直线上且地球位于太阳和火星之间时,称为火星冲日。不考虑火星与地球之间的引力,下列说法正确的是( )
A、鹊桥二号从C经B到D的运动时间为12h B、鹊桥二号在两点的加速度大小之比约为81:1 C、鹊桥二号在两点的速度方向垂直于其与月心的连线 D、鹊桥二号在地球表面附近的发射速度大于7.9km/s且小于11.2km/s21. 如图所示,火星与地球可视为在同一平面内沿同一方向绕太阳做匀速圆周运动。已知地球的公转周期为T,火星轨道半径是地球轨道半径的k倍。当火星、地球、太阳三者在同一直线上且地球位于太阳和火星之间时,称为火星冲日。不考虑火星与地球之间的引力,下列说法正确的是( )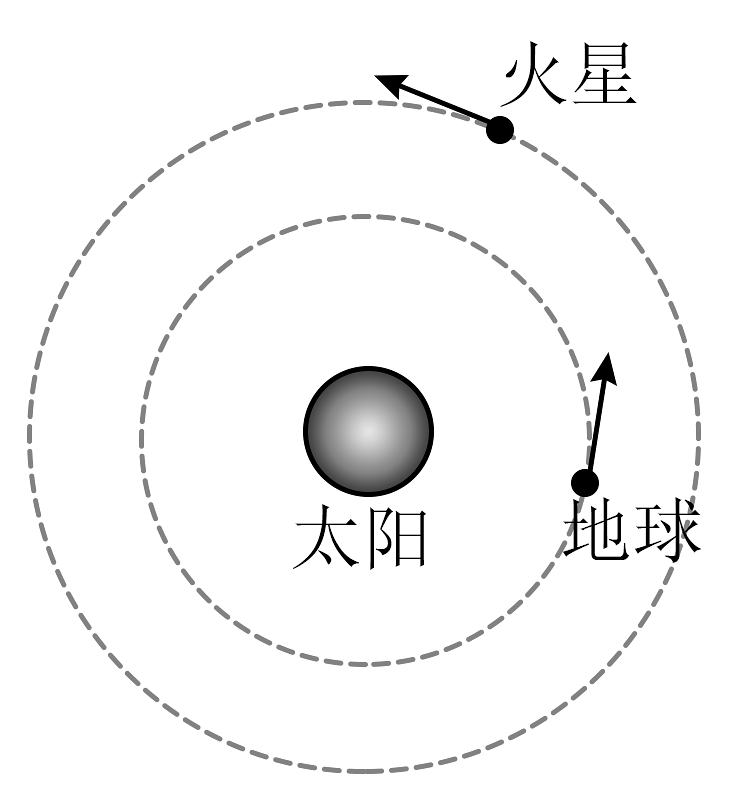 A、火星与地球做圆周运动的向心力大小之比为 B、火星与地球做圆周运动的向心加速度大小之比为 C、火星与地球做圆周运动的角速度之比为 D、相邻两次火星冲日的时间间隔为22. “双星系统”是指在相互间万有引力的作用下,绕连线上某点做匀速圆周运动的两个孤立星球组成的系统。假设在太空中有星球A、B组成的双星系统绕点做顺时针匀速圆周运动,如图所示,两星球的间距为 , 公转周期为。为探索该双星系统,向星球B发射一颗人造卫星C,C绕B运行的周期为 , 轨道半径为 , 忽略C的引力对双星系统的影响,万有引力常量为。则以下说法正确的是( )
A、火星与地球做圆周运动的向心力大小之比为 B、火星与地球做圆周运动的向心加速度大小之比为 C、火星与地球做圆周运动的角速度之比为 D、相邻两次火星冲日的时间间隔为22. “双星系统”是指在相互间万有引力的作用下,绕连线上某点做匀速圆周运动的两个孤立星球组成的系统。假设在太空中有星球A、B组成的双星系统绕点做顺时针匀速圆周运动,如图所示,两星球的间距为 , 公转周期为。为探索该双星系统,向星球B发射一颗人造卫星C,C绕B运行的周期为 , 轨道半径为 , 忽略C的引力对双星系统的影响,万有引力常量为。则以下说法正确的是( ) A、星球A、B的质量之和为 B、星球A做圆周运动的半径为 C、星球B做圆周运动的半径为 D、若A也有一颗周期为的卫星,则其轨道半径一定大于23. 如图所示, 探测器及其保护背罩通过弹性轻绳连接降落伞. 在 接近某行星表面时以 的 速度竖直匀速下落. 此时启动 “背罩分离”, 探测器与背罩断 开连接, 背罩与降落伞保持连接. 已知探测器质量 为 ,背罩质量为 ,该行星的质量和 半径分别为地球的 和 . 地球表面重力加速度大小取 . 忽略大气对探测器和背罩的阻力. 下列说法正确的有 ( )
A、星球A、B的质量之和为 B、星球A做圆周运动的半径为 C、星球B做圆周运动的半径为 D、若A也有一颗周期为的卫星,则其轨道半径一定大于23. 如图所示, 探测器及其保护背罩通过弹性轻绳连接降落伞. 在 接近某行星表面时以 的 速度竖直匀速下落. 此时启动 “背罩分离”, 探测器与背罩断 开连接, 背罩与降落伞保持连接. 已知探测器质量 为 ,背罩质量为 ,该行星的质量和 半径分别为地球的 和 . 地球表面重力加速度大小取 . 忽略大气对探测器和背罩的阻力. 下列说法正确的有 ( ) A、该行星表面的重力加速度大小为 B、该行星的第一宇宙速度为 C、“背罩分离”后瞬间,背罩的加速度大小为 D、“背罩分离”后瞬间, 探测器所受重力对其做功 的功率为
A、该行星表面的重力加速度大小为 B、该行星的第一宇宙速度为 C、“背罩分离”后瞬间,背罩的加速度大小为 D、“背罩分离”后瞬间, 探测器所受重力对其做功 的功率为三、非选择题
-
24. 沿椭圆轨道的运动
行星在椭圆轨道绕日运行,卫星在椭圆轨道绕地运动,生活中也有类似的椭圆轨道运动,有时可将其视作圆周运动进行研究。
(1)、若将太阳系行星轨道近似视作圆,轨道平均半径为R和绕日公转周期为T,下列关于常用对数lgR与lgT的关系图像正确的是( )A、 B、
B、 C、
C、 D、
D、 (2)、卫星绕地球运行的椭圆轨道如图,a、b、c、d为轨道上四点,b是a、d的中间位置,c是b、d的中间位置。则卫星( )
(2)、卫星绕地球运行的椭圆轨道如图,a、b、c、d为轨道上四点,b是a、d的中间位置,c是b、d的中间位置。则卫星( ) A、在a的速度等于在d的速度 B、从b运动到c的时间等于从c运动到d的时间 C、从c运动到d的过程,引力做负功 D、从b运动到c的过程,引力势能减小(3)、用国际单位制中的基本单位表示万有引力常量G的单位,为。(4)、北斗卫星绕地球做高速椭圆轨道运动,只考虑地球引力场的广义相对论效应,星载原子钟比地面接收钟走时更。(选涂“A.快”或“B.慢”)(5)、如图(a),场地自行车的赛车场为椭圆盆形,图(b)是将最内侧弯道视作坡度为30°斜坡的简化图。某时刻运动员在最内侧弯道的骑行速度为20m/s,转弯半径为54m,运动员和自行车整体( )
A、在a的速度等于在d的速度 B、从b运动到c的时间等于从c运动到d的时间 C、从c运动到d的过程,引力做负功 D、从b运动到c的过程,引力势能减小(3)、用国际单位制中的基本单位表示万有引力常量G的单位,为。(4)、北斗卫星绕地球做高速椭圆轨道运动,只考虑地球引力场的广义相对论效应,星载原子钟比地面接收钟走时更。(选涂“A.快”或“B.慢”)(5)、如图(a),场地自行车的赛车场为椭圆盆形,图(b)是将最内侧弯道视作坡度为30°斜坡的简化图。某时刻运动员在最内侧弯道的骑行速度为20m/s,转弯半径为54m,运动员和自行车整体( ) A、向心力方向沿水平方向 B、沿坡道方向不受静摩擦力 C、受到沿坡道向上的静摩擦力 D、受到沿坡道向下的静摩擦力25. 在某星球表面上,一根长为L的细线一端固定,另一端拴一质量为m的砝码,使它在水平面内绕圆心O做角速度为的匀速圆周运动,如图所示。已知此时细线与竖直方向的夹角为θ。
A、向心力方向沿水平方向 B、沿坡道方向不受静摩擦力 C、受到沿坡道向上的静摩擦力 D、受到沿坡道向下的静摩擦力25. 在某星球表面上,一根长为L的细线一端固定,另一端拴一质量为m的砝码,使它在水平面内绕圆心O做角速度为的匀速圆周运动,如图所示。已知此时细线与竖直方向的夹角为θ。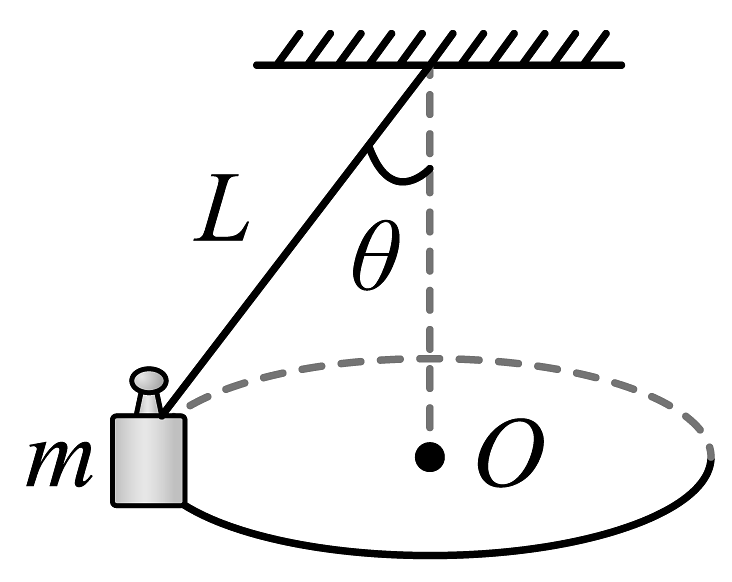 (1)、求该星球表面重力加速度g的大小;(2)、若该星球的半径为R,某卫星在距该星球表面h高处做匀速圆周运动,则该卫星的线速度为多大?(忽略该星球的自转)26. 用如图所示装置探究两个互成角度的力的合成规律。
(1)、求该星球表面重力加速度g的大小;(2)、若该星球的半径为R,某卫星在距该星球表面h高处做匀速圆周运动,则该卫星的线速度为多大?(忽略该星球的自转)26. 用如图所示装置探究两个互成角度的力的合成规律。 (1)、除了弹簧秤、橡皮筋、刻度尺、细绳套之外,以下器材还需选( )A、重锤线 B、量角器 C、三角板(2)、测量完成后,作出力的图示,以两个分力为邻边,做出平行四边形,其对角线(选填“一定”或“不一定”)与橡皮筋共线。(3)、下列各图中,与本实验所用物理思想方法相同的是( )
(1)、除了弹簧秤、橡皮筋、刻度尺、细绳套之外,以下器材还需选( )A、重锤线 B、量角器 C、三角板(2)、测量完成后,作出力的图示,以两个分力为邻边,做出平行四边形,其对角线(选填“一定”或“不一定”)与橡皮筋共线。(3)、下列各图中,与本实验所用物理思想方法相同的是( ) A、甲图:重心概念的提出 B、乙图:伽利略理想斜面实验 C、丙图:探究影响向心力大小的因素 D、丁图:卡文迪许扭秤实验测量万有引力常量27. 如图所示,返回式月球软着陆器在完成了对月球表面的考察任务后,由月球表面回到绕月球做圆周运动的轨道舱。已知月球的半径为R,轨道舱到月球表面的距离为h,引力常量为G,月球表面的重力加速度为g,不考虑月球的自转。求:
A、甲图:重心概念的提出 B、乙图:伽利略理想斜面实验 C、丙图:探究影响向心力大小的因素 D、丁图:卡文迪许扭秤实验测量万有引力常量27. 如图所示,返回式月球软着陆器在完成了对月球表面的考察任务后,由月球表面回到绕月球做圆周运动的轨道舱。已知月球的半径为R,轨道舱到月球表面的距离为h,引力常量为G,月球表面的重力加速度为g,不考虑月球的自转。求: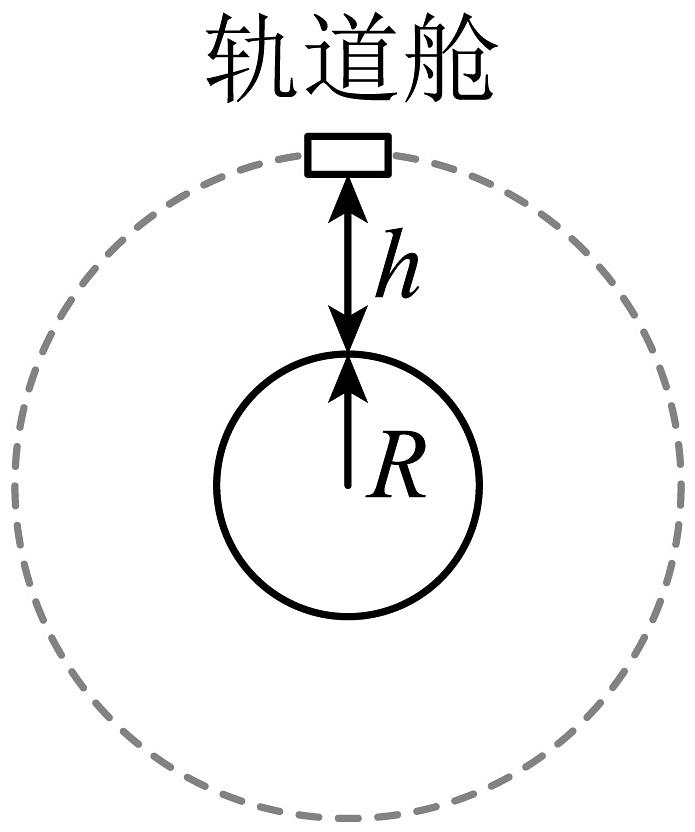 (1)、月球的第一宇宙速度大小;(2)、轨道舱绕月飞行的周期T。28. 某宇航员到达一星球表面,将一质量为m的物体从地面某高度处(高度远小于星球半径)沿水平方向以初速度抛出,经过时间t落地,此时速度方向与水平方向夹角为 , 已知万有引力常量为G,星球的半径R。忽略该星球自转的影响, , 求:
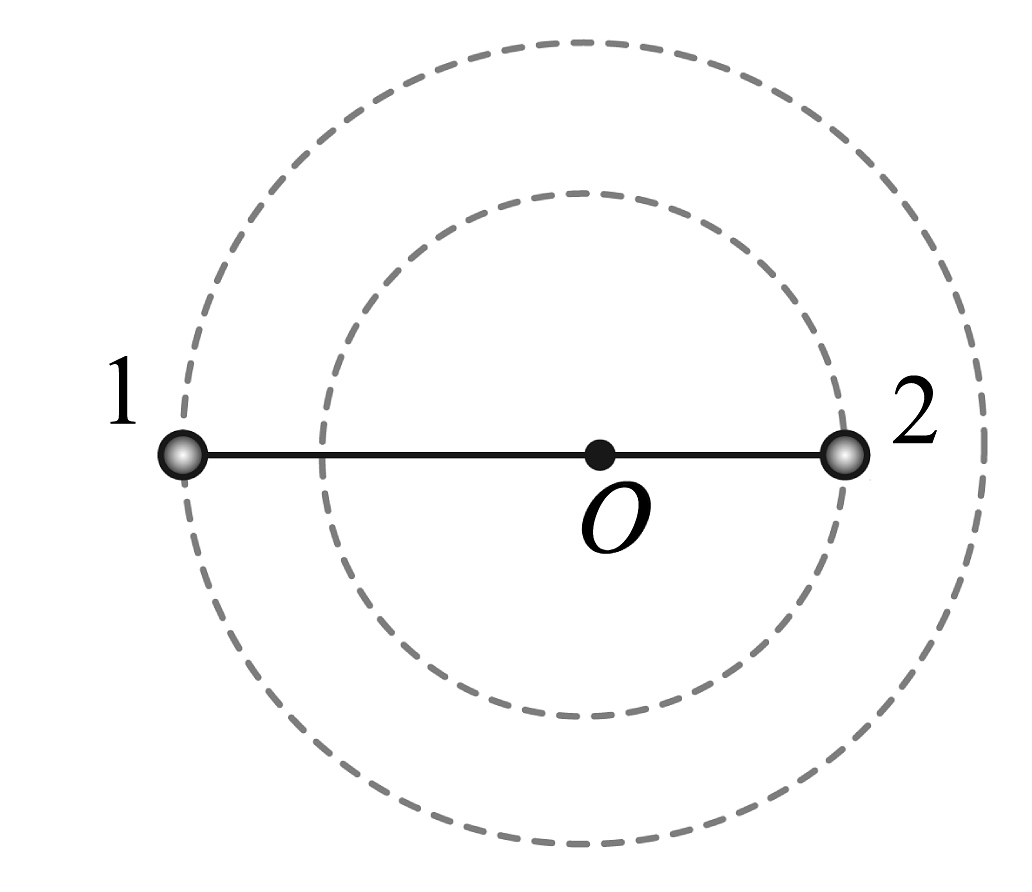
(1)、月球的第一宇宙速度大小;(2)、轨道舱绕月飞行的周期T。28. 某宇航员到达一星球表面,将一质量为m的物体从地面某高度处(高度远小于星球半径)沿水平方向以初速度抛出,经过时间t落地,此时速度方向与水平方向夹角为 , 已知万有引力常量为G,星球的半径R。忽略该星球自转的影响, , 求: (1)、该星球的第一宇宙速度;(2)、该星球的平均密度;(3)、若利用三颗同步卫星全覆盖该星球赤道周围,该星球自转的最小周期。29. 有研究表明,在银河系中至少一半以上的恒星系统都是由双星构成的。由恒星1、2(可视为质点)组成的双星系统如图所示,两恒星以相等的角速度绕两者连线上的O点做圆周运动,测得恒星1、2到O点的距离分别为2r、r,已知恒星1的质量为m,引力常量为G。求:
(1)、该星球的第一宇宙速度;(2)、该星球的平均密度;(3)、若利用三颗同步卫星全覆盖该星球赤道周围,该星球自转的最小周期。29. 有研究表明,在银河系中至少一半以上的恒星系统都是由双星构成的。由恒星1、2(可视为质点)组成的双星系统如图所示,两恒星以相等的角速度绕两者连线上的O点做圆周运动,测得恒星1、2到O点的距离分别为2r、r,已知恒星1的质量为m,引力常量为G。求:(1)恒星2的质量;
(2)恒星1、2间的万有引力大小F;
(3)恒星1的线速度大小。
 30. 回旋加速器是科学家们进行粒子物理研究的重要仪器,将质量的质子在高能粒子加速器中被加速到动能 , 某同学根据算出质子的速度大小v=m/s。此速度值是否合理?(选填“合理”、“不合理”)31. 如图,在平面第一、四象限内存在垂直平面向里的匀强磁场,磁感应强度大小为B,一带正电的粒子从点射入磁场,速度方向与y轴正方向夹角 , 从点射出磁场。已知粒子的电荷量为 , 质量为m,忽略粒子重力及磁场边缘效应。
30. 回旋加速器是科学家们进行粒子物理研究的重要仪器,将质量的质子在高能粒子加速器中被加速到动能 , 某同学根据算出质子的速度大小v=m/s。此速度值是否合理?(选填“合理”、“不合理”)31. 如图,在平面第一、四象限内存在垂直平面向里的匀强磁场,磁感应强度大小为B,一带正电的粒子从点射入磁场,速度方向与y轴正方向夹角 , 从点射出磁场。已知粒子的电荷量为 , 质量为m,忽略粒子重力及磁场边缘效应。 (1)、求粒子射入磁场的速度大小和在磁场中运动的时间。(2)、若在平面内某点固定一负点电荷,电荷量为 , 粒子质量取(k为静电力常量),粒子仍沿(1)中的轨迹从M点运动到N点,求射入磁场的速度大小。(3)、在(2)问条件下,粒子从N点射出磁场开始,经时间速度方向首次与N点速度方向相反,求(电荷量为Q的点电荷产生的电场中,取无限远处的电势为0时,与该点电荷距离为r处的电势)。32. 类比与迁移是物理中常用的思想方法。(1)、对一个周期变化的物理量 , 一个周期内的平均值称为该物理量的“期望”,记为;定义的“标准差”。已知“期望”具有如下性质:。
(1)、求粒子射入磁场的速度大小和在磁场中运动的时间。(2)、若在平面内某点固定一负点电荷,电荷量为 , 粒子质量取(k为静电力常量),粒子仍沿(1)中的轨迹从M点运动到N点,求射入磁场的速度大小。(3)、在(2)问条件下,粒子从N点射出磁场开始,经时间速度方向首次与N点速度方向相反,求(电荷量为Q的点电荷产生的电场中,取无限远处的电势为0时,与该点电荷距离为r处的电势)。32. 类比与迁移是物理中常用的思想方法。(1)、对一个周期变化的物理量 , 一个周期内的平均值称为该物理量的“期望”,记为;定义的“标准差”。已知“期望”具有如下性质:。a.正弦交变电流随时间的变化关系为 , 直接写出其有效值 , 并求出和。
b.说明对任意周期变化的物理量有。
(2)、现有一个质量为m,振动周期为的弹簧振子,不计阻力。a.对于经典物理中的弹簧振子,证明其系统的机械能满足恒等式 , 其中p和x分别是某一相同时刻振子的动量和与平衡位置的距离。
b.在量子力学中,力学系统普遍满足海森堡不确定关系式 , 其中h是普朗克常量。在不确定关系式限制下,该弹簧振子系统的机械能最小值不为0,称为其基态能量。求这一基态能量。提示:除不确定关系式外,其它推导均可以使用经典物理关系式。
33. 类比是研究问题的常用方法。(1)情境1:如图1所示,弹簧振子的平衡位置为O点,在B、C两点之间做简谐运动,小球相对平衡位置的位移x随时间t的变化规律可用方程描述,其中为小球相对平衡位置O时的最大位移,m为小球的质量,k为弹簧的劲度系数。请在图2中画出弹簧的弹力F随位移x变化的示意图,并求出小球从C点到O点的时间。

(2)情境2:假设地球可视为一个质量分布均匀且密度为ρ的球体,地球的半径为R,万有引力常数为G。
a.根据电荷均匀分布的球壳内试探电荷所受库仑力的合力为零,利用库仑力与万有引力的表达式的相似性和相关力学知识,在图3中画出质量为m的小球所受万有引力F与小球到球心之间的距离r的图像,并标出时的纵坐标;

b.若通过地球的南北两极之间能够打通一个真空隧道,把一个质量为m的小球从北极的隧道口(地面处)由静止释放后,小球能够在隧道内运动。求小球从隧道口到地心的时间。
34. 目前我国航天事业正处在飞速发展时期,对于人造卫星的发射,曾经有人提出这样的构想:沿着地球的某条弦挖一通道,并铺设成光滑轨道,在通道的两个出口分别将一物体和待测卫星同时释放,利用两者碰撞(弹性碰撞)效应,就可以将卫星发射出去,已知地表重力加速度 , 地球半径R。物体做简谐运动的周期 , m为物体的质量,为简谐运动物体的回复力和其离开平衡位置的位移大小之比。(1)如图1所示,设想在地球上距地心h处挖一条光滑通道AB,从A点静止释放一个质量为m的物体,求物体通过通道中心的速度大小,以及物体从A运动到B点的时间(质量分布均匀的空腔对空腔内的物体的万有引力为零)
(2)如图2所示,若通道已经挖好,且 , 如果在AB处同时释放两个物体,物体质量分别为M和m,他们同时到达点并发生弹性碰撞,要使小物体飞出通道口速度达到第一宇宙速度,M和m应该满足什么关系?
 35. 2024年4月25日神舟十八号载人飞船成功发射,标志着中国载人航天技术已走在世界前列。有人对今后神舟系列飞船的发射构想:沿着地球的某条弦挖一通道,并铺设成光滑轨道,在通道的两个出口分别将一物体和飞船同时释放,利用两者碰撞(弹性碰撞)效应,将飞船发射出去,已知地表重力加速度g , 地球的半径为R;物体做简谐运动的周期 , m为物体的质量,k为简谐运动物体的回复力和其离开平衡位置的位移大小之比。
35. 2024年4月25日神舟十八号载人飞船成功发射,标志着中国载人航天技术已走在世界前列。有人对今后神舟系列飞船的发射构想:沿着地球的某条弦挖一通道,并铺设成光滑轨道,在通道的两个出口分别将一物体和飞船同时释放,利用两者碰撞(弹性碰撞)效应,将飞船发射出去,已知地表重力加速度g , 地球的半径为R;物体做简谐运动的周期 , m为物体的质量,k为简谐运动物体的回复力和其离开平衡位置的位移大小之比。 (1)、若神州十八号飞船贴近地球表面做匀速圆周运动,则其运行的线速度大小;(2)、如图甲,设想在地球上距地心h处挖一条光滑通道AB , 从A点静止释放一个质量为m的物体,求物体从A运动到B点的时间,以及物体通过通道中心O'的速度大小(质量分布均匀的空腔对空腔内的物体的万有引力为零);(3)、如图乙,若通道已经挖好,且 , 如果在AB处同时释放质量分别为M和m的物体和飞船,他们同时到达O'点并发生弹性碰撞,要使飞船飞出通道口时速度达到第一宇宙速度,M和m应该满足什么关系?36. 某同学甲设想沿地球直径建设一条隧道,封闭后抽成真空,就可以用运输仓在几乎不消耗能量的情况下把物体从地球这的一侧运到另一侧。若地球可看作质量分布均匀的球体,表面重力加速度为g , 半径为R , 隧道大小远小于地球半径,如图甲所示。运输仓从地球表面隧道口A处由静止释放,C为隧道中的一点,且C到地心O的距离为。已知:质量为m的物体做简谐运动的回复力为 , 其周期为;均匀球壳对其内部物体引力为0.求:
(1)、若神州十八号飞船贴近地球表面做匀速圆周运动,则其运行的线速度大小;(2)、如图甲,设想在地球上距地心h处挖一条光滑通道AB , 从A点静止释放一个质量为m的物体,求物体从A运动到B点的时间,以及物体通过通道中心O'的速度大小(质量分布均匀的空腔对空腔内的物体的万有引力为零);(3)、如图乙,若通道已经挖好,且 , 如果在AB处同时释放质量分别为M和m的物体和飞船,他们同时到达O'点并发生弹性碰撞,要使飞船飞出通道口时速度达到第一宇宙速度,M和m应该满足什么关系?36. 某同学甲设想沿地球直径建设一条隧道,封闭后抽成真空,就可以用运输仓在几乎不消耗能量的情况下把物体从地球这的一侧运到另一侧。若地球可看作质量分布均匀的球体,表面重力加速度为g , 半径为R , 隧道大小远小于地球半径,如图甲所示。运输仓从地球表面隧道口A处由静止释放,C为隧道中的一点,且C到地心O的距离为。已知:质量为m的物体做简谐运动的回复力为 , 其周期为;均匀球壳对其内部物体引力为0.求: (1)、运输仓经过C点时的加速度大小a;(2)、运输仓经过C点时的速率及从A第一次到达C所需的时间;(3)、考虑到未来地球表面环境可能会恶化,为了解决人类生存问题,同学乙设想以AC为直径挖出一个球形空腔(如图乙所示),建立一个超级地下城。将一物体从A由静止释放,求物体运动到C的速率及所需的时间各为多少?
(1)、运输仓经过C点时的加速度大小a;(2)、运输仓经过C点时的速率及从A第一次到达C所需的时间;(3)、考虑到未来地球表面环境可能会恶化,为了解决人类生存问题,同学乙设想以AC为直径挖出一个球形空腔(如图乙所示),建立一个超级地下城。将一物体从A由静止释放,求物体运动到C的速率及所需的时间各为多少?