高考一轮复习:曲线运动
试卷更新日期:2025-08-24 类型:一轮复习
一、选择题
-
1. 图为“玉兔二号”巡视器在月球上从O处行走到B处的照片,轨迹OA段是直线,AB段是曲线,巡视器质量为135kg,则巡视器( )
 A、受到月球的引力为1350N B、在AB段运动时一定有加速度 C、OA段与AB段的平均速度方向相同 D、从O到B的位移大小等于OAB轨迹长度2. 物理来源于生活,也可以解释生活。如图所示生活中经常出现的情况,分析正确的是( )
A、受到月球的引力为1350N B、在AB段运动时一定有加速度 C、OA段与AB段的平均速度方向相同 D、从O到B的位移大小等于OAB轨迹长度2. 物理来源于生活,也可以解释生活。如图所示生活中经常出现的情况,分析正确的是( )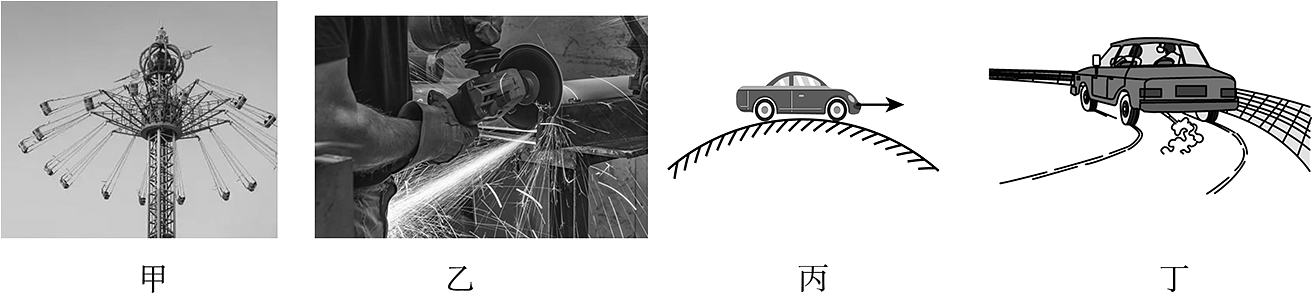 A、图甲中人和飞椅在水平面内做匀速圆周运动时,人的速度保持不变 B、图乙中砂轮打磨下来的炽热微粒离开砂轮时,它的速度方向一定是沿着该处的切线方向的 C、图丙中汽车过拱桥最高点时,速度越大,对桥面的压力越大 D、图丁中若轿车转弯时速度过大发生侧翻,是因为受到的离心力大于向心力3. 如图为小猫蹬地跃起腾空追蝶的情景,则( )
A、图甲中人和飞椅在水平面内做匀速圆周运动时,人的速度保持不变 B、图乙中砂轮打磨下来的炽热微粒离开砂轮时,它的速度方向一定是沿着该处的切线方向的 C、图丙中汽车过拱桥最高点时,速度越大,对桥面的压力越大 D、图丁中若轿车转弯时速度过大发生侧翻,是因为受到的离心力大于向心力3. 如图为小猫蹬地跃起腾空追蝶的情景,则( ) A、飞行的蝴蝶只受重力的作用 B、蝴蝶转弯时所受合力沿运动方向 C、小猫在空中受重力和弹力的作用 D、小猫蹬地时弹力大于所受重力4. 人在距地面高h、离靶面距离L处,将质量m的飞镖以速度v0水平投出,落在靶心正下方,如图所示。只改变h、L、m、v0四个量中的一个,可使飞镖投中靶心的是( )
A、飞行的蝴蝶只受重力的作用 B、蝴蝶转弯时所受合力沿运动方向 C、小猫在空中受重力和弹力的作用 D、小猫蹬地时弹力大于所受重力4. 人在距地面高h、离靶面距离L处,将质量m的飞镖以速度v0水平投出,落在靶心正下方,如图所示。只改变h、L、m、v0四个量中的一个,可使飞镖投中靶心的是( )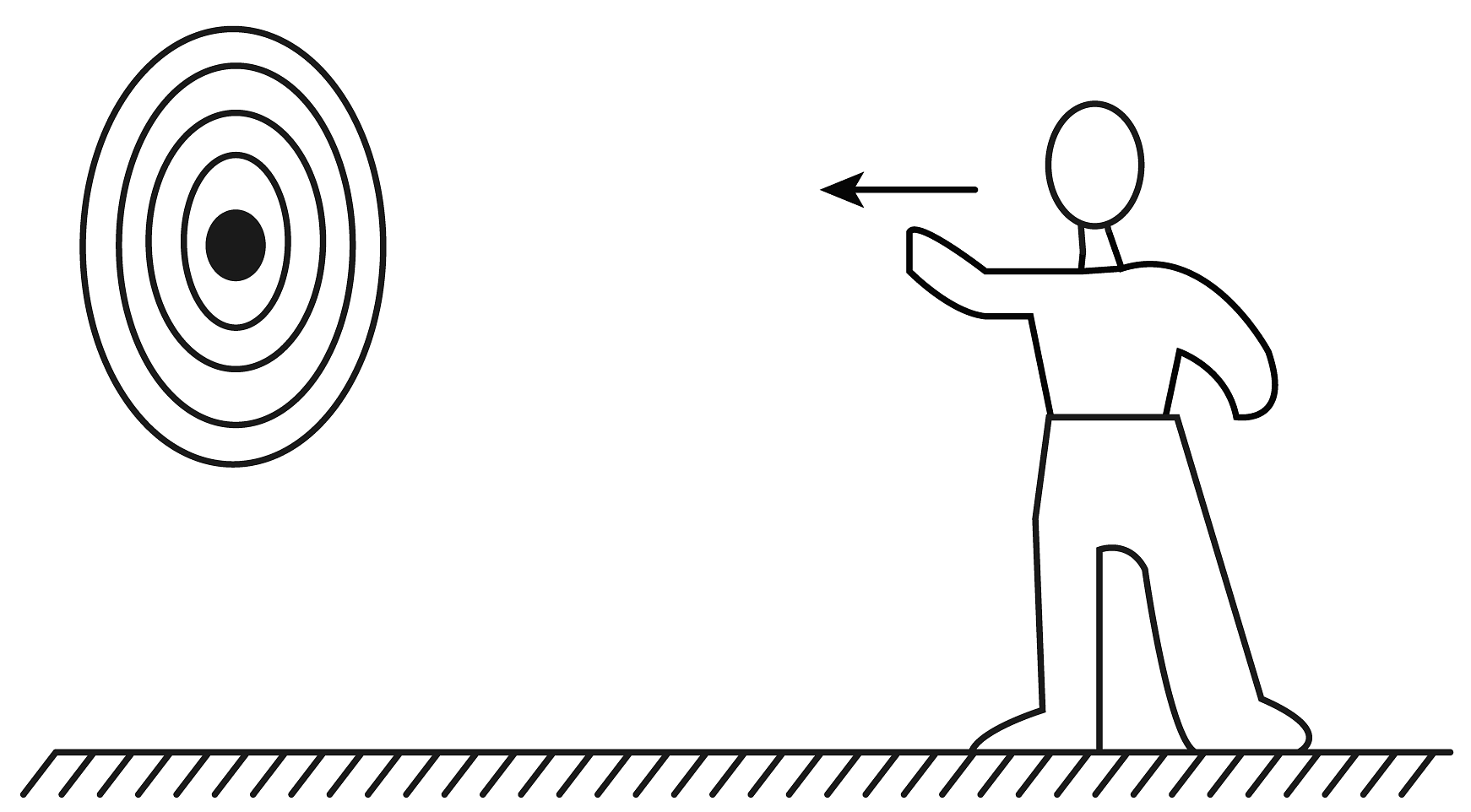 A、适当减小v0 B、适当减小h C、适当减小m D、适当减小L5. 法国科学家皮埃尔·德·费马在1662年提出光线传播的路径是所需时间最少的路径,即费马原理,光的折射即遵从这一原理实际生活中的下述现象也可类比折射定律来理解。如图所示,地面上陶陶在距笔直的河岸10m处的A点,发现落水的琪琪位于水面上距河岸50m处的B点。陶陶在地面上奔跑的速度大小为 , 在水中游泳的速度大小为 , 奔跑、游泳均视为匀速直线运动。可知此次营救中,陶陶在陆地的速度与河岸夹角30°,在水中的速度与河岸夹角60°将最省时。由题中信息和所学物理知识可知( )
A、适当减小v0 B、适当减小h C、适当减小m D、适当减小L5. 法国科学家皮埃尔·德·费马在1662年提出光线传播的路径是所需时间最少的路径,即费马原理,光的折射即遵从这一原理实际生活中的下述现象也可类比折射定律来理解。如图所示,地面上陶陶在距笔直的河岸10m处的A点,发现落水的琪琪位于水面上距河岸50m处的B点。陶陶在地面上奔跑的速度大小为 , 在水中游泳的速度大小为 , 奔跑、游泳均视为匀速直线运动。可知此次营救中,陶陶在陆地的速度与河岸夹角30°,在水中的速度与河岸夹角60°将最省时。由题中信息和所学物理知识可知( )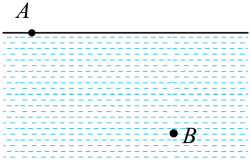 A、陶陶在水中游泳的速度大小为 B、陶陶在水中游泳的速度大小为 C、陶陶到达琪琪处的最短时间为12s D、陶陶到达琪琪处的最短时间约为16s6. 2023年11月29日美国《自然》杂志发表了新发现----“完美太阳系”。星系中的6颗行星大小差不多,以一种和谐的方式围绕一颗恒星a公转。6颗行星依照离恒星由近到远被以英文字母b、c、d、e、f、g编号。星系中的行星存在罕见的轨道共振现象,其中,b、c、d、e这四颗行星存在3比2的轨道共振率,即离恒星较近的行星每公转3圈,紧邻它外侧的行星公转2圈。e、f、g的轨道共振率是4比3。把行星的运动简化为圆周运动,且只受到中央恒星的引力作用。令b行星的运行周期为T,下列选项中正确的为( )
A、陶陶在水中游泳的速度大小为 B、陶陶在水中游泳的速度大小为 C、陶陶到达琪琪处的最短时间为12s D、陶陶到达琪琪处的最短时间约为16s6. 2023年11月29日美国《自然》杂志发表了新发现----“完美太阳系”。星系中的6颗行星大小差不多,以一种和谐的方式围绕一颗恒星a公转。6颗行星依照离恒星由近到远被以英文字母b、c、d、e、f、g编号。星系中的行星存在罕见的轨道共振现象,其中,b、c、d、e这四颗行星存在3比2的轨道共振率,即离恒星较近的行星每公转3圈,紧邻它外侧的行星公转2圈。e、f、g的轨道共振率是4比3。把行星的运动简化为圆周运动,且只受到中央恒星的引力作用。令b行星的运行周期为T,下列选项中正确的为( ) A、行星c与行星e的运行周期之比为9:4 B、a、b、d三个天体每经过时间会重新处于同一直线 C、行星b与行星g的运行轨道半径之比 D、经过时间t(t<T)后b行星与d行星运动划过的面积之比为7. 某物体同时受到在同一平面内的几个恒力作用而平衡,某时刻突然撤去其中一个力,以后这物体将不可能做( )A、平抛运动 B、匀速圆周运动 C、匀加速直线运动 D、匀减速直线运动8. 杂技表演中,为了提高观赏性,摩托车手设计沿如图所示圆锥面的内壁做圆周运动,运动半径为R,(假设摩托车视为质点)则( )
A、行星c与行星e的运行周期之比为9:4 B、a、b、d三个天体每经过时间会重新处于同一直线 C、行星b与行星g的运行轨道半径之比 D、经过时间t(t<T)后b行星与d行星运动划过的面积之比为7. 某物体同时受到在同一平面内的几个恒力作用而平衡,某时刻突然撤去其中一个力,以后这物体将不可能做( )A、平抛运动 B、匀速圆周运动 C、匀加速直线运动 D、匀减速直线运动8. 杂技表演中,为了提高观赏性,摩托车手设计沿如图所示圆锥面的内壁做圆周运动,运动半径为R,(假设摩托车视为质点)则( )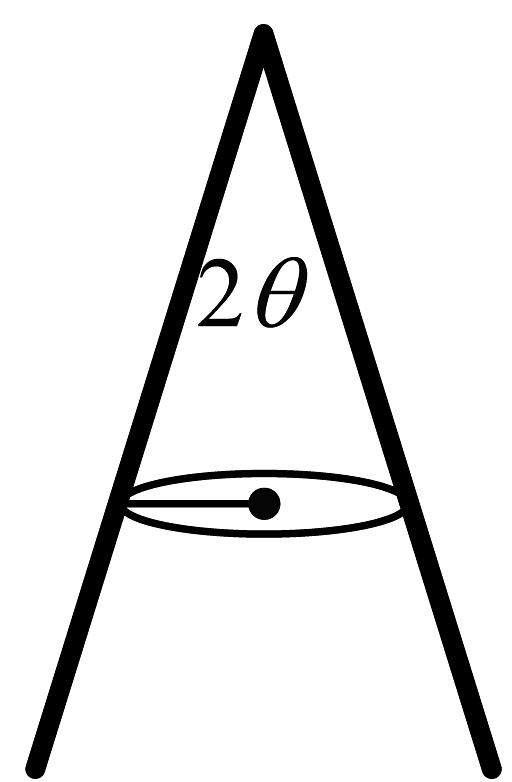 A、摩托车越重越不容易实现圆锥面的内壁做圆周运动 B、摩托车无法实现圆锥面的内壁做圆周运动 C、摩托车做圆周运动的角速度需要满足 D、摩托车做圆周运动时车胎橡胶与圆锥内表面间的动摩擦因数9. 2021年5月15日,天问一号探测器着陆火星取得成功,迈出了我国星际探测征程的重要一步,在火属上首次留下国人的印迹。天问一号探测器成功发射后,顺利被火星捕获,成为我国第一颗人造火星卫星。经过轨道调整,探测器先沿椭圆轨道Ⅰ运行,之后进入称为火星停泊轨道的椭圆轨道Ⅱ运行,如图所示,两轨道相切于近火点P,则天问一号探测器( )
A、摩托车越重越不容易实现圆锥面的内壁做圆周运动 B、摩托车无法实现圆锥面的内壁做圆周运动 C、摩托车做圆周运动的角速度需要满足 D、摩托车做圆周运动时车胎橡胶与圆锥内表面间的动摩擦因数9. 2021年5月15日,天问一号探测器着陆火星取得成功,迈出了我国星际探测征程的重要一步,在火属上首次留下国人的印迹。天问一号探测器成功发射后,顺利被火星捕获,成为我国第一颗人造火星卫星。经过轨道调整,探测器先沿椭圆轨道Ⅰ运行,之后进入称为火星停泊轨道的椭圆轨道Ⅱ运行,如图所示,两轨道相切于近火点P,则天问一号探测器( ) A、在轨道Ⅱ上处于受力平衡状态 B、在轨道Ⅰ运行周期比在Ⅱ时短 C、从轨道Ⅰ进入Ⅱ在P处要加速 D、沿轨道Ⅰ向P飞近时速度增大10. 如图所示,下列有关生活中圆周运动实例分析,其中说法正确的是( )
A、在轨道Ⅱ上处于受力平衡状态 B、在轨道Ⅰ运行周期比在Ⅱ时短 C、从轨道Ⅰ进入Ⅱ在P处要加速 D、沿轨道Ⅰ向P飞近时速度增大10. 如图所示,下列有关生活中圆周运动实例分析,其中说法正确的是( ) A、图1中汽车通过凹形桥的最低点时,汽车处于失重状态 B、图2中旋转秋千装置中,等长绳索对质量相等座椅A、B的拉力相等 C、图3中在铁路转弯处,设计外轨比内轨高,目的是火车转弯时减小轮缘与外轨的侧压力 D、图4中脱水桶原理是水滴受到的离心力大于它受到的向心力,从而沿切线方向甩出11. 如图所示,三个完全相同的半圆形光滑轨道竖直放置,分别处在真空、匀强磁场和匀强电场中,轨道两端在同一高度上。P、M、N分别为轨道的最低点。a、b、c三个相同的带正电绝缘小球同时从轨道左端最高点由静止开始沿轨道运动,则( )
A、图1中汽车通过凹形桥的最低点时,汽车处于失重状态 B、图2中旋转秋千装置中,等长绳索对质量相等座椅A、B的拉力相等 C、图3中在铁路转弯处,设计外轨比内轨高,目的是火车转弯时减小轮缘与外轨的侧压力 D、图4中脱水桶原理是水滴受到的离心力大于它受到的向心力,从而沿切线方向甩出11. 如图所示,三个完全相同的半圆形光滑轨道竖直放置,分别处在真空、匀强磁场和匀强电场中,轨道两端在同一高度上。P、M、N分别为轨道的最低点。a、b、c三个相同的带正电绝缘小球同时从轨道左端最高点由静止开始沿轨道运动,则( )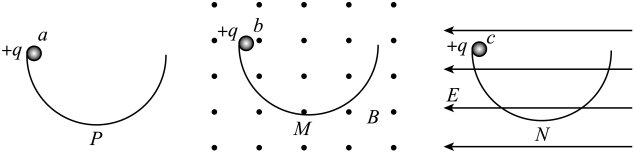 A、b球先于a球到达轨道的最低点 B、a、b两球第一次经过轨道最低点时,b球对轨道的压力更小 C、三小球向下运动过程中,c球到达轨道最低点的速度最小 D、c球运动过程中,其重力势能最小时,电势能一定最大12. 长江路下穿隧道可以理想化为一段R=1km的竖直圆弧,如图所示一辆质量为m=2.5t的小车(可作为质点)经过A时速度vA=10m/s,若该车关闭发动机从A到B滑行且无机械能损失(B为圆弧最低点,g=10 m/s2),则( )
A、b球先于a球到达轨道的最低点 B、a、b两球第一次经过轨道最低点时,b球对轨道的压力更小 C、三小球向下运动过程中,c球到达轨道最低点的速度最小 D、c球运动过程中,其重力势能最小时,电势能一定最大12. 长江路下穿隧道可以理想化为一段R=1km的竖直圆弧,如图所示一辆质量为m=2.5t的小车(可作为质点)经过A时速度vA=10m/s,若该车关闭发动机从A到B滑行且无机械能损失(B为圆弧最低点,g=10 m/s2),则( )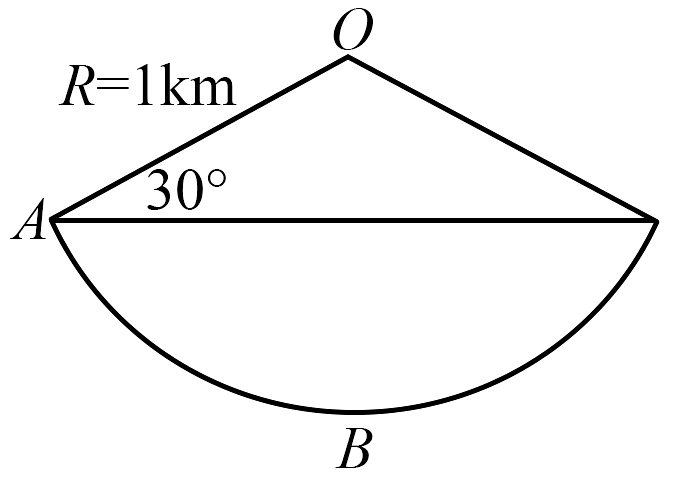 A、车经过A点时,道路的支持力为 B、车经过B点时,道路的支持力为 C、车从A运动到B的过程中,车受到合外力做功为零 D、车经过B点时速度为13. 某同学用不可伸长的细线系一个质量为0.1kg的发光小球,让小球在竖直面内绕一固定点做半径为0.6m的圆周运动,在小球经过最低点附近时拍摄了一张照片,曝光时间为:S.由于小球运动,在照片上留下了一条长度约为半径的圆弧形径迹。根据以上数据估算小球在最低点时细线的拉力大小为A、11N B、9N C、7N D、5N14. 游乐设施“旋转杯”的底盘和转杯分别以、为转轴,在水平面内沿顺时针方向匀速转动。固定在底盘上。某时刻转杯转到如图所示位置,杯上A点与、恰好在同一条直线上。则( )
A、车经过A点时,道路的支持力为 B、车经过B点时,道路的支持力为 C、车从A运动到B的过程中,车受到合外力做功为零 D、车经过B点时速度为13. 某同学用不可伸长的细线系一个质量为0.1kg的发光小球,让小球在竖直面内绕一固定点做半径为0.6m的圆周运动,在小球经过最低点附近时拍摄了一张照片,曝光时间为:S.由于小球运动,在照片上留下了一条长度约为半径的圆弧形径迹。根据以上数据估算小球在最低点时细线的拉力大小为A、11N B、9N C、7N D、5N14. 游乐设施“旋转杯”的底盘和转杯分别以、为转轴,在水平面内沿顺时针方向匀速转动。固定在底盘上。某时刻转杯转到如图所示位置,杯上A点与、恰好在同一条直线上。则( ) A、A点做匀速圆周运动 B、点做匀速圆周运动 C、此时A点的速度小于点 D、此时A点的速度等于点15. 轨道舱与返回舱的组合体,绕质量为M的行星做半径为r的圆周运动,轨道舱与返回舱的质量比为5:1。如图所示,轨道舱在P点沿运动方向向前弹射返回舱,分开瞬间返回舱相对行星的速度大小为2 , G为引力常量,此时轨道舱相对行星的速度大小为
A、A点做匀速圆周运动 B、点做匀速圆周运动 C、此时A点的速度小于点 D、此时A点的速度等于点15. 轨道舱与返回舱的组合体,绕质量为M的行星做半径为r的圆周运动,轨道舱与返回舱的质量比为5:1。如图所示,轨道舱在P点沿运动方向向前弹射返回舱,分开瞬间返回舱相对行星的速度大小为2 , G为引力常量,此时轨道舱相对行星的速度大小为 A、 B、 C、 D、16. 如图所示为嫦娥六号探测器登月的简化过程,探测器从地球表面a点发射至地月转移轨道,在b点被月球捕获后沿椭圆轨道运动,进而在b点变轨后沿近月圆形轨道运动,则探测器( )
A、 B、 C、 D、16. 如图所示为嫦娥六号探测器登月的简化过程,探测器从地球表面a点发射至地月转移轨道,在b点被月球捕获后沿椭圆轨道运动,进而在b点变轨后沿近月圆形轨道运动,则探测器( )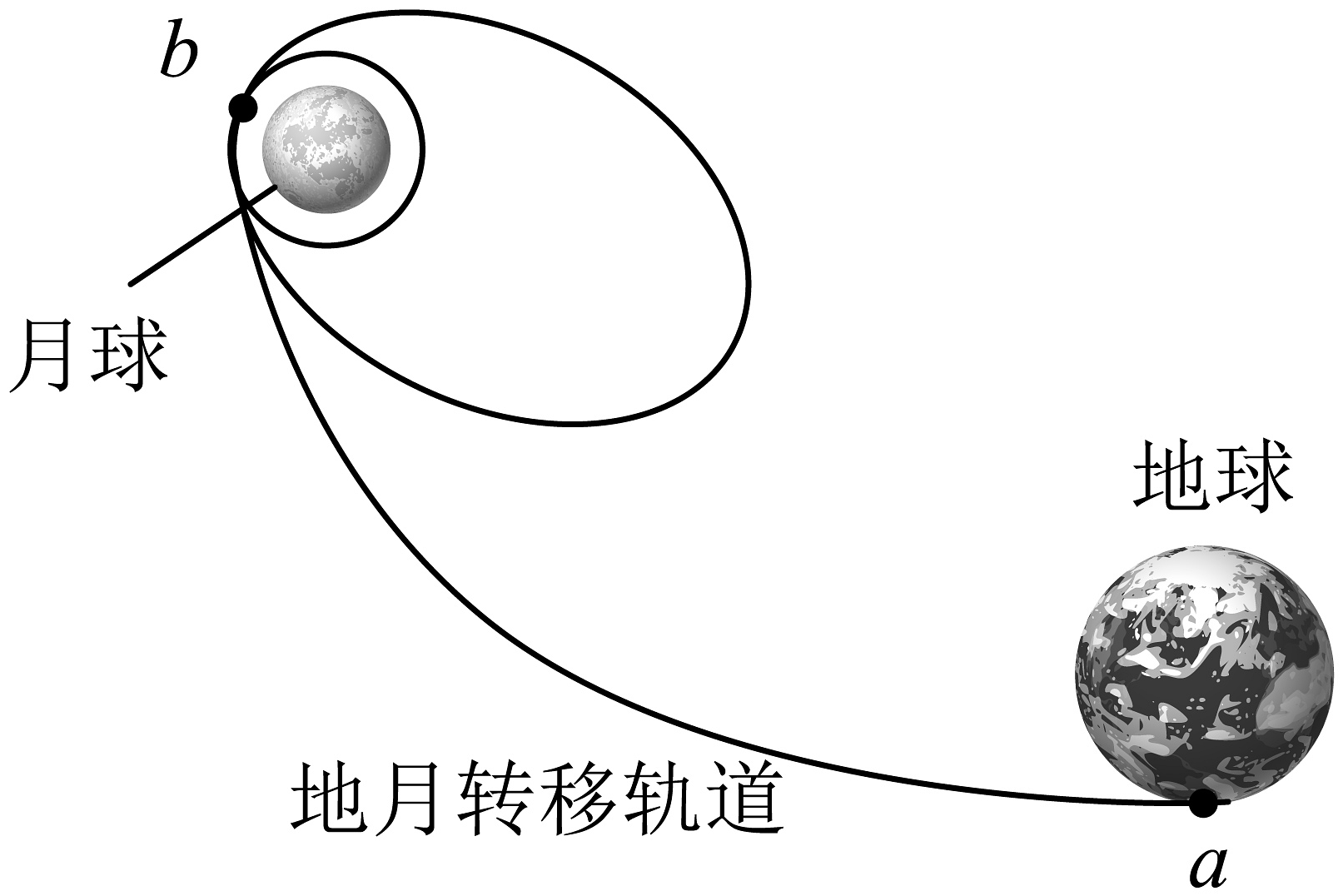 A、探测器被月球捕获后在椭圆轨道上经过b点时应该加速才能进入圆形轨道 B、探测器在椭圆轨道上b点的速度大于月球的第一宇宙速度 C、探测器在地月转移轨道上远离地球时的速度均大于7.9km/s D、探测器在椭圆轨道上的周期小于圆形轨道上的周期17. 如图,新风系统除尘由机械除尘和静电除尘两部分构成,其中静电除尘是通过电离空气后使空气中的粉尘微粒带电,从而被电极吸附的空气净化技术。下图虚线为一带电粉尘(不计重力)在静电除尘管道内的运动轨迹,实线为电场线(未标方向),下列判定正确的是( )
A、探测器被月球捕获后在椭圆轨道上经过b点时应该加速才能进入圆形轨道 B、探测器在椭圆轨道上b点的速度大于月球的第一宇宙速度 C、探测器在地月转移轨道上远离地球时的速度均大于7.9km/s D、探测器在椭圆轨道上的周期小于圆形轨道上的周期17. 如图,新风系统除尘由机械除尘和静电除尘两部分构成,其中静电除尘是通过电离空气后使空气中的粉尘微粒带电,从而被电极吸附的空气净化技术。下图虚线为一带电粉尘(不计重力)在静电除尘管道内的运动轨迹,实线为电场线(未标方向),下列判定正确的是( ) A、带电粉尘带正电 B、带电粉尘在除尘管道内做匀变速曲线运动 C、带电粉尘在a点的加速度小于在b点的加速度 D、带电粉尘在a点的电势能大于在b点的电势能18. 从一倾角θ=30°的斜面顶端抛出一个小球,小球的初速度大小为 , 方向与水平方向成α=45°,在斜面底端放置一足够长的竖直挡板,小球抛出后直接打到挡板,反弹后垂直打在斜面上。重力加速度为g,不计空气阻力,小球与挡板的碰撞为弹性碰撞,即垂直挡板方向的速度大小不变方向反向,竖直方向速度不变,则与挡板碰撞一次后打在斜面上的落点与抛出点的距离是( )
A、带电粉尘带正电 B、带电粉尘在除尘管道内做匀变速曲线运动 C、带电粉尘在a点的加速度小于在b点的加速度 D、带电粉尘在a点的电势能大于在b点的电势能18. 从一倾角θ=30°的斜面顶端抛出一个小球,小球的初速度大小为 , 方向与水平方向成α=45°,在斜面底端放置一足够长的竖直挡板,小球抛出后直接打到挡板,反弹后垂直打在斜面上。重力加速度为g,不计空气阻力,小球与挡板的碰撞为弹性碰撞,即垂直挡板方向的速度大小不变方向反向,竖直方向速度不变,则与挡板碰撞一次后打在斜面上的落点与抛出点的距离是( )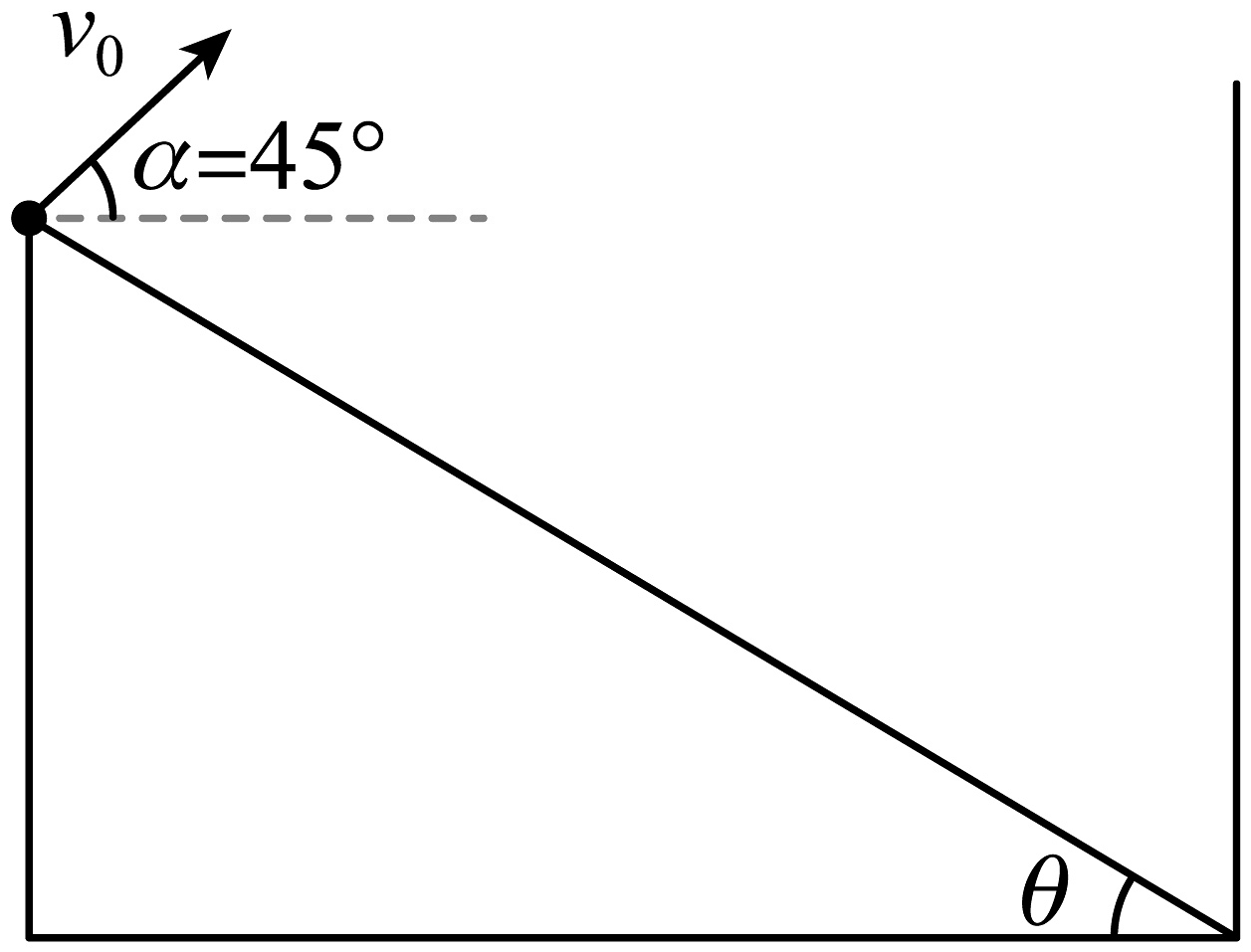 A、 B、 C、 D、19. 如图所示,在水平桌面上有一轻质弹簧,弹簧左端固定,现有一质量为m的小球(可视为质点)将水平轻质弹簧压缩x0长度后由静止释放,小球弹出后经A点水平抛出,恰好从B点沿B点切线方向进入半径为R的竖直圆管中(圆管内径略大于小球直径),小球从圆管最高点E离开后又恰能到达B点。已知E、O、C三点在同一竖直线上,∠BOC=60°,弹簧的弹性势能Ep与弹簧的形变量x以及弹簧的劲度系数k之间的关系式为 , 重力加速度为g,不计空气阻力和所有摩擦,则小球经弹簧弹出从A到达E又回到B的过程中,下列说法正确的是( )
A、 B、 C、 D、19. 如图所示,在水平桌面上有一轻质弹簧,弹簧左端固定,现有一质量为m的小球(可视为质点)将水平轻质弹簧压缩x0长度后由静止释放,小球弹出后经A点水平抛出,恰好从B点沿B点切线方向进入半径为R的竖直圆管中(圆管内径略大于小球直径),小球从圆管最高点E离开后又恰能到达B点。已知E、O、C三点在同一竖直线上,∠BOC=60°,弹簧的弹性势能Ep与弹簧的形变量x以及弹簧的劲度系数k之间的关系式为 , 重力加速度为g,不计空气阻力和所有摩擦,则小球经弹簧弹出从A到达E又回到B的过程中,下列说法正确的是( ) A、小球从圆管最高点E离开时受到圆管壁竖直向下的压力大小为 B、小球从A点水平抛出的速度大小为 C、A、B两点之间的高度差为 D、弹簧的劲度系数为
A、小球从圆管最高点E离开时受到圆管壁竖直向下的压力大小为 B、小球从A点水平抛出的速度大小为 C、A、B两点之间的高度差为 D、弹簧的劲度系数为二、多项选择题
-
20. 将可视为质点的小球沿光滑冰坑内壁推出,使小球在水平面内做匀速圆周运动,如图所示。已知圆周 运动半径R为0.4m,小球所在位置处的切面与水平面夹角θ为45°,小球质量为0.1kg,重力加速度g取10m/s2。关于该小球,下列说法正确的有( )
 A、角速度为5rad/s B、线速度大小为4m/s C、向心加速度大小为10m/s2 D、所受支持力大小为1N21. 如图所示,在无人机的某次定点投放性能测试中,目标区域是水平地面上以O点为圆心,半径R1=5m的圆形区域,OO’垂直地面,无人机在离地面高度H=20m的空中绕O'点、平行地面做半径R2=3m的匀速圆周运动,A、B为圆周上的两点,∠AO'B=90°。若物品相对无人机无初速度地释放,为保证落点在目标区域内,无人机做圆周运动的最大角速度应为为。当无人机以沿圆周运动经过A点时,相对无人机无初速度地释放物品。不计空气对物品运动的影响,物品可视为质点且落地后即静止,重力加速度大小g=10m/s2。下列说法正确的是( )
A、角速度为5rad/s B、线速度大小为4m/s C、向心加速度大小为10m/s2 D、所受支持力大小为1N21. 如图所示,在无人机的某次定点投放性能测试中,目标区域是水平地面上以O点为圆心,半径R1=5m的圆形区域,OO’垂直地面,无人机在离地面高度H=20m的空中绕O'点、平行地面做半径R2=3m的匀速圆周运动,A、B为圆周上的两点,∠AO'B=90°。若物品相对无人机无初速度地释放,为保证落点在目标区域内,无人机做圆周运动的最大角速度应为为。当无人机以沿圆周运动经过A点时,相对无人机无初速度地释放物品。不计空气对物品运动的影响,物品可视为质点且落地后即静止,重力加速度大小g=10m/s2。下列说法正确的是( ) A、 B、 C、无人机运动到B点时,在A点释放的物品已经落地 D、无人机运动到B点时,在4点释放的物品尚未落地22. 春晚上转手绢的机器人,手绢上有P、Q两点,圆心为O, , 手绢做匀速圆周运动,则( )
A、 B、 C、无人机运动到B点时,在A点释放的物品已经落地 D、无人机运动到B点时,在4点释放的物品尚未落地22. 春晚上转手绢的机器人,手绢上有P、Q两点,圆心为O, , 手绢做匀速圆周运动,则( ) A、P、Q线速度之比为 B、P、Q角速度之比为 C、P、Q向心加速度之比为 D、P点所受合外力总是指向O23. 如图所示的虚线为一簇等势线,且相邻两等势线之间的电势差相等,图中的实线为粒子的轨迹(粒子仅受电场力作用),已知粒子质量为m、电荷量为(),粒子经过等势线1时的速度为 , 粒子经过等势线3时的速度为 , 规定等势线1的电势为0。则下列说法正确的是( )
A、P、Q线速度之比为 B、P、Q角速度之比为 C、P、Q向心加速度之比为 D、P点所受合外力总是指向O23. 如图所示的虚线为一簇等势线,且相邻两等势线之间的电势差相等,图中的实线为粒子的轨迹(粒子仅受电场力作用),已知粒子质量为m、电荷量为(),粒子经过等势线1时的速度为 , 粒子经过等势线3时的速度为 , 规定等势线1的电势为0。则下列说法正确的是( )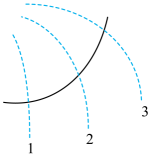 A、粒子经过等势线2时所受电场力方向沿虚线2的切线且指向轨迹凹侧 B、粒子经过等势线2时的速度为 C、等势线2和等势线3之间的电势差 D、粒子经等势线2时的电势能为24. 物理来源于生活,也可以解释生活。对于如图所示生活中经常出现的情况,分析正确的是( )
A、粒子经过等势线2时所受电场力方向沿虚线2的切线且指向轨迹凹侧 B、粒子经过等势线2时的速度为 C、等势线2和等势线3之间的电势差 D、粒子经等势线2时的电势能为24. 物理来源于生活,也可以解释生活。对于如图所示生活中经常出现的情况,分析正确的是( )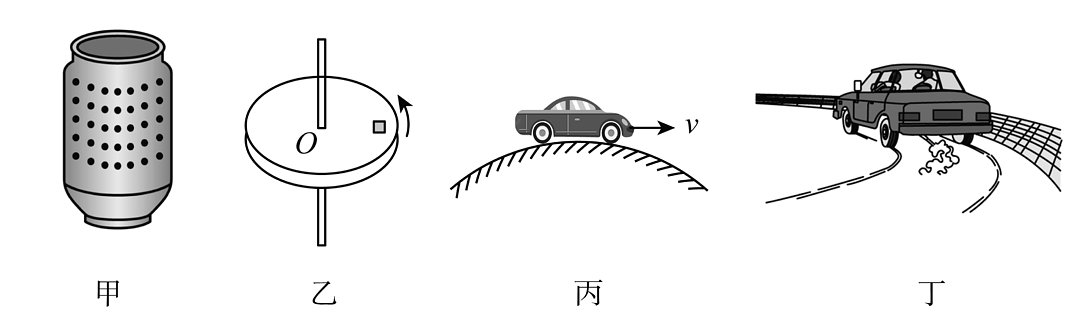 A、图甲所示为洗衣机脱水桶,其脱水原理是利用了超重现象 B、图乙中物体随水平圆盘一起做圆周运动时,只受到指向圆盘圆心的摩擦力 C、图丙中汽车过拱桥最高点时,速度越大,对桥面的压力越小 D、图丁中若轿车转弯时速度过大发生侧翻,是因为需要的向心力大于提供的向心力
A、图甲所示为洗衣机脱水桶,其脱水原理是利用了超重现象 B、图乙中物体随水平圆盘一起做圆周运动时,只受到指向圆盘圆心的摩擦力 C、图丙中汽车过拱桥最高点时,速度越大,对桥面的压力越小 D、图丁中若轿车转弯时速度过大发生侧翻,是因为需要的向心力大于提供的向心力三、非选择题
-
25. 如图,一雪块从倾角的屋顶上的点由静止开始下滑,滑到A点后离开屋顶。O、A间距离 , A点距地面的高度 , 雪块与屋顶的动摩擦因数。不计空气阻力,雪块质量不变,取 , 重力加速度大小。求:
 (1)、雪块从A点离开屋顶时的速度大小;(2)、雪块落地时的速度大小 , 及其速度方向与水平方向的夹角。26. 如图,M、N为固定在竖直平面内同一高度的两根细钉,间距。一根长为的轻绳一端系在M上,另一端竖直悬挂质量的小球,小球与水平地面接触但无压力。时,小球以水平向右的初速度开始在竖直平面内做圆周运动。小球牵引着绳子绕过N、M,运动到M正下方与M相距L的位置时,绳子刚好被拉断,小球开始做平抛运动。小球可视为质点,绳子不可伸长,不计空气阻力,重力加速度g取。
(1)、雪块从A点离开屋顶时的速度大小;(2)、雪块落地时的速度大小 , 及其速度方向与水平方向的夹角。26. 如图,M、N为固定在竖直平面内同一高度的两根细钉,间距。一根长为的轻绳一端系在M上,另一端竖直悬挂质量的小球,小球与水平地面接触但无压力。时,小球以水平向右的初速度开始在竖直平面内做圆周运动。小球牵引着绳子绕过N、M,运动到M正下方与M相距L的位置时,绳子刚好被拉断,小球开始做平抛运动。小球可视为质点,绳子不可伸长,不计空气阻力,重力加速度g取。 (1)、求绳子被拉断时小球的速度大小,及绳子所受的最大拉力大小;(2)、求小球做平抛运动时抛出点到落地点的水平距离;(3)、若在时,只改变小球的初速度大小,使小球能通过N的正上方且绳子不松弛,求初速度的最小值。27. 一匀强磁场分布在以O为圆心,半径为R的圆形区域内,方向与纸面垂直,如图所示,质量为m、电荷量q的带正电的质点,经电场加速后,以速度v沿半径MO方向进入磁场,沿圆弧运动到N点,然后离开磁场, , 质点所受重力不计,求:
(1)、求绳子被拉断时小球的速度大小,及绳子所受的最大拉力大小;(2)、求小球做平抛运动时抛出点到落地点的水平距离;(3)、若在时,只改变小球的初速度大小,使小球能通过N的正上方且绳子不松弛,求初速度的最小值。27. 一匀强磁场分布在以O为圆心,半径为R的圆形区域内,方向与纸面垂直,如图所示,质量为m、电荷量q的带正电的质点,经电场加速后,以速度v沿半径MO方向进入磁场,沿圆弧运动到N点,然后离开磁场, , 质点所受重力不计,求:(1)判断磁场的方向;
(2)该匀强磁场的磁感应强度B;
(3)带电质点在磁场中运动的时间。
 28. 如图所示,一轨道由半径R=2m的四分之一竖直圆弧轨道AB和水平直轨道BC在B点平滑连接而成.现有一质量为m=1kg 的小球M从A点正上方处的点由静止释放,小球M经过圆弧上的B点时,轨道对小球M的支持力大小。若在B处静止的放完全相同的小球N,两者发生弹性碰撞.碰后从C点水平飞离轨道,落到水平地面上的P点。已知B点与地面间的高度 , 小球与BC段轨道间的动摩擦因数 , 小球运动过程中可视为质点. (不计空气阻力,g取10 m/s2).求:
28. 如图所示,一轨道由半径R=2m的四分之一竖直圆弧轨道AB和水平直轨道BC在B点平滑连接而成.现有一质量为m=1kg 的小球M从A点正上方处的点由静止释放,小球M经过圆弧上的B点时,轨道对小球M的支持力大小。若在B处静止的放完全相同的小球N,两者发生弹性碰撞.碰后从C点水平飞离轨道,落到水平地面上的P点。已知B点与地面间的高度 , 小球与BC段轨道间的动摩擦因数 , 小球运动过程中可视为质点. (不计空气阻力,g取10 m/s2).求: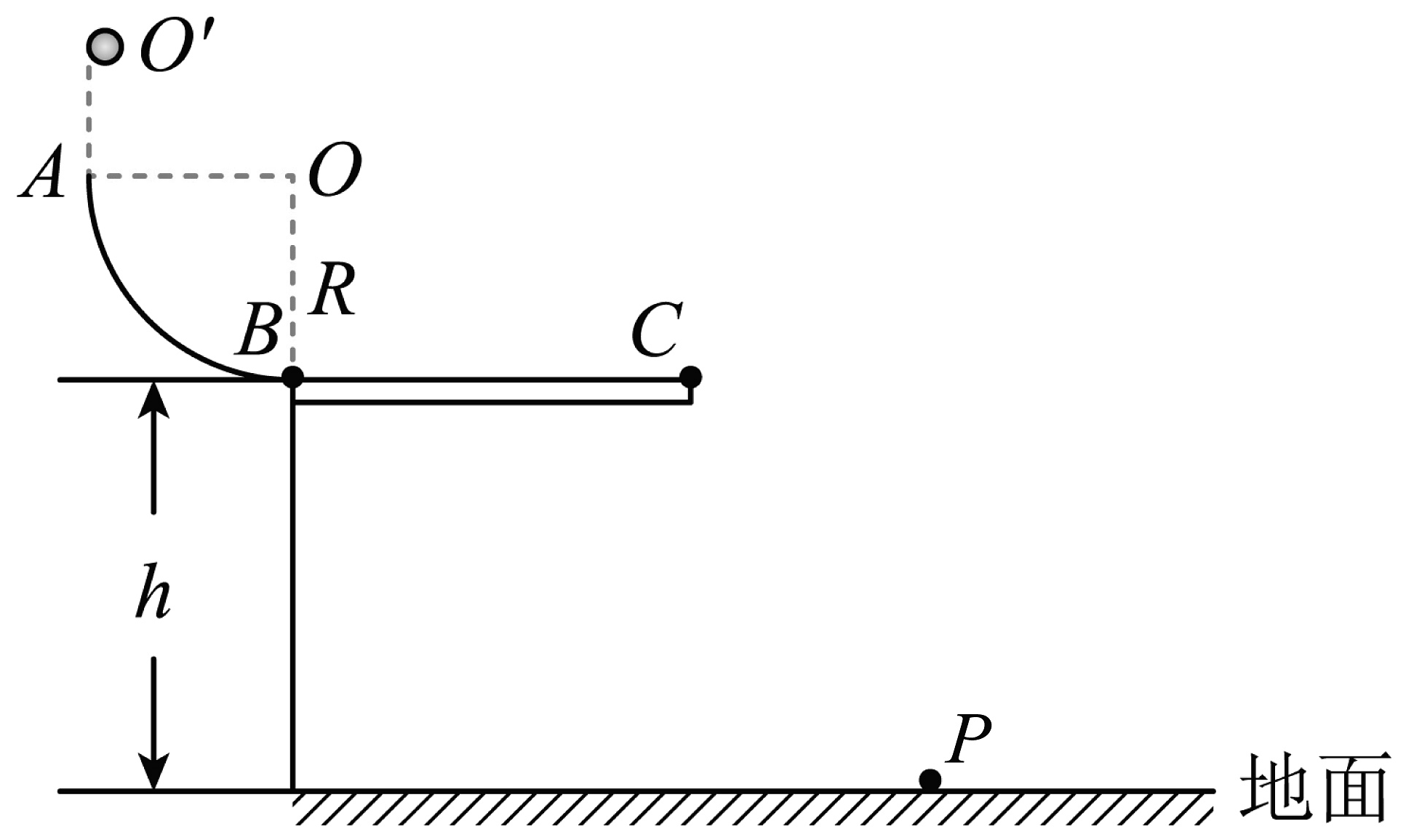 (1)、小球M运动至B点时的速度大小(2)、小球M在圆弧轨道AB上运动过程中克服摩擦力所做的功(3)、水平轨道BC的长度L=3m,小球从B点到落地过程重力的冲量?29. 质点在以某点为圆心半径为r的圆周上运动,即质点运动时其轨迹是圆周的运动叫“圆周运动”。它是一种最常见的曲线运动。例如电动机转子、车轮、皮带轮等都作圆周运动。如图所示,在竖直平面内有一光滑圆形轨道,a为轨道最低点,c为轨道最高点,b点、d点为轨道上与圆心等高的两点,e为段的中点。一个质量为m的小物块在轨道内侧做圆周运动。
(1)、小球M运动至B点时的速度大小(2)、小球M在圆弧轨道AB上运动过程中克服摩擦力所做的功(3)、水平轨道BC的长度L=3m,小球从B点到落地过程重力的冲量?29. 质点在以某点为圆心半径为r的圆周上运动,即质点运动时其轨迹是圆周的运动叫“圆周运动”。它是一种最常见的曲线运动。例如电动机转子、车轮、皮带轮等都作圆周运动。如图所示,在竖直平面内有一光滑圆形轨道,a为轨道最低点,c为轨道最高点,b点、d点为轨道上与圆心等高的两点,e为段的中点。一个质量为m的小物块在轨道内侧做圆周运动。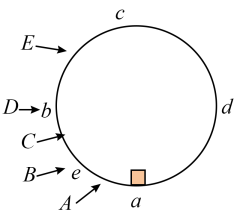 (1)、若物块从a点运动到c点所用时间为 , 则在时,物块在( )A、A段 B、B点 C、C段 D、D点 E、E段(2)、若物块在a点的速度为 , 经过时间t刚好到达b点,则在该过程中轨道对物块的支持力的冲量为( )A、 B、 C、 D、(3)、若物块质量为 , 下图是物块的速度v与物块和圆心连线转过的夹角的关系图像。
(1)、若物块从a点运动到c点所用时间为 , 则在时,物块在( )A、A段 B、B点 C、C段 D、D点 E、E段(2)、若物块在a点的速度为 , 经过时间t刚好到达b点,则在该过程中轨道对物块的支持力的冲量为( )A、 B、 C、 D、(3)、若物块质量为 , 下图是物块的速度v与物块和圆心连线转过的夹角的关系图像。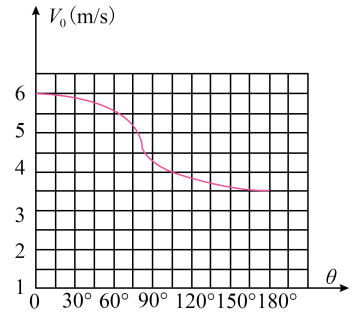
①求轨道半径R;
②求时,物块克服重力做功的瞬时功率P。
30. 一长为 的薄木板A放在倾角为 的光滑斜坡上,斜坡底端O到水平地面高度为 ,木板下端放一小物块B,物块可视为质点,开始木板通过销钉固定,物块与木板间的摩擦因数为 ,木板质量为 ,物块的质量 ,在撤去销钉的同时对木板施加沿斜面向下的 的拉力,作用一段时间后撤去拉力,之后物块恰能滑离木板,当物块从底端O滑出后落地点到O点的水平距离为 , ,求: (1)、拉力作用下物块B与木板A的加速度大;(2)、拉力的作用时间;(3)、物块滑离木板时的速度大小;(4)、物块滑离木板时到斜面底端的距离。31. 一光滑圆锥固定在水平地面上,其圆锥角为74°,圆锥底面的圆心为O。用一根长为0.5m的轻绳一端系一质量为0.1kg的小球(可视为质点),另一端固定在光滑圆锥顶上O点,O点距地面高度为0.75m,如图所示,如果使小球在光滑圆锥表面上做圆周运动。
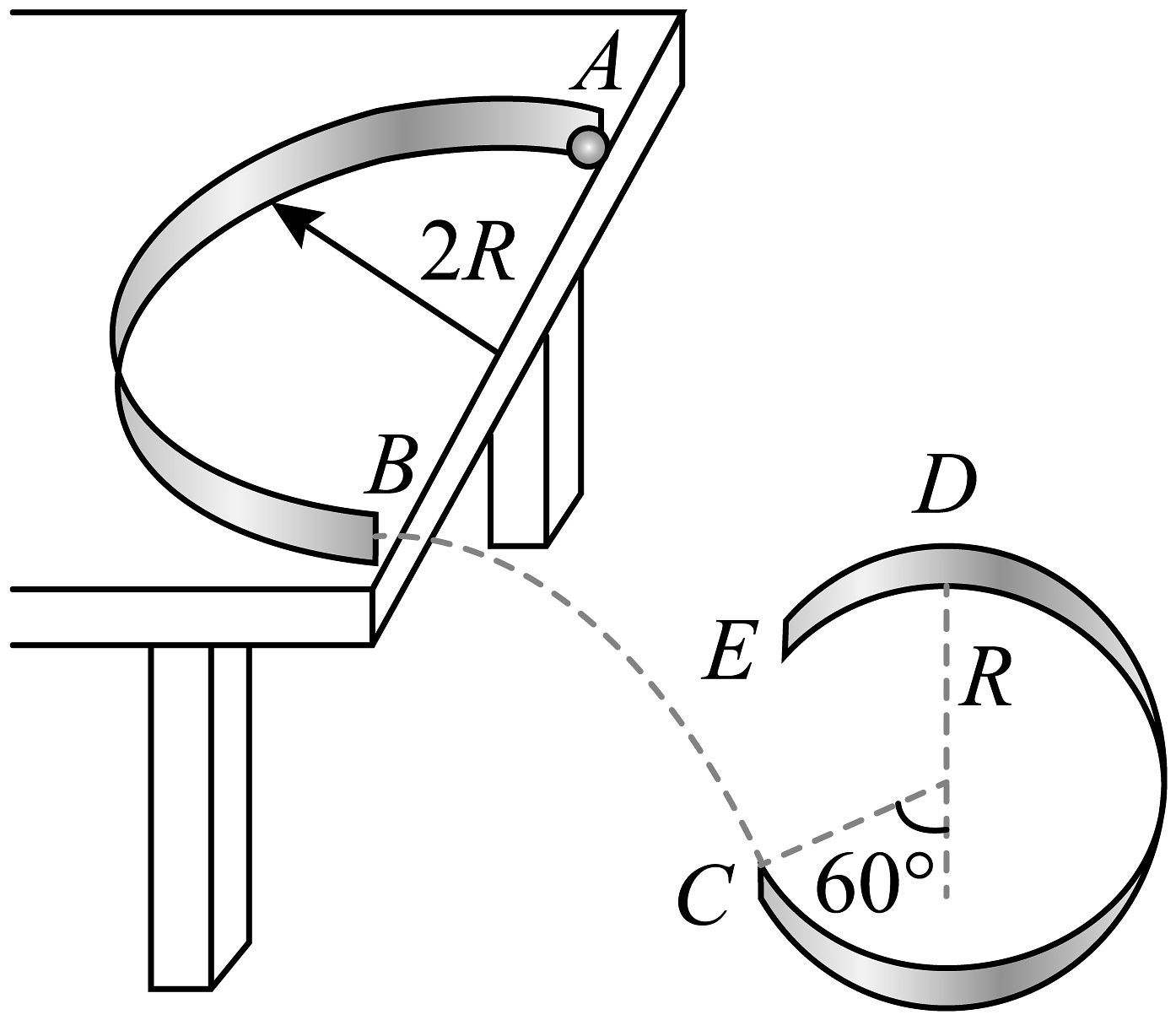
(1)、拉力作用下物块B与木板A的加速度大;(2)、拉力的作用时间;(3)、物块滑离木板时的速度大小;(4)、物块滑离木板时到斜面底端的距离。31. 一光滑圆锥固定在水平地面上,其圆锥角为74°,圆锥底面的圆心为O。用一根长为0.5m的轻绳一端系一质量为0.1kg的小球(可视为质点),另一端固定在光滑圆锥顶上O点,O点距地面高度为0.75m,如图所示,如果使小球在光滑圆锥表面上做圆周运动。 (1)、当小球静止时,此时细绳的拉力(2)、当小球的角速度不断增大,求小球恰离开圆锥表面时的角速度和此时细绳的拉力(3)、逐渐增加小球的角速度,若轻绳受力为N时会被拉断,求当轻绳断裂后小球做平抛运动的水平位移(取g=10m/s2,sin37°=0.6,cos37°=0.8,)32. 如图为某游戏装置原理示意图。在桌面上固定一半圆形竖直挡板,其半径为2R、内表面光滑,挡板的两端A、B在桌面边缘,B与半径为R的固定在地面上的光滑竖直圆弧轨道在同一竖直平面内,过C点的轨道半径与竖直方向的夹角为60°。小球以的水平初速度由A点切入挡板内侧,从B点飞出桌面后,在C点沿圆弧切线方向进入轨道内侧,并恰好能到达轨道的最高点D。已知重力加速度大小为g,忽略空气阻力,小球质量为m可视为质点。求:
(1)、当小球静止时,此时细绳的拉力(2)、当小球的角速度不断增大,求小球恰离开圆锥表面时的角速度和此时细绳的拉力(3)、逐渐增加小球的角速度,若轻绳受力为N时会被拉断,求当轻绳断裂后小球做平抛运动的水平位移(取g=10m/s2,sin37°=0.6,cos37°=0.8,)32. 如图为某游戏装置原理示意图。在桌面上固定一半圆形竖直挡板,其半径为2R、内表面光滑,挡板的两端A、B在桌面边缘,B与半径为R的固定在地面上的光滑竖直圆弧轨道在同一竖直平面内,过C点的轨道半径与竖直方向的夹角为60°。小球以的水平初速度由A点切入挡板内侧,从B点飞出桌面后,在C点沿圆弧切线方向进入轨道内侧,并恰好能到达轨道的最高点D。已知重力加速度大小为g,忽略空气阻力,小球质量为m可视为质点。求:(1)小球到达D点的速度大小;
(2)小球到达C点时,小球对轨道压力的大小;
(3)水平桌面的摩擦因数。
 33. 如图甲,水平地面上有A、B两个物块,两物块质量均为0.2kg,A与地面动摩擦因数为 , B与地面无摩擦,两物块用弹簧置于外力F的作用下向右前进,F与位移x的图如图乙所示,P为圆弧最低点,M为最高点,水平地面长度大于4m。
33. 如图甲,水平地面上有A、B两个物块,两物块质量均为0.2kg,A与地面动摩擦因数为 , B与地面无摩擦,两物块用弹簧置于外力F的作用下向右前进,F与位移x的图如图乙所示,P为圆弧最低点,M为最高点,水平地面长度大于4m。 (1)、求 , F做的功;(2)、时,A与B之间的弹力;(3)、要保证B能到达M点,圆弧半径满足的条件。34. 如图所示,在平面内的区域有竖直向下、大小为的匀强电场,在区域有以轴为中心轴、半径为、高为的圆筒,筒内分布着方向竖直向上、大小的匀强磁场,顶部平面与平面重合,圆心处开有小孔,圆筒底面涂有荧光粉,带电粒子到达处会发出荧光。在平面内有一粒子发射带 , 其两端坐标:、 , 之间各点均可在平面内向轴发射不同速率带正电的粒子。已知粒子质量为 , 电荷量为 , 圆筒接地,碰到圆筒的粒子即被导走,不计重力,不考虑场的边界效应及粒子间相互作用。
(1)、求 , F做的功;(2)、时,A与B之间的弹力;(3)、要保证B能到达M点,圆弧半径满足的条件。34. 如图所示,在平面内的区域有竖直向下、大小为的匀强电场,在区域有以轴为中心轴、半径为、高为的圆筒,筒内分布着方向竖直向上、大小的匀强磁场,顶部平面与平面重合,圆心处开有小孔,圆筒底面涂有荧光粉,带电粒子到达处会发出荧光。在平面内有一粒子发射带 , 其两端坐标:、 , 之间各点均可在平面内向轴发射不同速率带正电的粒子。已知粒子质量为 , 电荷量为 , 圆筒接地,碰到圆筒的粒子即被导走,不计重力,不考虑场的边界效应及粒子间相互作用。 (1)、若从点偏离水平方向向右下方发射的粒子恰能通过点进入磁场,求该粒子发射的速度;(2)、在某次发射中,从两点水平发射的粒子穿过点到达了圆筒底部,求它们发光点点的坐标;(3)、若发射带各点持续水平发射粒子,部分粒子穿过进入磁场,请通过分析,在乙图中画出荧光屏上的图案。35. 一游戏装置的竖直截面如图所示。倾斜直轨道AB、半径为R的竖直螺旋轨道、水平轨道BC和、倾角为的倾斜直轨道EF平滑连接成一个抛体装置。该装置除EF段轨道粗糙外,其余各段均光滑,F点与水平高台GHI等高。游戏开始,一质量为m的滑块1从轨道AB上的高度h处静止滑下,与静止在C点、质量也为m的滑块2发生完全非弹性碰撞后组合成滑块3,滑上滑轨。若滑块3落在GH段,反弹后水平分速度保持不变,竖直分速度减半;若滑块落在H点右侧,立即停止运动。已知 , EF段长度 , FG间距 , GH间距 , HI间距 , EF段。滑块1、2、3均可视为质点,不计空气阻力, , 。
(1)、若从点偏离水平方向向右下方发射的粒子恰能通过点进入磁场,求该粒子发射的速度;(2)、在某次发射中,从两点水平发射的粒子穿过点到达了圆筒底部,求它们发光点点的坐标;(3)、若发射带各点持续水平发射粒子,部分粒子穿过进入磁场,请通过分析,在乙图中画出荧光屏上的图案。35. 一游戏装置的竖直截面如图所示。倾斜直轨道AB、半径为R的竖直螺旋轨道、水平轨道BC和、倾角为的倾斜直轨道EF平滑连接成一个抛体装置。该装置除EF段轨道粗糙外,其余各段均光滑,F点与水平高台GHI等高。游戏开始,一质量为m的滑块1从轨道AB上的高度h处静止滑下,与静止在C点、质量也为m的滑块2发生完全非弹性碰撞后组合成滑块3,滑上滑轨。若滑块3落在GH段,反弹后水平分速度保持不变,竖直分速度减半;若滑块落在H点右侧,立即停止运动。已知 , EF段长度 , FG间距 , GH间距 , HI间距 , EF段。滑块1、2、3均可视为质点,不计空气阻力, , 。 (1)、若 , 求碰撞后瞬间滑块3的速度大小;(2)、若滑块3恰好能通过圆轨道 , 求高度h;(3)、若滑块3最终落入I点的洞中,则游戏成功。讨论游戏成功的高度h。36. 如图,一质量m=0.4kg的滑块(可视为质点)静止于动摩擦因数的水平轨道上的A点。对滑块施加一水平外力,使其向右运动,外力的功率恒为P=10W。经过一段时间后撤去外力,滑块继续滑行至B点后水平飞出,恰好在C点沿切线方向进入固定在竖直平面内的光滑圆弧形轨道,轨道的最低点D处装有压力传感器,当滑块到达传感器上方时,传感器的示数为25.6N。已知轨道AB的长度L=2.0m,半径OC和竖直方向的夹角 , 圆形轨道的半径R=0.5m。(空气阻力可忽略,g=10m/s2 , sin37°=0.6,cos37°=0.8)求:
(1)、若 , 求碰撞后瞬间滑块3的速度大小;(2)、若滑块3恰好能通过圆轨道 , 求高度h;(3)、若滑块3最终落入I点的洞中,则游戏成功。讨论游戏成功的高度h。36. 如图,一质量m=0.4kg的滑块(可视为质点)静止于动摩擦因数的水平轨道上的A点。对滑块施加一水平外力,使其向右运动,外力的功率恒为P=10W。经过一段时间后撤去外力,滑块继续滑行至B点后水平飞出,恰好在C点沿切线方向进入固定在竖直平面内的光滑圆弧形轨道,轨道的最低点D处装有压力传感器,当滑块到达传感器上方时,传感器的示数为25.6N。已知轨道AB的长度L=2.0m,半径OC和竖直方向的夹角 , 圆形轨道的半径R=0.5m。(空气阻力可忽略,g=10m/s2 , sin37°=0.6,cos37°=0.8)求:(1)滑块运动到C点时速度vc的大小;
(2)B、C两点的高度差h及水平距离x;
(3)水平外力作用在滑块上的时间t。
 37. 如图为一弹射游戏装置,它由安装在水平台面上的固定弹射器,水平直轨道AB,圆心为O的水平半圆细管道BCD,水平直轨道DE、FG、HI和逆时针转动的传送带EF等组成。木板静止在HI上,其上表面与FG相平,左端紧靠竖直边GH。游戏时滑块由A点弹出,经过轨道AB、管道BCD、轨道DE、传送带EF和轨道FG后,滑上木板。已知可视为质点的滑块质量 , 轨道DE长度 , 传送带长度 , 速度大小 , 木板质量 , 长度 , BCD的半径 , 滑块与轨道DE、传送带及木板间的动摩擦因数均为 , 木板与轨道HI间的动摩擦因数 , 其余各处均光滑,不考虑弹射过程中能量损失,各轨道间平滑连接。
37. 如图为一弹射游戏装置,它由安装在水平台面上的固定弹射器,水平直轨道AB,圆心为O的水平半圆细管道BCD,水平直轨道DE、FG、HI和逆时针转动的传送带EF等组成。木板静止在HI上,其上表面与FG相平,左端紧靠竖直边GH。游戏时滑块由A点弹出,经过轨道AB、管道BCD、轨道DE、传送带EF和轨道FG后,滑上木板。已知可视为质点的滑块质量 , 轨道DE长度 , 传送带长度 , 速度大小 , 木板质量 , 长度 , BCD的半径 , 滑块与轨道DE、传送带及木板间的动摩擦因数均为 , 木板与轨道HI间的动摩擦因数 , 其余各处均光滑,不考虑弹射过程中能量损失,各轨道间平滑连接。 (1)、若弹簧的弹性势能 , 求滑块运动到管道最高点时,受到的管道作用力大小;(2)、若滑块最终静止在轨道DE某处,求弹簧的弹性势能的范围;(3)、若弹簧的弹性势能 , 求木板运动的位移x。
(1)、若弹簧的弹性势能 , 求滑块运动到管道最高点时,受到的管道作用力大小;(2)、若滑块最终静止在轨道DE某处,求弹簧的弹性势能的范围;(3)、若弹簧的弹性势能 , 求木板运动的位移x。