第二章《分式》基础卷——湘教版（2024）数学八（上）单元分层测

试卷更新日期：2025-08-23 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 若式子 $\frac{2}{1 - x}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x > 1$ B、 $x \leq 1$ C、 $x \neq 1$ D、 $x < 1$

查看试题解析
2. 下列各式： $\frac{1}{x}$ ， $\frac{x}{3}$ ， $\frac{4}{3 b^{2} + 5}$ ， $\frac{5}{π}$ ， $- \frac{7 x y}{x^{2}}$ 是分式的有（）个。

A、1 B、2 C、3 D、4

查看试题解析
3. 2025年5月19日，央视新闻发布某国产品牌实现3nm（即0.000000003m）芯片研发设计突破，数0.000000003用科学记数法表示为（）

A、 $3 \times 1 0^{- 9}$ B、 $3 \times 1 0^{- 10}$ C、 $3 \times 1 0^{9}$ D、 $3 \times 1 0^{10}$

查看试题解析
4. 若把分式 $\frac{x + y}{2 x y}$ 中的 $x$ 和 $y$ 都扩大到原来的 $3$ 倍，且 $x + y \neq 0$ ，那么分式的值（）

A、扩大到原来的 $3$ 倍 B、不变 C、缩小到原来的 $\frac{1}{3}$ D、缩小到原来的 $\frac{1}{6}$

查看试题解析
5. 下列各式是最简分式的是（）

A、 $\frac{4 y + 2 x}{4 a}$ B、 $\frac{y - x}{x - y}$ C、 $\frac{x^{2} + 1}{x - 1}$ D、 $\frac{x^{2} - 1}{x + 1}$

查看试题解析
6. 下列代数式中，是最简分式的是（）

A、 $\frac{x}{2}$ B、 $\frac{2 x^{2} + x}{x^{2}}$ C、 $\frac{6}{4 x}$ D、 $\frac{1}{3 - x}$

查看试题解析
7. 已知 $a^{n - m} = 2$ ， $a^{n} = 8$ ，则 $a^{m}$ 的值为（）

A、-6 B、 $\frac{1}{4}$ C、4 D、6

查看试题解析
8. 已知关于 $x$ 的分式方程 $\frac{a}{x - 5} + \frac{2}{5 - x} = 1$ 的解是非负数，则 $a$ 的取值范围是（）

A、 $a \geq - 3$ B、 $a \leq - 3$ C、 $a > - 3$ 且 $a \neq 2$ D、 $a \geq - 3$ 且 $a \neq 2$

查看试题解析
9. 为扎实推进“五育”并举工作，加强劳动教育，某校投入2万元购进了一批劳动工具．开展课后服务后，学生的劳动实践需求明显增强，需再次采购一批相同的劳动工具，已知采购数量与第一次相同，但采购单价比第一次降低15元，总费用降低了 $10 %$ ．设第二次采购单价为 $x$ 元，则所列方程正确的是（）

A、 $\frac{20000}{x - 15} = \frac{20000 (1 - 10 %)}{x}$ B、 $\frac{20000}{x + 15} = \frac{20000 (1 - 10 %)}{x}$ C、 $\frac{20000}{x} = \frac{20000 (1 - 10 %)}{x - 15}$ D、 $\frac{20000}{x} = \frac{20000 (1 - 10 %)}{x + 15}$

查看试题解析
10. 在计算 $\frac{m^{2}}{m + 1} \div \frac{⨂}{m + 1}$ 时，把运算符号 “ $\div$ ”看成了 “+”，得到的计算结果是 $m$ ，则这道题的计算结果是（）

A、 $\frac{1}{m - 1}$ B、 $\frac{1}{m}$ C、 $m - 1$ D、 $m$

查看试题解析

二、填空题（每题3分，共24分）

11. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为零，则 $x$ 的值为．

查看试题解析
12. 若分式 $\frac{x}{x^{2} + 2}$ 的值为正，则实数 $x$ 的取值范围是.

查看试题解析
13. 分式 $\frac{1}{2 a b + 2 b^{2}}$ 与 $\frac{2 a}{a^{2} - b^{2}}$ 的最简公分母是

查看试题解析
14. 计算： $(\frac{x}{3 y})_{}^{2} =$ .

查看试题解析
15. $5^{x} = 18$ ， $5^{y} = 3$ ，则 $5^{x - 2 y} =$ ．

查看试题解析
16. 分式方程 $\frac{1}{x - 3} + 1 = \frac{m x}{x - 3}$ 无解，则m的值为.

查看试题解析
17. 如图，点A，B在数轴上所对应的数分别为 $- 3$ 和 $\frac{a}{a - 2}$ ，且点A，B到原点的距离相等，则a的值为．

查看试题解析
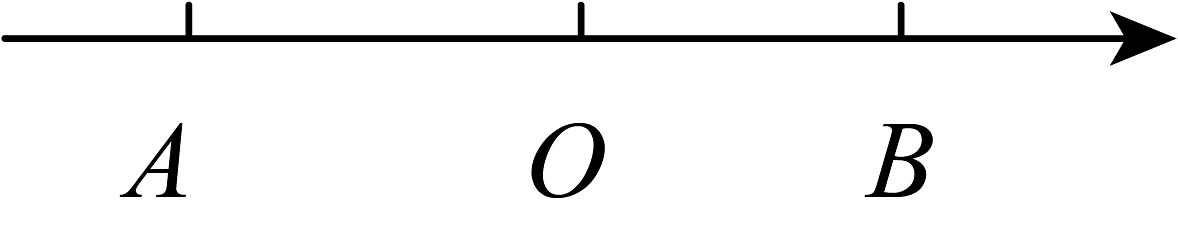18. 若关于x的分式方程 $\frac{a + 1}{x - 3} + \frac{x}{3 - x} = 1$ 解为整数，且关于y的一元一次不等式组 $\{\begin{array}{l} a - y \leq 7 y - 2 \\ \frac{5 y + 3}{2} > 3 y - 1 \end{array}$ 有且仅有4个整数解，那么符合条件的所有整数a的和为．

查看试题解析

三、解答题（共8题，共66分）

19. 计算：

(1)、 ${(π - 3.14)}^{0} + {(\frac{1}{2})}^{- 1} + {(- 1)}^{2023}$ ；

(2)、 $\sqrt{9} - \sqrt[3]{8} + {(π - 3)}^{0}$ ．

查看试题解析
20. 解下列方程：

(1)、 $\frac{2 x - 3}{x + 6} = \frac{1}{3};$

(2)、 $\frac{6}{1 - x^{2}} = \frac{3}{1 - x} 。$

查看试题解析
21. 计算：

(1)、 $\frac{2 a}{a + 4} \cdot \frac{a^{2} + 8 a + 16}{4 a^{2}}$ ；

(2)、 $(x^{2} - 2 x) \div \frac{x - 2}{2 x}$ ．

查看试题解析
22. 已知分式 $\frac{x + 1}{x - 5} ，$ 求：

(1)、当x为何值时，分式有意义?

(2)、当x为何值时，分式的值为0?

(3)、当x=0，1，2时，分式的值.

查看试题解析
23. 已知关于 $x$ 的方程 $\frac{x}{x - 1} + 1 = \frac{k x + 2}{1 - x}$ ，求：

(1)、当 $k$ 为何值时，方程会产生增根．

(2)、当 $k$ 为何值时，方程无解．

查看试题解析
24. 已知分式 $A = (a + 1 - \frac{3}{a - 1}) \div \frac{a^{2} - 4 a + 4}{a - 1}$

(1)、化简这个分式．

(2)、把分式A化简结果的分子与分母同时加上3后得到分式B，问：当a>2时，分式B的值较原来分式A的值是变大了还是变小了？试说明理由．

(3)、若A的值是整数，且a也为整数，求出所有符合条件的a的值．

查看试题解析
25. 为全面落实长沙市“三高四新”美好蓝图，市政府计划对城区道路进行改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的2倍，甲队改造400米的道路比乙队改造同样长的道路少用5天．

(1)、甲、乙两工程队每天能改造道路的长度分别是多少米？

(2)、若甲队工作一天需付费用5万元，乙队工作一天需付费用3万元，如需改造的道路全长1000米．改造总费用不超过65万元，至少安排甲队工作多少天？

查看试题解析
26. 我们规定两数a、b之间的一种运算，记作 $[a, b]$ ：如果 $a^{c} = b$ ，那么 $[a, b] = c$ ；例如 $2^{3} = 8$ ，记作 $[2, 8] = 3$ ，

(1)、根据以上规定求出： $[4, 64] =$ ______________； $[2024, 1] =$ ______________；

(2)、小明发现 $[5, 3] + [5, 4] = [5, 12]$ 也成立，并证明如下
设： $[5, 3] = x$ $[5, 4] = y$
$∴ 5^{x} = 3$ $5^{y} = 4$
$∵ 5^{x} \cdot 5^{y} = 5^{x + y} = 12$
$[5, 12] = x + y$
$∴ [5, 3] + [5, 4] = x + y = [5, 12]$
根据以上证明，请计算 $[2024, 6] + [2024, 7] = [2024$ ， ______________]

(3)、猜想 $[4, 14] - [4, 7] = [4$ ， ______________]，并说明理由．

查看试题解析

第二章 《分式》基础卷——湘教版（2024）数学八（上）单元分层测

一、选择题（每题3分，共30分）

二、填空题（每题3分，共24分）

三、解答题（共8题，共66分）

第二章《分式》基础卷——湘教版（2024）数学八（上）单元分层测