人教版(2024)八(上)数学第十三章单元质量检测培优卷
试卷更新日期:2025-08-20 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 直角三角形中两个锐角的平分线相交所成的钝角的度数为( )A、 B、 C、 D、 或2. 在探究证明“三角形的内角和等于”时,综合实践小组的同学作了如图四种辅助线,其中不能证明“三角形的内角和等于”的是( )
 A、如图①,过点作 B、如图②,延长到 , 过点作 C、如图③,过上一点作 , D、如图④,过点作3. 小明把一副直角三角尺按如图所示的方式摆放在一起,则等于( )
A、如图①,过点作 B、如图②,延长到 , 过点作 C、如图③,过上一点作 , D、如图④,过点作3. 小明把一副直角三角尺按如图所示的方式摆放在一起,则等于( ) A、 B、 C、 D、4. 如图,点D是边上的中点,点E是上一点且 , F、G是边上的三等分点,若四边形的面积为14,则的面积是( )
A、 B、 C、 D、4. 如图,点D是边上的中点,点E是上一点且 , F、G是边上的三等分点,若四边形的面积为14,则的面积是( ) A、24 B、42 C、48 D、565. 如图,△为直角三角形, , AD为∠CAB的平分线,与∠ABC的平分线BE交于点E , BG是△ABC的外角平分线,AD与BG相交于点G , 则∠ADC与∠GBF的和为( )
A、24 B、42 C、48 D、565. 如图,△为直角三角形, , AD为∠CAB的平分线,与∠ABC的平分线BE交于点E , BG是△ABC的外角平分线,AD与BG相交于点G , 则∠ADC与∠GBF的和为( ) A、120° B、135° C、150° D、160°6. 如图,在 中, , , , ,连接BC,CD,则 的度数是( )
A、120° B、135° C、150° D、160°6. 如图,在 中, , , , ,连接BC,CD,则 的度数是( )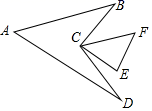 A、45° B、50° C、55° D、80°7. 如图,于点 , 点、分别是射线、上的动点(不与点重合),延长至点 , 的角平分线及其反向延长线分别交、的角平分线于点、.若中有一个角是另一个角的3倍,则为( ).
A、45° B、50° C、55° D、80°7. 如图,于点 , 点、分别是射线、上的动点(不与点重合),延长至点 , 的角平分线及其反向延长线分别交、的角平分线于点、.若中有一个角是另一个角的3倍,则为( ). A、或 B、或 C、或 D、或8. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )
A、或 B、或 C、或 D、或8. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )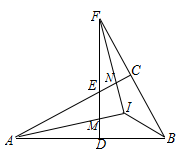 A、1个 B、2个 C、3个 D、4个9. 在直角三角形中, , 的平分线交于点 , 的平分线交于点 , 、相交于点 , 过点作 , 过点作于点 , 有以下结论:①;②;③平分;④ , 其中正确的个数是( )
A、1个 B、2个 C、3个 D、4个9. 在直角三角形中, , 的平分线交于点 , 的平分线交于点 , 、相交于点 , 过点作 , 过点作于点 , 有以下结论:①;②;③平分;④ , 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得;……以此类推得到 , 则的度数是( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得;……以此类推得到 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共5小题,每小题3分,共15分。
-
11. 若三角形的周长为13,且三边均为整数,则满足条件的三角形有种.12. △ABC中,∠A是最小角,∠B是最大角,且2∠B=5∠A,若∠B的最大值m°,最小值n°,则m+n=.13. 如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF= .
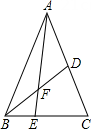 14. 如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF= (∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F= (∠BAC﹣∠C);其中正确的是 .
14. 如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF= (∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F= (∠BAC﹣∠C);其中正确的是 .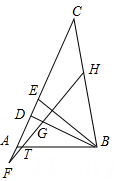 15. 如图1,六分仪是一种测量天体高度的航海仪器,观测者手持六分仪,可得出观测点的地理坐标.
15. 如图1,六分仪是一种测量天体高度的航海仪器,观测者手持六分仪,可得出观测点的地理坐标.在图2所示的“六分仪原理图”中,所观测星体记为S,两个反射镜面位于A,B两处,B处的镜面所在直线自动与刻度线保持平行(即),并与A处的镜面所在直线相交于点C,所在直线与水平线相交于点D, , 观测角=(用表示).


小贴士:
如图3,光线经过镜面反射时,反射角等于入射角,所以图2中 ,

三、解答题:本大题共8小题,共75分
-
16. 如图,线段与相交于 , 点、分别是延长线、延长线上一点.线段在内部,线段在内部.四边形始终为凸四边形,且有 , , 、均为正数.
 (1)、若 , , , , 如图1,求度数;(2)、若 , , , 如图2,则当变化时,为何值时,为与、无关的定值?(3)、若为定值,如图3,则和满足关系式______时,为与、无关的定值.17. 如图,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC于点E,点F在AE上且CF∥AD.
(1)、若 , , , , 如图1,求度数;(2)、若 , , , 如图2,则当变化时,为何值时,为与、无关的定值?(3)、若为定值,如图3,则和满足关系式______时,为与、无关的定值.17. 如图,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC于点E,点F在AE上且CF∥AD. (1)、如图①,若△ABC是锐角三角形,∠B=30°,∠ACB=80°,则∠CFE=度.(2)、如图①,若△ABC是锐角三角形,∠ACB>∠B,∠B=x,∠ACB=y,则∠CFE=(用含x,y的代数式表示).(3)、如图②,若△ABC是钝角三角形,∠ACB为钝角,其余条件不变,则(2)中的结论还成立吗?说明理由.18. 平面内的两条直线有相交和平行两种位置关系.
(1)、如图①,若△ABC是锐角三角形,∠B=30°,∠ACB=80°,则∠CFE=度.(2)、如图①,若△ABC是锐角三角形,∠ACB>∠B,∠B=x,∠ACB=y,则∠CFE=(用含x,y的代数式表示).(3)、如图②,若△ABC是钝角三角形,∠ACB为钝角,其余条件不变,则(2)中的结论还成立吗?说明理由.18. 平面内的两条直线有相交和平行两种位置关系. (1)、如图①,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;(2)、在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)(3)、根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.19. △ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)、如图①,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;(2)、在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)(3)、根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.19. △ABC中,AD是∠BAC的角平分线,AE是△ABC的高. (1)、如图1,若∠B=40°,∠C=60°.求∠DAE的度数.(2)、如图2(∠B<∠C),试说明∠DAE与∠B、∠C的数量关系.(3)、拓展:如图3,四边形ABDC中,AE是∠BAC的角平分线,DA是∠BDC的角平分线,猜想:∠DAE与∠B、∠C的数量关系是否改变,说明理由.20. 如图 , 在中,与的平分线相交于点 .
(1)、如图1,若∠B=40°,∠C=60°.求∠DAE的度数.(2)、如图2(∠B<∠C),试说明∠DAE与∠B、∠C的数量关系.(3)、拓展:如图3,四边形ABDC中,AE是∠BAC的角平分线,DA是∠BDC的角平分线,猜想:∠DAE与∠B、∠C的数量关系是否改变,说明理由.20. 如图 , 在中,与的平分线相交于点 . (1)、若 , 则的度数是 ;(2)、如图 , 作外角 , 的角平分线交于点 , 试探索 , 之间的数量关系;(3)、如图 , 延长线段 , 交于点 , 在中,存在一个内角等于另一个内角的倍,求的度数.21.
(1)、若 , 则的度数是 ;(2)、如图 , 作外角 , 的角平分线交于点 , 试探索 , 之间的数量关系;(3)、如图 , 延长线段 , 交于点 , 在中,存在一个内角等于另一个内角的倍,求的度数.21. (1)、【课本再现】如图1,在中,线经过点且 . 求证:;(2)、【变式演练】如图2,在中, , 点在边上,交于点 . 若 , 求的度数;(3)、【方法应用】如图3,直线与直线相交于点 , 夹角的锐角为 , 点在直线上且在点右侧,点在直线上且在直线上方,点在直线上且在点左侧运动,点在射线上运动(不与点重合).当时,平分平分交直线于点 , 求的度数.22. 请阅读下列材料,并完成相应的任务:
(1)、【课本再现】如图1,在中,线经过点且 . 求证:;(2)、【变式演练】如图2,在中, , 点在边上,交于点 . 若 , 求的度数;(3)、【方法应用】如图3,直线与直线相交于点 , 夹角的锐角为 , 点在直线上且在点右侧,点在直线上且在直线上方,点在直线上且在点左侧运动,点在射线上运动(不与点重合).当时,平分平分交直线于点 , 求的度数.22. 请阅读下列材料,并完成相应的任务:有趣的“飞镖图”
如图,这种形似飞镖的四边形,可以形象地称它为“飞镖图”.当我们仔细观察后发现,它实际上就是凹四边形.那么它具有哪些性质呢?又将怎样应用呢?下面我们进行认识与探究:凹四边形通俗地说,就是一个角“凹”进去的四边形,其性质有:凹四边形中最大内角外面的角等于其余三个内角之和.


(即如图 1,∠ADB=∠A+∠B+∠C )理由如下:
方法一:如图 2,连接 AB,则在△ABC 中,∠C+∠CAB+∠CBA=180°,即∠1+∠2+∠3+∠4+∠C=180°,又∵在△ABD 中,∠1+∠2+∠ADB=180°,∴∠ADB=∠3+∠4+∠C, 即∠ADB=∠CAD+∠CBD+∠C.
方法二:如图 3,连接 CD 并延长至 F,∵∠1 和∠3 分别是△ACD 和△BCD 的一个外角,. . . . . .
大家在探究的过程中,还发现有很多方法可以证明这一结论,你有自己的方法吗?
任务:
(1)、填空:“方法一”主要依据的一个数学定理是;(2)、探索:根据“方法二”中辅助线的添加方式,写出该证明过程的剩余部分;(3)、应用:如图 4,AE 是∠CAD 的平分线,BF 是∠CBD 的平分线,AE 与 BF 交于 G, 若∠ADB=150°,∠AGB=110°,请你直接写出∠C 的大小.23. 已知AB∥CD,点F、G分别在AB、CD上,且点E为射线FG上一点. (1)、如图1:当点E在线段FG上时,连接AE、DE,易得 .
(1)、如图1:当点E在线段FG上时,连接AE、DE,易得 .小明给出的理由是:如图1,过E作EH∥AE,
∵AB∥CD,
∴AB∥CD∥EH.(平行于同一条直线的两条直线互相平行)
∴ , , (依据1)
∴;(依据2)
填空:依据1: .
依据2: .
(2)、如图2,当点E在FG延长线上时,求证:;(3)、如图3,AI平分∠BAE,DI交AI于点I,交AE于点K,且 , , , 求∠EKD的度数.