人教版(2024)八(上)数学第十三章单元质量检测提升卷
试卷更新日期:2025-08-20 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 下列说法正确的是( )A、同位角相等 B、若三条线段的长a、b、c满足 , 则以a、b、c为边一定能组成三角形 C、两条直线被第三条直线所截,同旁内角互补 D、三角形的三条高至少有一条在三角形内2. 如图,在中,平分 . 则、、的数量关系为( )
 A、 B、 C、 D、3. 如图,已知点 , , 分别为 , , 的中点,若的面积为20,则四边形的面积为( )
A、 B、 C、 D、3. 如图,已知点 , , 分别为 , , 的中点,若的面积为20,则四边形的面积为( ) A、10 B、9 C、8.5 D、7.54. 如图, , 则等于( )
A、10 B、9 C、8.5 D、7.54. 如图, , 则等于( ) A、 B、 C、 D、5. 在下列条件:①;②;③;④中,能确定为直角三角形的条件有( )A、2个 B、3个 C、4个 D、5个6. 如图,在中,已知 , 点是的中点,且的面积为9,则的面积为( )
A、 B、 C、 D、5. 在下列条件:①;②;③;④中,能确定为直角三角形的条件有( )A、2个 B、3个 C、4个 D、5个6. 如图,在中,已知 , 点是的中点,且的面积为9,则的面积为( )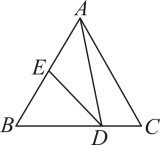 A、1 B、2 C、3 D、47. 如图,中,的三等分线分别与的平分线交于点 , , 若 , , 则的度数为( ).
A、1 B、2 C、3 D、47. 如图,中,的三等分线分别与的平分线交于点 , , 若 , , 则的度数为( ). A、 B、 C、 D、8. 已知a、b、c为三角形的三边,则化简后的值为( )A、 B、 C、 D、9. 如图,在中,平分 , 平分 , 与交于点 , 其中 , 则的度数为( )
A、 B、 C、 D、8. 已知a、b、c为三角形的三边,则化简后的值为( )A、 B、 C、 D、9. 如图,在中,平分 , 平分 , 与交于点 , 其中 , 则的度数为( )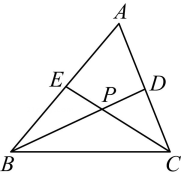 A、 B、 C、 D、10. 如图,中,是高,、是角平分线,交、于G、H, . 下列结论:①;②;③;④ . 其中正确的是( )
A、 B、 C、 D、10. 如图,中,是高,、是角平分线,交、于G、H, . 下列结论:①;②;③;④ . 其中正确的是( ) A、①② B、①③④ C、①②④ D、①②③④
A、①② B、①③④ C、①②④ D、①②③④二、填空题:本大题共5小题,每小题3分,共15分。
-
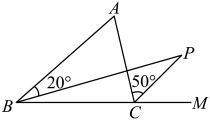
11. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P=.
 12. 如图,将沿经过点的直线折叠,使边所在的直线与边所在的直线重合,点落在边上的处,若 , , 则 .
12. 如图,将沿经过点的直线折叠,使边所在的直线与边所在的直线重合,点落在边上的处,若 , , 则 . 13. 在中,和是它的两条直角边,的平分线与的外角平分线交于点D , 则14. 当三角形中一个内角β是另外一个内角a的时,我们称此三角形为“友好三角形”. 如果一个“友好三角形”中有一个内角为 , 那么这个“友好三角形”的“友好角a”的度数为 .15. 一个零件的形状如图所示,按规定应等于 . 已知 , 分别是和 , 李伯伯量得 , 则这个零件是否合格? . (填“合格”或“不合格)
13. 在中,和是它的两条直角边,的平分线与的外角平分线交于点D , 则14. 当三角形中一个内角β是另外一个内角a的时,我们称此三角形为“友好三角形”. 如果一个“友好三角形”中有一个内角为 , 那么这个“友好三角形”的“友好角a”的度数为 .15. 一个零件的形状如图所示,按规定应等于 . 已知 , 分别是和 , 李伯伯量得 , 则这个零件是否合格? . (填“合格”或“不合格)
三、解答题:本大题共8小题,共75分
-
16. 如图,已知点O为内任意一点,证明: .
 17. 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
17. 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.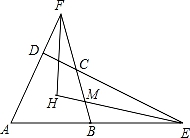 18. 如图1,在中,平分 .
18. 如图1,在中,平分 . (1)、若为线段上的一个点,过点作交线段的延长线于点 .
(1)、若为线段上的一个点,过点作交线段的延长线于点 .①若 , , 则 ;
②猜想与、之间的数量关系,并给出证明.
(2)、如图2,若在线段的延长线上,过点作交直线于点 , 请直接写出与、的数量关系.19. 若三角形的两个内角与满足 , 那么这样的三角形是“准互余三角形”. (1)、关于“准互余三角形”,下列说法中正确的是____________(填写所有正确说法的序号);
(1)、关于“准互余三角形”,下列说法中正确的是____________(填写所有正确说法的序号);①在中,若 , , , 则是“准余三角形”;
②若是“准互余三角形”, , , 则;
③“准互余三角形”一定是钝角三角形.
(2)、如图1,在中, , 是的角平分线,求证:是“准互余三角形”;(3)、如图2,B,C为直线l上两点,点A在直线l外,且 . 若P是直线l上一点,且是“准互余三角形”,请直接写出的度数.20. 中华人民共和国五星红旗上大五角星代表中国共产党,四颗小五角星代表工人、农民、小资产阶级和民族资产阶级四个阶级.五颗五角星互相连缀、疏密相间,象征中国人民大团结.每颗小星各有一个尖角正对大星中心点,表示人民对党的向心之意,如图①:根据图形填空: (1)、 , ;(2)、;(3)、【应用】
(1)、 , ;(2)、;(3)、【应用】如图②.求的度数.
21. 已知a、b、c为的三边长,且b、c满足 , a为方程的解,求的周长.22.(1)、已知:如图①的图形我们把它称为“8字形”,试说明: .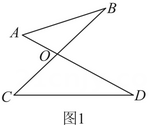 (2)、如图②,分别平分 , 若 , 求的度数.
(2)、如图②,分别平分 , 若 , 求的度数.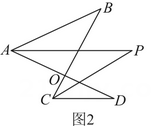 (3)、如图③,直线平分 , 平分的外角 , 猜想与的数量关系并证明.
(3)、如图③,直线平分 , 平分的外角 , 猜想与的数量关系并证明.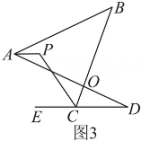 23. 如图①,△ABC的角平分线BD、CE相交于点P.
23. 如图①,△ABC的角平分线BD、CE相交于点P. (1)、如果∠A=80°,求∠BPC的度数;(2)、如图②,过P点作直线MN,分别交AB和AC于点M和N,且MN平行于BC,则有∠MPB+∠NPC=90°∠A.若将直线MN绕点P旋转,
(1)、如果∠A=80°,求∠BPC的度数;(2)、如图②,过P点作直线MN,分别交AB和AC于点M和N,且MN平行于BC,则有∠MPB+∠NPC=90°∠A.若将直线MN绕点P旋转,(ⅰ)如图③,试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立,并说明理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(ⅰ)中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立?若不成立,请给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.