人教版(2024)八(上)数学第十三章单元质量检测基础卷
试卷更新日期:2025-08-20 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 如图,△ABC的边BC上的高是( )
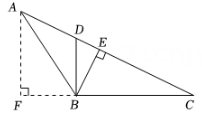 A、线段AF B、线段DB C、线段CF D、线段BE2. 下列各组线段中,首尾相接不能组成三角形的是( )A、12cm,8cm,5cm B、12cm,8cm,6cm C、12cm,5cm,6cm D、8cm,5cm,6cm3. 已知中, , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定4. 如图是折叠凳及其侧面示意图.若 , 则折叠凳的宽可能为( ).
A、线段AF B、线段DB C、线段CF D、线段BE2. 下列各组线段中,首尾相接不能组成三角形的是( )A、12cm,8cm,5cm B、12cm,8cm,6cm C、12cm,5cm,6cm D、8cm,5cm,6cm3. 已知中, , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定4. 如图是折叠凳及其侧面示意图.若 , 则折叠凳的宽可能为( ). A、 B、 C、 D、5. 如图,在锐角中,为边上的中线,则( )
A、 B、 C、 D、5. 如图,在锐角中,为边上的中线,则( ) A、 B、 C、 D、6. 如图,∠1=100°,∠C=70°,则∠A的大小是( )
A、 B、 C、 D、6. 如图,∠1=100°,∠C=70°,则∠A的大小是( ) A、10° B、20° C、30° D、80°7. 自行车支架一般都会采用如图的设计.这种方法应用的几何原理是( )
A、10° B、20° C、30° D、80°7. 自行车支架一般都会采用如图的设计.这种方法应用的几何原理是( )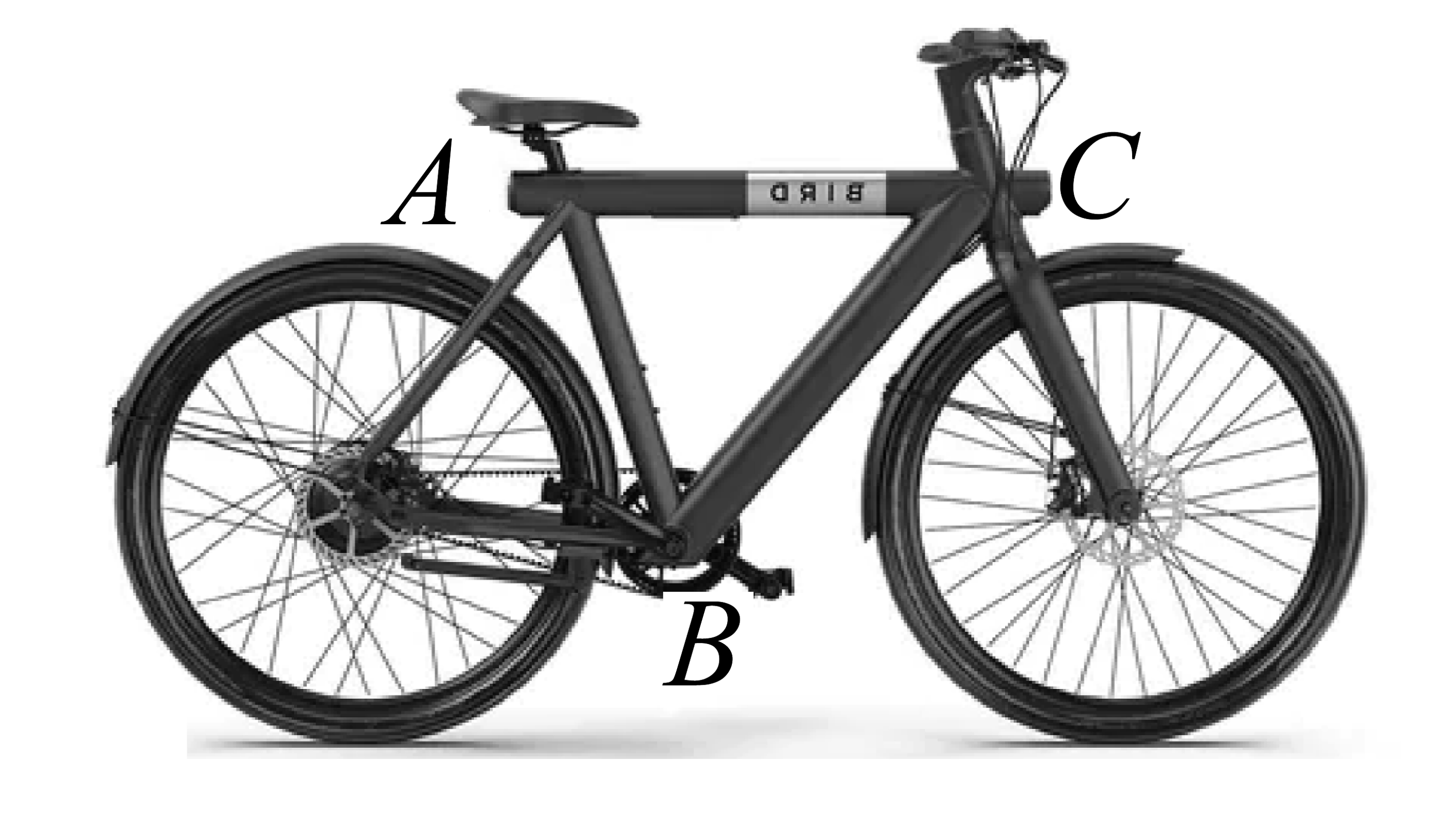 A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短8. 如图,在中,已知点D,E分别为边 , 上的中点,且 , 则的值为( )
A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短8. 如图,在中,已知点D,E分别为边 , 上的中点,且 , 则的值为( ) A、 B、 C、 D、9. 如图,是斜边上的高线, , 则( )
A、 B、 C、 D、9. 如图,是斜边上的高线, , 则( )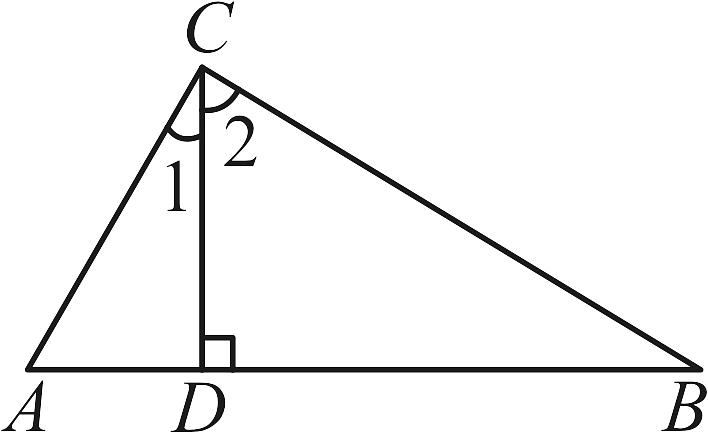 A、 B、 C、 D、10. 如图,在中, , 平分 , 若 , , 则的度数为( )
A、 B、 C、 D、10. 如图,在中, , 平分 , 若 , , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共5小题,每小题3分,共15分。
-
11. 已知的三个内角度数比为 , 则这个三角形是三角形.12. 中, , 那么与相邻的一个外角等于13. 已知三角形的三边长为3、7、a,且a为整数,则a的最大值为 .14. 将两张三角形纸片如图摆放,量得 , 则的度数是 .
 15. 如图,在中,已知点 , , 分别为边 , , 的中点,且的面积等于 , 则阴影部分图形面积等于 .
15. 如图,在中,已知点 , , 分别为边 , , 的中点,且的面积等于 , 则阴影部分图形面积等于 .
三、解答题:本大题共8小题,共75分
-
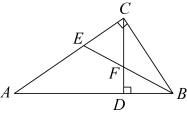
16. 已知:如图,在中,AB,BE平分分别交AC,CD于点E,F.求证:
 17. 如图,在四边形ABCD中,AB∥CD,E为BC上一点,且∠BAE=25°,∠CDE=65°.求证:△ADE是直角三角形.
17. 如图,在四边形ABCD中,AB∥CD,E为BC上一点,且∠BAE=25°,∠CDE=65°.求证:△ADE是直角三角形. 18. 如图,点D在AB上,点E在AC上,BE、CD相交于点O.
18. 如图,点D在AB上,点E在AC上,BE、CD相交于点O.(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
 19. 如图,在△ABC中,AD是BC边上的中线。已知 5cm,求△ABD与△ACD的周长的差。
19. 如图,在△ABC中,AD是BC边上的中线。已知 5cm,求△ABD与△ACD的周长的差。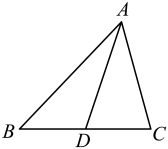 20.(1)、如图①,△ABC中,点D , E在边BC上,AD平分∠BAC , AE⊥BC , , ,求∠DAE的度数;
20.(1)、如图①,△ABC中,点D , E在边BC上,AD平分∠BAC , AE⊥BC , , ,求∠DAE的度数; (2)、如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其他条件不变,求∠F的度数.
(2)、如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其他条件不变,求∠F的度数. 21. 已知中,(1)、 , , 求、、的度数.(2)、 , , , 是三角形的三边长,且 , , , 都是整数.化简:22. 【问题呈现】
21. 已知中,(1)、 , , 求、、的度数.(2)、 , , , 是三角形的三边长,且 , , , 都是整数.化简:22. 【问题呈现】如图①,已知线段 , 相交于点 , 连结 , , 我们把形如这样的图形称为“字型”.
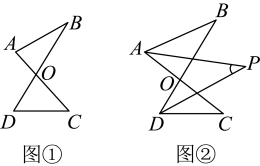 (1)、证明: .(2)、【问题探究】
(1)、证明: .(2)、【问题探究】继续探究,如图②,、分别平分、 , 、交于点 , 求与、之间的数量关系.为了研究这一问题,尝试代入、的值求的值,得到下面几组对应值:
表中 , 猜想得到与、的数量关系为;
(3)、证明()中猜想得到的与、的数量关系;(单位:度)
(单位:度)
(单位:度)
23. 阅读材料:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“优雅三角形”,其中称为“优雅角”.例如:一个三角形三个内角的度数分别是 , 这个三角形就是“优雅三角形”,其中“优雅角”的度数为;反之,若一个三角形是“优雅三角形”,则这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
(1)、一个“优雅三角形”的一个内角为 , 若“优雅角”为锐角,则这个“优雅角”的度数为;(2)、如图, , 在射线上取一点A,过点A作 , 交于点B,以A为端点画射线 , 交线段于点C(点C不与点O,B重合),得到一个以为“优雅角”的“优雅角三角形” , 求的度数.