沪科版(2024)数学八年级上册14.2全等三角形的判定同步分层练习
试卷更新日期:2025-08-19 类型:同步测试
一、夯实基础
-
1. 数学来源于生活,又服务于生活.以下四幅图中用数学原理解释不正确的是( )
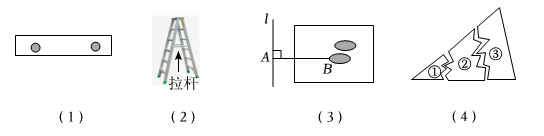 A、图(1)两钉子就能固定木条这样做的道理是利用了两点确定一条直线 B、图(2)人字梯中间一般会设计一根“拉杆”,这样做的道理是利用了三角形的稳定性 C、图(3)体育课堂测量跳远的成绩是利用了垂线段最短 D、图(4)一块三角形模具打碎为三块,只带编号为③的那一块碎片到商店去,就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法SAS2. 下面是“作一个角使其等于”的尺规作图方法.
A、图(1)两钉子就能固定木条这样做的道理是利用了两点确定一条直线 B、图(2)人字梯中间一般会设计一根“拉杆”,这样做的道理是利用了三角形的稳定性 C、图(3)体育课堂测量跳远的成绩是利用了垂线段最短 D、图(4)一块三角形模具打碎为三块,只带编号为③的那一块碎片到商店去,就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法SAS2. 下面是“作一个角使其等于”的尺规作图方法.(1)如图,以点为圆心,任意长为半径画弧,分别交 , 于点 , ;
(2)作射线 , 以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,两弧交于点;
(3)过点作射线 , 则.

上述方法通过判定得到 , 其中判定的依据是( )
A、三边分别相等的两个三角形全等 B、两边及其夹角分别相等的两个三角形全等 C、两角及其夹边分别相等的两个三角形全等 D、两角分别相等且其中一组等角的对边相等的两个三角形全等3. 如图,且且 , 若点E、B、D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积是( )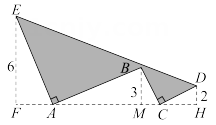 A、50 B、44 C、38 D、324. 如图,在中, , . 以A为圆心,为半径画弧交于点D;分别以C,D为圆心,大于长为半径画弧交于点E,射线交于点F,连结 , 则的度数为( )
A、50 B、44 C、38 D、324. 如图,在中, , . 以A为圆心,为半径画弧交于点D;分别以C,D为圆心,大于长为半径画弧交于点E,射线交于点F,连结 , 则的度数为( ) A、 B、 C、 D、5. 如图,已知点、、、在同一条直线上, , , 根据全等三角形的判定方法,下列能证明的条件是( )
A、 B、 C、 D、5. 如图,已知点、、、在同一条直线上, , , 根据全等三角形的判定方法,下列能证明的条件是( )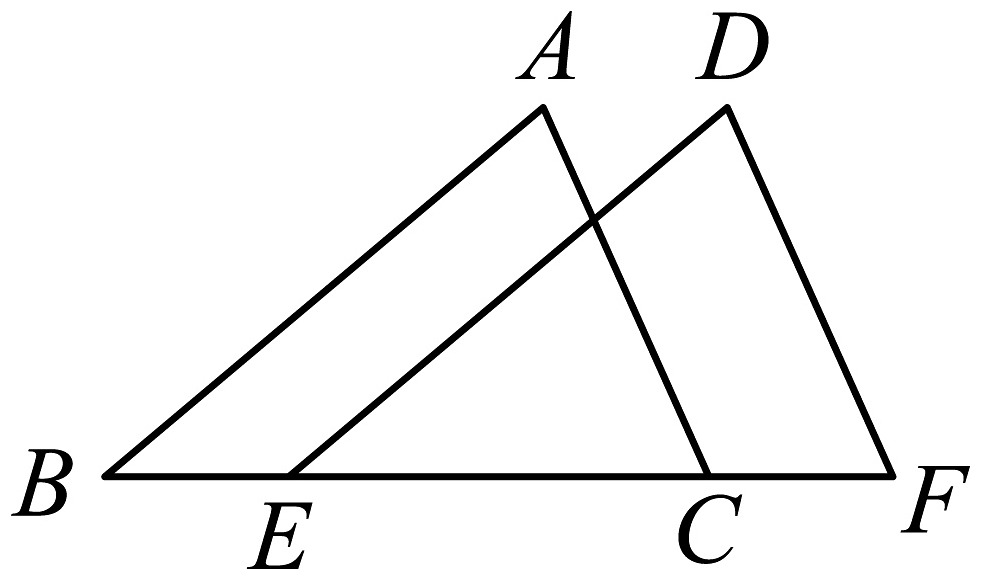 A、 B、 C、 D、6. 如图, , .
A、 B、 C、 D、6. 如图, , .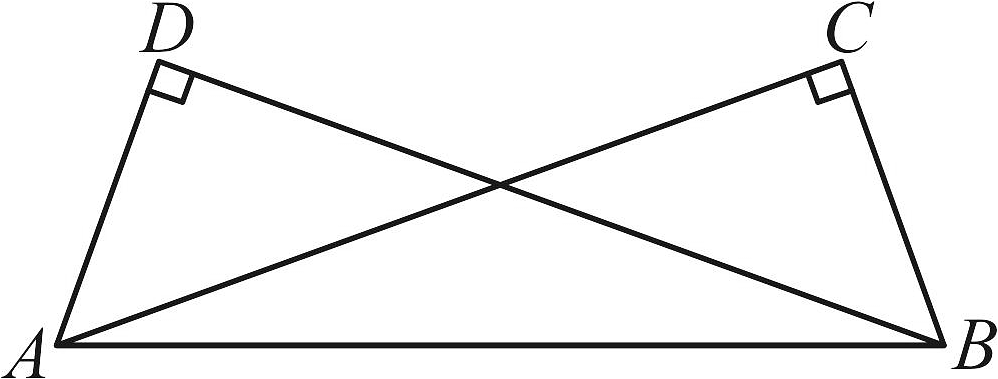 (1)、求证:;(2)、若 , 则__________°.7. 如图,四边形中,于点F,交于点E,连接 , 平分 .
(1)、求证:;(2)、若 , 则__________°.7. 如图,四边形中,于点F,交于点E,连接 , 平分 . (1)、求证:;(2)、若 , 求的长.8. 下面是多媒体上的一道习题:
(1)、求证:;(2)、若 , 求的长.8. 下面是多媒体上的一道习题:如图是的中线, , 求的取值范围.

请将下面的解题过程补充完整.
解:延长至点E,使 , 连接 .
∵是的中线,
∴ ,
在和中,
,
∴( ),
∴ ,
在中,根据“三角形三边关系”可知:_____________________,
又∵ ,
∴______________________.

二、能力提高
-
9. 如图,在中, , , 为射线上一动点,连结 , 将绕点顺时针旋转至交直线于点 , 若 , 则 .
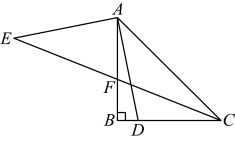 10. 如图,在中,是中线,过点作于点 , 过点作交BF的延长线于点 . 下列结论:①;②;③;④;⑤ . 正确的个数是( )
10. 如图,在中,是中线,过点作于点 , 过点作交BF的延长线于点 . 下列结论:①;②;③;④;⑤ . 正确的个数是( )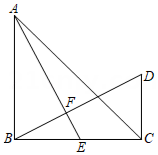 A、2个 B、3个 C、4个 D、5个11. 如图所示,在平面直角坐标系中,
A、2个 B、3个 C、4个 D、5个11. 如图所示,在平面直角坐标系中, (1)、点A在x的正半轴运动,点B在y的正半轴上,且 ,
(1)、点A在x的正半轴运动,点B在y的正半轴上,且 ,①求证::
②求的值;
(2)、点A在x的正半轴运动,点B在y的负半轴上,且 , 求的值.12. (1)、如图1,在中, , , 是边上的中线,延长到点使 , 连结 , 把 , , 集中在中,利用三角形三边关系可得的取值范围。请写出的取值范围,并说明理由(2)、如图2,在中,是边上的中线,点 , 分别在 , 上,且 , 求证:。小艾同学受到(1)的启发,在解决(2)的问题时,延长到点 , 使……,请你帮她完成证明过程。(3)、如图3,在四边形中,为钝角,为锐角, , , , 点 , 分别在 , 上,且 , 连结 , 试探索线段 , , 之间的数量关系,并加以证明.13. 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)、如图1,在中, , , 是边上的中线,延长到点使 , 连结 , 把 , , 集中在中,利用三角形三边关系可得的取值范围。请写出的取值范围,并说明理由(2)、如图2,在中,是边上的中线,点 , 分别在 , 上,且 , 求证:。小艾同学受到(1)的启发,在解决(2)的问题时,延长到点 , 使……,请你帮她完成证明过程。(3)、如图3,在四边形中,为钝角,为锐角, , , , 点 , 分别在 , 上,且 , 连结 , 试探索线段 , , 之间的数量关系,并加以证明.13. 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)、【感知】当直线MN绕点C旋转到图①的位置时,易证△ADC≌△CEB(不需要证明),进而得到DE、AD、BE之间的数量关系为 .
(2)、【探究】当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE.
(3)、当直线MN绕点C旋转到图③的位置时,直接写出DE、AD、BE之间的数量关系.14. 有两个三角形,分别为△ABC和△ADE,其中∠CAB=∠DAE=90°,AB=AC,AD=AE. (1)、若按如图(1)所示位置摆放,使得AC与AD重合,连接BD,CE,则BD与CE的数量关系是;(2)、在图(2)中,延长BD交CE于点F,求∠BFC的度数;(3)、若按如图(3)所示位置摆放,连接BD,CE,且BD与CE交于点F,BD与AC交于点H,请判断BD与CE之间的关系,并说明理由.15. 如图,一次函数的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)、若按如图(1)所示位置摆放,使得AC与AD重合,连接BD,CE,则BD与CE的数量关系是;(2)、在图(2)中,延长BD交CE于点F,求∠BFC的度数;(3)、若按如图(3)所示位置摆放,连接BD,CE,且BD与CE交于点F,BD与AC交于点H,请判断BD与CE之间的关系,并说明理由.15. 如图,一次函数的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°. (1)、求C点坐标;(2)、求过B、C两点直线的解析式;(3)、在坐标平面内求一点D,使△ABD与△ABC全等.直接写出所有点D的坐标;(4)、在y轴上求一点P,使△APB的面积与△ABC的面积相等.直接写出所有点P的坐标.16. 如图,点A,E,F,C在一条直线上, , . 过点E,F分别作 , , 点B,D分别在直线两侧, . 连接 , 与直线交于点G.
(1)、求C点坐标;(2)、求过B、C两点直线的解析式;(3)、在坐标平面内求一点D,使△ABD与△ABC全等.直接写出所有点D的坐标;(4)、在y轴上求一点P,使△APB的面积与△ABC的面积相等.直接写出所有点P的坐标.16. 如图,点A,E,F,C在一条直线上, , . 过点E,F分别作 , , 点B,D分别在直线两侧, . 连接 , 与直线交于点G. (1)、求证: , .(2)、若 , , 直接写出的长度 .(3)、若保持不动,将的边沿直线方向移动,其余条件不变,请你画出图形,并直接写出的长度(用m、n表示)
(1)、求证: , .(2)、若 , , 直接写出的长度 .(3)、若保持不动,将的边沿直线方向移动,其余条件不变,请你画出图形,并直接写出的长度(用m、n表示)三、拓展创新
-
17. 在平面中,对于点M,N,P,若 , 且 , 则称点P是点M和点N的“垂等点”.

在平面直角坐标系中,
(1)、已知点 , 点 , 则点中是点M和点N的“垂等点”的是___________;(2)、已知点 .①若在第二象限内存在点C,使得点B是点A和点C的“垂等点”,写出点C的坐标(用含b的式子表示),并说明理由;
②当时,点D,点E是线段AO,BO上的动点(点D,点E不与点A,B,O重合).若点F是点D和点E的“垂等点”,直接写出点F的纵坐标t的取值范围.