湘教版（2024）数学七年级上册 1.7 有理数的混合运算同步分层练习

试卷更新日期：2025-08-18 类型：同步测试

进入出卷网下载

一、夯实基础

1. 小明和小红利用温差测量山峰的高度．小明在山顶测得温度是 $- 1 ° C$ ，小红此时在山脚测得温度是 $11 ° C$ ，已知该地区高度每增加100米，气温大约下降 $0.8 ° C$ ，则这个山峰的高度大约是（）

A、800米 B、1250米 C、1200米 D、1500米

查看试题解析
2. 用2，0，2，4这四个数进行如下运算，计算结果最大的式子为（）

A、2-0×2+4 B、2-0+2×4 C、2×0+2-4 D、2+0-2×4

查看试题解析
3. 下列计算正确的是（）

A、 $\frac{1}{3} - \frac{1}{3}$ ×4=0×4=0 B、4÷（-2）×（ $- \frac{1}{2}$ ）=4÷1=4 C、-3²-（-2）³=9-8=1 D、 $(- \frac{1}{4}) \div (\frac{1}{12} + \frac{1}{16}) = (- \frac{1}{4}) \div \frac{7}{48} = - \frac{12}{7}$

查看试题解析
4. 在数学课上，老师让甲、乙、丙、丁四位同学分别做了一道有理数计算题，你认为做对的同学是（）
甲： $12 - (2 \times 3^{2}) = 12 - 2 \times 6 = 0$ ；乙： $(36 - 12) \div \frac{4}{3} = 36 \times \frac{3}{4} - 12 \times \frac{3}{4} = 18$
丙： $(- 3)^{2} \div \frac{3}{4} \times 4 = 9 \div 3 = 3$ ；丁： $9 - 3^{2} \div 4 = 0 \div 4 = 0$

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 规定运算： $a \otimes b = a^{2} + a b - 5,$ 例如 $1 \otimes 1 = 1^{2} + 1 \times 1 - 5 .$ .则（-3）⊗6的值为（）

A、-14 B、-32 C、-17 D、-8

查看试题解析
6. 如图，小明设计了一个运算程序，若输入数值为-5，则输出的结果为（）

A、 $- 24$ B、 $- 21$ C、24 D、56

查看试题解析
7. 老师设计了计算接力游戏，规则是每名同学只能利用前面一个同学的式子，进一步计算，将计算的结果传给下一个同学，最后解决问题．过程如下：
其中步骤错误的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 下列计算：① 0－(－3)＝0＋(－3)＝－3；②7－3×4＝7－12＝－5；③4÷3×(－ $\frac{1}{3}$ )＝4÷(－1)＝－4；④－1²－2×(－1)²＝－1－2＝－3.
其中正确的是.(填序号)

查看试题解析
9. 在山顶测的温度是-4℃，在山脚测的温度是2℃，已知山峰高度每增加100米，气温大约下降0.6℃，这座山峰的高度大约是米.

查看试题解析
10. 有这样一个数字游戏，用 $1$ ， $- 5$ ， $11$ ， $a$ 四个数通过加、减、乘、除四则运算，可以得到结果 $24$ ．若 $a$ 是绝对值不大于 $5$ 的整数，请写出一个满足条件的算式：．

查看试题解析
11. 一个数值转换机如下所示．若输入数为2，则输出数是

查看试题解析
12. 计算
⑴ $3 + 50 \div 2^{2} \times (- \frac{1}{5}) - 1$
=3+50÷ $\times (- \frac{1}{5}) - 1$ ……先算乘方
=3+-1……再算乘除
=；……最后算加减
⑵ $- 2^{4} + | 6 - 10 | - 3 \times (- 1)^{2024}$
=+-3×……先算乘方和绝对值
=+-……再算乘法
=.……最后算加减

查看试题解析
13. 计算：

(1)、 $| - 8 | \div \frac{4}{9} \times {(- \frac{1}{2})}^{3}$

(2)、 $- 3^{2} - (1 - 0.5) \times \frac{1}{2} \times [5 - {(- 3)}^{2}]$

查看试题解析

二、能力提升

14. 当温度每上升 $1 ℃$ 时，某种金属丝伸长 $0.002 mm$ ；反之，当温度下降 $1 ℃$ 时，金属丝就缩短 $0.002 mm$ ．把 $15 ℃$ 的这种金属丝加热到 $60 ℃$ ，再使它冷却降温到 $5 ℃$ ．金属丝最后的长度比原来的长度伸长（） $mm$ ．

A、 $0.02$ B、 $- 0.02$ C、 $0.09$ D、 $- 0.11$

查看试题解析
15. 若 $a$ 是最大的负整数， $b$ 是绝对值最小的有理数， $c$ 是倒数等于它本身的自然数，则 $a^{2022} + 2021 b + c^{2022}$ 的值为（）

A、2 B、0 C、2021 D、2022

查看试题解析
16. 在数学课上，老师让甲、乙、丙、丁四位同学分别做了一道有理数计算题，你认为做对的同学是 ( )
甲： $64 - 2^{2} \div 60 = 1 .$
乙： $24 - 4 \times 3^{2} = 24 - 4 \times 6 = 0 .$
丙： ${(- 3)}^{2} \div \frac{1}{3} \times 3 = 9 \div 1 = 9 .$
丁： $(36 - 12) \div \frac{3}{2} = 36 \times \frac{2}{3} - 12 \times \frac{2}{3} = 16 .$

A、甲 B、乙 C、丙 D、丁

查看试题解析
17. 下列运算中，错误的是 ( )

A、-5×(-4)×(-3)×2=-120 B、 $- 24 \times (- \frac{3}{4} + \frac{1}{6} + \frac{2}{3}) = 18 - 4 - 16 = - 2$ C、 $(- 14) \times (- 6) \times (+ \frac{2}{7}) \times (- \frac{2}{3}) = 16$ D、(-2)×(+7)-(-2)×3-2×(-4)=-2×(7-3-4)=0

查看试题解析
18. 定义一种新运算“ $\otimes$ ”，规定： $a \otimes b = 2 a - 3 b$ 等式右边的运算就是加、减、乘、除四则运算，例如： $2 \otimes (- 3) = 2 \times 2 - 3 \times (- 3) = 4 + 9 = 13$ ， $1 \otimes 2 = 2 \times 1 - 3 \times 2 = 2 - 6 = - 4$ ．则 $(- 1) \otimes [3 \otimes (- 2)]$ 的值是（）．

A、 $- 2$ B、 $- 18$ C、 $- 28$ D、 $- 38$

查看试题解析
19. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．一位书生坚持每天五更起床读书，为了勉励自己，他用“结绳计数”的方法来记录自己读书的天数，如图1是他从右到左依次排列的绳子上打结，满六进一，表示的天数为51天（1×6²+2×6+3＝51），按同样的方法，图2表示的天数是（　　）

A、48 B、46 C、236 D、92

查看试题解析
20. $\frac{(- 1)^{n} - (- 1)^{n + 1}}{2}$ （ $n$ 为正整数）的值为（）

A、 $- 1$ 或0 B、0或1 C、 $- 1$ 或1 D、 $- 1$ 或0或1

查看试题解析
21. 有个填写运算符号的游戏：在“2□3□6-5”中的每个□内，填入+，-，×，÷中的某一个(可重复使用)，然后计算结果，则计算所得结果的最小值为（）

A、-23 B、-21 C、-12 D、-5

查看试题解析
22. 计算 ${(- 4)}^{2} \times (- 0.25) \times (1.25)$ 的结果为。

查看试题解析
23. 已知长为300米的秋游队伍，以2米/秒的速度向东行进，在队尾处的甲有一物品要送到队头，送到后立即返回队尾.若甲的往返速度均为4米/秒，则甲往返共用的时间为秒.

查看试题解析
24. 有理数a，b，c在数轴上的位置如下图所示，则下列结论中正确的是(填序号)

①a+b+c<0；②abc<0；③(a-b) ÷c<0；④ $\frac{1}{a} - \frac{1}{b}$ <0

查看试题解析
25. 如图所示的运算程序：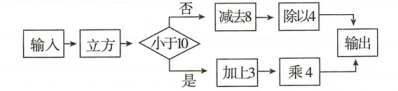
若输入值为-2，则输出的值为.

查看试题解析
26. 计算.

(1)、 $(\frac{1}{2} - \frac{5}{9} + \frac{7}{12}) \times (- 36)$ ；

(2)、 $[2 - 5 \times {(- \frac{1}{2})}^{2}] \div (- \frac{1}{4})$

(3)、 $1 \frac{1}{2} \times \frac{5}{7} - (- \frac{5}{7}) \times 2 \frac{1}{2} + (- \frac{1}{2}) \div 1 \frac{2}{5}$

(4)、 $- 1^{4} - [1 - (1 - 0.5 \times \frac{1}{3}) \times 6]$

查看试题解析

三、拓展创新

27. 定义运算“ $*$ ”：对于任意有理数a和b，规定 $a * b = b^{2} - a b - 3$ ，如 $2 * 3 = 3^{2} - 2 \times 3 - 3 = 0$ .

(1)、求 $- 5 * (- 3)$ 的值；

(2)、若 $(a - 3) * (- \frac{3}{4}) = a - 1$ ，求a的值.

查看试题解析
28. 观察算式：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2} = \frac{1}{2}$ ；
$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} = \frac{2}{3}$ ；
$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} = \frac{3}{4}$ ；

(1)、按规律填空：
① $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} =$ ________；
②如果 $n$ 为正整数，那么 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} + \cdot \cdot \cdot + \frac{1}{n \times (n + 1)} =$ ________；

(2)、计算（由此拓展写出具体过程） $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \cdot \cdot \cdot + \frac{1}{99 \times 101}$ ；

查看试题解析

29. 根据以下素材，尝试解决问题.

如何获得更高的销售额?
素材1	甲菜农有6筐蔬菜，每筐质量在20千克左右，他将超过20千克的千克数记为正数，不足的千克数记为负数，记录如图.超过20千克的他以170元/筐的价格售出，其余三筐他以9元/千克销售，并全部售出.
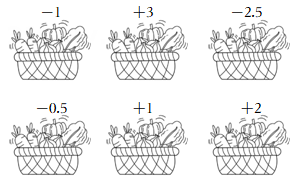
素材2	乙菜农将蔬菜堆放在一起进行销售，售出蔬菜的质量比甲菜农少20千克，其中80千克以10 元/千克销售，剩下的部分按八折全部售出.
问题解决
问题1	(1)求甲菜农售出最重的一筐蔬菜的质量.
问题2	(2)求乙菜农售出的蔬菜的总质量.
问题3	(3)甲、乙菜农的蔬菜全部售出后，哪一位菜农的销售额更高? 高多少元?

查看试题解析

湘教版（2024）数学七年级上册 1.7 有理数的混合运算 同步分层练习

一、夯实基础

二、能力提升

三、拓展创新

湘教版（2024）数学七年级上册 1.7 有理数的混合运算同步分层练习