浙教版(2024) 数学八年级上册1.5.5 三角形全等的判定(综合) 同步分层练习
试卷更新日期:2025-08-18 类型:同步测试
一、夯实基础:
-
1. 如图所示,一扇窗户打开后,用窗钩 AB 即可固定,这里所用的几何原理是( )
 A、两点之间线段最短 B、垂线段最短 C、三角形具有稳定性 D、两点确定一条直线2. 如图,已知 , 添加下列条件还不能判定的是( )
A、两点之间线段最短 B、垂线段最短 C、三角形具有稳定性 D、两点确定一条直线2. 如图,已知 , 添加下列条件还不能判定的是( ) A、 B、 C、 D、3. 如图, , , 添加下列哪一个条件可以推证≌( )
A、 B、 C、 D、3. 如图, , , 添加下列哪一个条件可以推证≌( ) A、 B、 C、AC∥DF D、4. 如图所示,某工程队欲测量山脚两端A、B间的距离,在山旁的开阔地取一点C,连接AC、BC并分别延长至点D,点E,使得CD=AC,CE=BC,测得DE的长,就是AB的长,那么判定△ABC≌△DEC的理由是( )
A、 B、 C、AC∥DF D、4. 如图所示,某工程队欲测量山脚两端A、B间的距离,在山旁的开阔地取一点C,连接AC、BC并分别延长至点D,点E,使得CD=AC,CE=BC,测得DE的长,就是AB的长,那么判定△ABC≌△DEC的理由是( ) A、SSS B、SAS C、ASA D、AAS5. 如图,中边上的高为 , 中边上的高为 . 若 , 下列结论中正确的是( )
A、SSS B、SAS C、ASA D、AAS5. 如图,中边上的高为 , 中边上的高为 . 若 , 下列结论中正确的是( ) A、 B、 C、 D、无法确定6. 如图,点 是 的中点,要使 ,还需要添加一个条件可以是(只需写出一种情况)
A、 B、 C、 D、无法确定6. 如图,点 是 的中点,要使 ,还需要添加一个条件可以是(只需写出一种情况)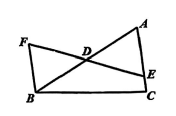 7. 已知如图: , 且 , 于 , 于 , , .连结 , .则图中阴影部分的面积为.
7. 已知如图: , 且 , 于 , 于 , , .连结 , .则图中阴影部分的面积为.
二、能力提升:
-
8. 如图,已知 , , 且 , 那么是的 . (填“中线”或“角平分线”)
 9. 如图,点D在内部,平分 , 且 , 连接 . 若的面积为2,则的面积为 .
9. 如图,点D在内部,平分 , 且 , 连接 . 若的面积为2,则的面积为 . 10. 等腰Rt△ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E , 交BA的延长线于F , 若AB=8,则△FBC的面积为
10. 等腰Rt△ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E , 交BA的延长线于F , 若AB=8,则△FBC的面积为 11. 如图1,于点于点B,P,Q分别为线段AB,BD上任意一点.
11. 如图1,于点于点B,P,Q分别为线段AB,BD上任意一点. (1)、如图1,若 , 求AC,BQ,AB之间的数量关系;(2)、如图2,""改为"(为锐角)".若 , , 判断(1)中的数量关系是否会改变?并说明理由.12. 如图,在中,D为上一点,E为中点,连接并延长至点F,使得 , 连 .
(1)、如图1,若 , 求AC,BQ,AB之间的数量关系;(2)、如图2,""改为"(为锐角)".若 , , 判断(1)中的数量关系是否会改变?并说明理由.12. 如图,在中,D为上一点,E为中点,连接并延长至点F,使得 , 连 . (1)、求证:(2)、若 , 求的度数.13. 如图,中, , D是BA延长线上一点,点E是∠CAD的平分线上一点,过点E作EF⊥AC于F , EG⊥AD于G .
(1)、求证:(2)、若 , 求的度数.13. 如图,中, , D是BA延长线上一点,点E是∠CAD的平分线上一点,过点E作EF⊥AC于F , EG⊥AD于G . (1)、求证:;(2)、若 , , , 求AF的长.14. 将两个三角形纸板和按如图所示的方式摆放,连接DC . 已知 , , .
(1)、求证:;(2)、若 , , , 求AF的长.14. 将两个三角形纸板和按如图所示的方式摆放,连接DC . 已知 , , . (1)、试说明:;(2)、若 , 求的度数.
(1)、试说明:;(2)、若 , 求的度数.三、拓展创新:
-
15.
 (1)、如图1,在中, , , 是边上的中线,延长到点使 , 连结 , 把 , , 集中在中,利用三角形三边关系可得的取值范围。请写出的取值范围,并说明理由(2)、如图2,在中,是边上的中线,点 , 分别在 , 上,且 , 求证:。小艾同学受到(1)的启发,在解决(2)的问题时,延长到点 , 使……,请你帮她完成证明过程。(3)、如图3,在四边形中,为钝角,为锐角, , , , 点 , 分别在 , 上,且 , 连结 , 试探索线段 , , 之间的数量关系,并加以证明.
(1)、如图1,在中, , , 是边上的中线,延长到点使 , 连结 , 把 , , 集中在中,利用三角形三边关系可得的取值范围。请写出的取值范围,并说明理由(2)、如图2,在中,是边上的中线,点 , 分别在 , 上,且 , 求证:。小艾同学受到(1)的启发,在解决(2)的问题时,延长到点 , 使……,请你帮她完成证明过程。(3)、如图3,在四边形中,为钝角,为锐角, , , , 点 , 分别在 , 上,且 , 连结 , 试探索线段 , , 之间的数量关系,并加以证明.