浙教版（2024) 数学八年级上册1.4 全等三角形同步分层练习

试卷更新日期：2025-08-17 类型：同步测试

进入出卷网下载

1. 如图，若两个三角形全等，图中字母表示三角形边长，则 $∠ 1$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
2. 如图，点 $B$ 、 $C$ 、 $D$ 在同一直线上，若 $△ A B C ≌ △ C D E$ ， $D E = 4$ ， $B D = 13$ ，则 $A B$ 等于（）

A、 $7$ B、 $8$ C、 $9$ D、 $10$

查看试题解析
3. 一个三角形的三边为3，5，x，另一个三角形的三边为y，3，6，如果这两个三角形全等，那么x+y=.

查看试题解析
4. 如图，将图形沿直线AC对折，△ABC与△ADC重合，则△ABC≌.AB的对应边是， BC的对应边是∠BCA的对应角是：

查看试题解析

5. 若△ABC≌△DEF ，且△ABC的周长为15，AB＝5，BC＝4，则DF的长为（　　）

A、4或5 B、5 C、4 D、6

查看试题解析
6. 如图， $△ A B C ≌ △ A^{'} B^{'} C^{'}$ ，边 $B^{'} C^{'}$ 过点A且平分 $∠ B A C$ 交 $B C$ 于点D， $∠ B = 24 °$ ， $∠ C D B^{'} = 96 °$ ，则 $∠ C^{'}$ 的度数为（）

A、24 ° B、36 ° C、45 ° D、60 °

查看试题解析
7. 如图，在锐角 $△ A B C$ 中，D，E分别是 $A B ， A C$ 边上的点， $△ A D C ≌ △ A D C^{'}$ ， $△ A E B ≌ △ A E B^{'}$ ，且 $C^{'} D ∥ E B^{'} ∥ B C$ ， $B E 、 C D$ 交于点F．若 $∠ B A C = 40 °$ ，则 $∠ B F C =$ （）

A、 $80 °$ B、 $90 °$ C、 $100 °$ D、无法确定

查看试题解析
8. 如图，已知△ACF≌△DBE，∠E=∠F，AD=15cm，BC=9cm，则AB的长为cm.

查看试题解析
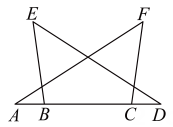9. 如图所示，已知△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD，垂足为F，若∠BCE=65°，求∠CAF的度数.

查看试题解析
10. 如图，已知 $△ A B C ≌ △ D E F$ ，点 $B, E, C, F$ 在同一直线上．

(1)、若 $∠ A = 95 °$ ， $∠ F = 55 °$ ，求 $∠ D E F$ 的度数；

(2)、若 $B C = 6$ ，点 $E$ 是 $B C$ 的中点，求 $C F$ 的长．

查看试题解析

浙教版（2024) 数学八年级上册1.4 全等三角形 同步分层练习