浙教版（2024) 数学八年级上册1.5.1三角形全等的判定一(sss) 同步分层练习
试卷更新日期：2025-08-17 类型：同步测试
一、夯实基础：
-
1. 下列图形中，具有稳定性的是（ ）A、
B、
C、
D、
2. 如图所示，一扇窗户打开后，用窗钩 AB 即可固定，这里所用的几何原理是（ ）
A、两点之间线段最短 B、垂线段最短 C、三角形具有稳定性 D、两点确定一条直线3. 如图，周师傅用4根木条钉成一个四边形木架，要使这个木架不变形，他至少要再钉上木条的根数是( ).
A、1根 B、2根 C、3根 D、4根4. 如图，在边长为1的正方形网格图中标有A，B，C，D，E，F六个格点.根据图中标示的各点位置，与△ABC全等的是( ).
A、△ACF B、△ACE C、△BAD D、△CEF5. 如图，作的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于、 ， 再分别以点C、D为圆心，以大于长为半径画弧，两弧交于点P ， 作射线OP由作法得的根据是（ ）
A、SAS B、ASA C、AAS D、SSS6. 如图，已知点A，D，C，F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，依据“SSS"还需要添加的一个条件是（ ）
A、AD=CD B、AD=CF C、BC∥EF D、DC=CF7. 如图，在△ABC和△BAD中，BC=AD，请你再补充一个条件，使△ABC≌△BAD(SSS)．你补充的条件是.
8. 周末小高同学全家去饭店吃饭，他发现饭店房间里放着一个儿童座椅（如图），他观察这个儿童座椅的主体框架成三角形，从而保证儿童坐上去会很安全，这样的设计利用的数学原理是三角形的（填“稳定性”或“不稳定性”）．
9. 已知：如图，在四边形ABCD中，AB=CD，AD=CB.求证：∠1=∠2.
将下面的证明过程和理由补充完整.
证明：在△ABD与△CDB中，
∴△ABD≌△CDB( )；.
∴∠1=∠2( ).
二、能力提升：
-
10. 油纸伞是汉族古老的传统用品之一.图1是一把油纸伞实物图，图2 为其伞骨示意图.已知 那么△AED ≌△AFD 的依据是( )
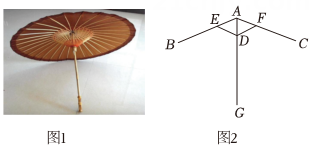A、SSS B、ASA C、AAS D、SAS11. 如图，已知与上的点C，点A，小临同学现进行如下操作：①以点O为圆心，长为半径画弧，交于点D，连接；②以点A为圆心，长为半径画弧，交于点M；③以点M为圆心，长为半径画弧，交第2步中所画的弧于点E，连接 ． 下列结论不能由上述操作结果得出的是（ ）
A、 B、 C、 D、12. 工人师傅常用角尺来平分一个任意角.作法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点P的射线OP即是∠AOB的平分线.这种作法的道理是.
13. 如图，点B、C、E三点在同一直线上，且AB＝AD，AC＝AE，BC＝DE，若 ， 则∠3＝°．
14. 如图，点 在一条直线上， ．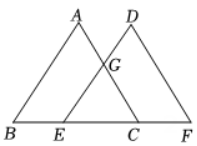
(1)、求证： ；(2)、若 ，求 的大小．
