浙教版（2024) 数学八年级上册1.5.2三角形全等的判定二(SAS) 同步分层练习

试卷更新日期：2025-08-17 类型：同步测试

进入出卷网下载

一、夯实基础：

1. 如图所示，BC交AD于点O，OA=OB，OC=OD，∠D=30°，∠A=90°，则∠B的度数为( )

A、30° B、90° C、120° D、60°

查看试题解析
2. 下列表格中，填入“◎”处正确的是（）
已知： $A B ⊥ B E, D E ⊥ B E$ ，且 $B F = C E, A B = D E$ ．
求证： $△ A B C ≌ △ D E F$
证明： $∵ A B ⊥ B E, D E ⊥ B E$
$∴ ∠ B = ∠ E = 90 °$
又 $∵ B F = C E, A B = D E$ ，
∴ $B C = E F$
$∴ △ A B C ≅ △ D E F$ （◎）

A、 $AAS$ B、 $SSS$ C、 $ASA$ D、 $SAS$

查看试题解析
3. 如图，要用“SAS”证 $△ A B C ≌ △ A D E$ ，若已知 $A B = A D$ ， $B C = D E$ ，则还需条件（）

A、 $∠ B = ∠ D$ B、 $∠ C = ∠ E$ C、 $∠ 1 = ∠ 2$ D、 $∠ 3= ∠ 4$

查看试题解析
4. 如图，把两根钢条 $A A^{'}$ ， $B B^{'}$ 的中点连在一起，可以做成一个测量工件内槽宽的卡钳．若求 $A B$ 的长，只需测量下列线段中的（）

A、 $A^{'} B^{'}$ B、 $O A^{'}$ C、 $O B^{'}$ D、OA

查看试题解析
5. 如图， $△ C D E$ 的顶点 $E$ 在 $△ A B C$ 的边 $B C$ 上，且 $C E = A C$ ， $B C = D E$ ， $∠ A C B = ∠ C E D = 90 °$ ，则下列说法不正确的是（）

A、 $△ A B C$ ≌ $△ C D E$ B、 $∠ B = ∠ D$ C、 $A C / / D E$ D、 $B E = C E$

查看试题解析
6. 如图，小明与小敏玩跷跷板游戏，如果跷跷板的支点 $O$ （即跷跷板的中点）至地面的距离是 $45 cm$ ，当小敏从水平位置 $C D$ 下降 $20 cm$ 时，小明离地面的高度是（）

A、 $20 cm$ B、 $45 cm$ C、 $25 cm$ D、 $65 cm$

查看试题解析
7. 如图所示， $A A^{'}$ ， $B B^{'}$ 表示两根长度相同的木条，若 $O$ 是 $A A^{'}$ ， $B B^{'}$ 的中点，经测量 $A B = 9 c m$ ，则容器的内径 $A^{'} B^{'}$ 为 $c m$ ．

查看试题解析
8. 如图，点B，F，E，C在同一直线上， $A B ∥ C D$ ，且 $A B = C D$ ，要使 $△ A B E ≌ △ D C F$ ，则可以添加的条件是．（只需填上一个即可）

查看试题解析
9. 如图，点C是线段 $A B$ 的中点， $A D = B E$ ， $∠ A = ∠ B$ ．求证： $∠ D = ∠ E$ ．

查看试题解析
10. 如图，点 $D$ 在 $A B$ 上，点 $E$ 在 $A C$ 上， $A B = A C$ ， $B D = C E$ ，求证： $∠ B = ∠ C$ ．

查看试题解析

二、能力提升：

11. 数学活动课上，小星制作了一个燕尾形的风筝 $.$ 如图， $A D = C D$ ， $∠ A D B = ∠ C D B$ ，他准备用刻度尺量 $A B$ 和 $B C$ 的长是否相等．
小英却说：“不用再测量，因为 $△ A B D$ ≌ $△ C B D$ ，所以 $A B = B C .$ ”
小英用到的判定三角形全等的方法是（）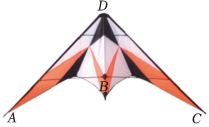

A、 $S A S$ B、 $A A S$ C、 $S S S$ D、 $A S A$

查看试题解析
12. 如图，为测量池塘两端A、B的距离，小康在池塘外一块平地上选取了一点O ，连接AO ， BO ，并分别延长AO ， BO到点C ， D ，使得AO＝DO ， BO＝CO ，连接CD ，测得CD的长为165米，则池塘两端A ， B之间的距离为（）

A、160米 B、165米 C、170米 D、175米

查看试题解析
13. 如图， $A D$ 是 $△ A B C$ 的中线，E，F分别是 $A D$ 和 $A D$ 延长线上的点，且 $D E = D F$ ，连接 $B F$ ， $C E$ ，下列说法：① $△ A B D$ 和 $△ A C D$ 面积相等；② $∠ B A D = ∠ C A D$ ；③ $△ B D F ≅ △ C D E$ ；④ $B F ∥ C E$ ；⑤ $C E = A E$ ．其中正确的是（　　）

A、①② B、③⑤ C、①③④ D、①④⑤

查看试题解析
14. 如图，在△ABC中，按以下步骤作图：①以点C为圆心，任意长为半径作弧，分别交AC，CB于点E和F；②分别以E，F为圆心，大于 $\frac{1}{2}$ EF为半径画弧，两弧交于点D；③作射线CD交AB于点G；延长CA至H，使CH＝CB，连接HG，若AH＝2，AB＝5，则△AHG的周长为 .

查看试题解析
15. 如图，AE=AC，BC=DE，若添加一个条件可得△ABC≌△ADE，则添加的条件可以是.（写出一个满足条件的答案）

查看试题解析
16. 如图，已知 $A B = A C, A D = A E, ∠ B A C = ∠ D A E, A B$ 和 $C D$ 交于点 $F$ ，若点 $C 、 E$ 、 $F 、 D$ 共线， $S_{△ A C F} = 9, S_{△ B D F} = 4$ 时，则 $S_{△ A D E} =$ ．

查看试题解析
17. 八 $(1)$ 班数学兴趣活动小组的同学们利用课余时间制作了圆柱形容器内径测量仪，如图 $.$ 制作和使用方法：将两根等长的木棒中心固定在一起，两根木棒可以绕固定点 $O$ 自由旋转 $.$ 测量圆柱形容器内径时，把测量仪的一端放入容器内，再将木棒的两端张开，只要测出露在外面的一端两个木棒之间的距离 $A D$ ，就知道了容器的内径 $C B$ 的大小 $.$ 请你用学过的数学知识解释测量仪的工作原理 $($ 写出已知、求证，并证明 $)$ ．
已知：如图，线段 $A B$ 、 $C D$ 相交于点 $O$ ， ▲ ，连结 $A D$ 、 $B C$ ．
求证：
证明：

查看试题解析

三、拓展创新：

18. 如图，已知 $B D$ 为 $△ A B C$ 的角平分线，延长 $B D$ 到 $E$ ，使得 $E D = A D$ ，连接 $E C$ ，若 $B C = A B + E C$ ，且 $∠ A = α (70 ° \leq α \leq 100 °)$ ．

(1)、求证： $C D$ 平分 $∠ B C E$ ；

(2)、求 $∠ E$ 的取值范围；

(3)、若延长 $B A$ ， $C E$ 相交于点 $H$ ，求 $∠ H$ 的度数．

查看试题解析