2.2《平方根与立方根》（2）—北师大版数学八年级上册课堂分层训练

试卷更新日期：2025-08-14 类型：同步测试

进入出卷网下载

一、基础应用

1. 4的平方根是（）

A、 $\sqrt{2}$ B、－ $\sqrt{2}$ C、±4 D、±2

查看试题解析
2. $\sqrt{81}$ 的平方根是（）

A、9 B、±9 C、±3 D、3

查看试题解析
3. 下列运算正确的是（）

A、 $- \sqrt{{(- 7)}^{2}} = 7$ B、 $\sqrt{{(- 6)}^{2}} = - 6$ C、 $- \sqrt{25} = - 5$ D、 $\sqrt{9} = \pm 3$

查看试题解析
4. 下列说法正确的是（）
①负数没有平方根；②一个实数的立方根不是正数就是负数；③任何数的平方都是非负数，因此任何数的平方根也是非负数；④任何一个非负数的平方根都不大于这个数；⑤平方根等于它本身的数是0

A、①② B、③⑤ C、②④ D、①⑤

查看试题解析
5. 下列说法正确的是（）

A、9的平方根是3 B、36的算术平方根是6 C、 $\sqrt{49}$ 的平方根是 $\pm 7$ D、 $- 25$ 的算术平方根是5

查看试题解析
6. 已知某正实数的平方根是 $a + 2$ 和 $7 - 2 a$ ，那么这个正实数是．

查看试题解析
7. $\sqrt{16} =$ ； $\sqrt{81}$ 的平方根是.

查看试题解析
8. $\frac{4}{9}$ 的平方根是； $\sqrt{16}$ 的算术平方根是．

查看试题解析

二、能力提升

9. 实数 $1 - 3 a$ 有平方根，则 $a$ 可以取的值为（）

A、0 B、1 C、2 D、3

查看试题解析
10. 下列说法正确的是( )

A、 $1$ 的平方根与算术平方根都是 $1$ B、 $- 4$ 的算术平方根是 $2$ C、 $\sqrt{16}$ 的平方根是 $\pm 4$ D、 $4$ 的平方根是 $\pm 2$

查看试题解析
11. 下列判断中，错误的是（　　）

A、 $- 1$ 的平方根是 $\pm 1$ B、 $- 1$ 的倒数是 $- 1$ C、 $- 1$ 的绝对值是1 D、 $- 1$ 的平方的相反数是 $- 1$

查看试题解析
12. 某正数的平方根分别是 $2 a + 1$ 和 $a + 5$ ，则 $a =$ ．

查看试题解析
13. 阅读，一般地，如果一个数 $x$ 的平方等于 $a$ ，即 $x^{2} = a$ ，那么这个数 $x$ 就叫做 $a$ 的平方根（也叫做二次方根）．如： ${(- 2)}^{2} = 4$ ， $2^{2} = 4$ ，所以 $- 2$ 和2叫做4的平方根，4的平方根记为 $\pm \sqrt{4}$ ， $\pm \sqrt{4} = \pm 2$ ，又如：若 $x^{2} = 2$ ，则2的平方根是： $\pm \sqrt{2}$ ，填空：25的平方根是， $\frac{49}{121}$ 的平方根是， 5的平方根是．

查看试题解析
14. 如图，长方形内有2个相邻的正方形，面积分别为9和 $x^{2}$ ，那么阴影部分的面积为．

查看试题解析
15. 有一个数值转换器，原理如图所示，当输入的数为16时，输出的数为．

查看试题解析
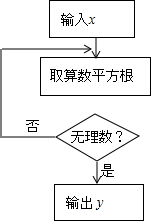16. 已知2a–1的平方根是± $\sqrt{17}$ ，3a+b–1的算术平方根是6，求a+4b的算术平方根.

查看试题解析
17. 一个正数b的两个平方根分别是 $2 a - 3$ 与 $5 - a$ ，

(1)、求 $a$ 和 $b$ 的值．

(2)、求 $5 a + b - 3$ 平方根．

查看试题解析

三、综合拓展

18. 如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示 $- \sqrt{2}$ ，设点B所表示的数为m．

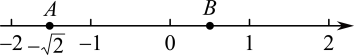(1)、求 $| m + 1 | + | m - 1 |$ 的值；

(2)、在数轴上还有C、D两点分别表示实数c和d，且有|2c＋6|与 $\sqrt{d - 4}$ 互为相反数，求2c+3d 的平方根．

查看试题解析
19. 阅读下列材料：如果一个数 $x$ 的 $n$ （ $n$ 是大于 $1$ 的整数）次方等于 $a$ ，这个数就 $x$ 叫做 $a$ 的 $n$ 次方根，即 $x^{n} = a$ ，则 $x$ 叫做 $a$ 的 $n$ 次方根．如： $2^{4} = 16$ ， ${(- 2)}^{4} = 16$ ，则 $2$ ， $- 2$ 是 $16$ 的 $4$ 次方根，或者说 $16$ 的 $4$ 次方根是 $2$ 和 $- 2$ ；再加 ${(- 2)}^{5} = - 32$ ，则 $- 2$ 叫做 $- 32$ 的 $5$ 次方根，或者说 $- 32$ 的 $5$ 次方根是 $- 2$ ．
回答问题：

(1)、 $64$ 的 $6$ 次方根是， $- 243$ 的 $5$ 次方根是， $0$ 的 $10$ 次方根是．

(2)、我们学习过一个数的平方根有以下的形质：一个正数的平方根有两个，它们互为相反数； $0$ 的平方根是 $0$ ；负数没有平方根．类比一个数的平方根的性质，归纳一个数的 $n$ （ $n$ 是大于 $1$ 的整数）次方根的性质．

查看试题解析