2.1《认识实数》（2）—北师大版数学八年级上册课堂分层训练

试卷更新日期：2025-08-13 类型：同步测试

进入出卷网下载

一、基础应用

1. 下列说法正确的是（）

A、无限小数都是无理数 B、无理数包括正无理数、0、负无理数 C、带根号的数都是无理数 D、实数与数轴上的点是一一对应的

查看试题解析
2. 实数a，b，c，d在数轴上对应点的位置如图所示，这四个实数中绝对值最小的是（）

A、a B、b C、c D、d

查看试题解析
3. $| - \frac{1}{2024} |$ 的相反数是( )

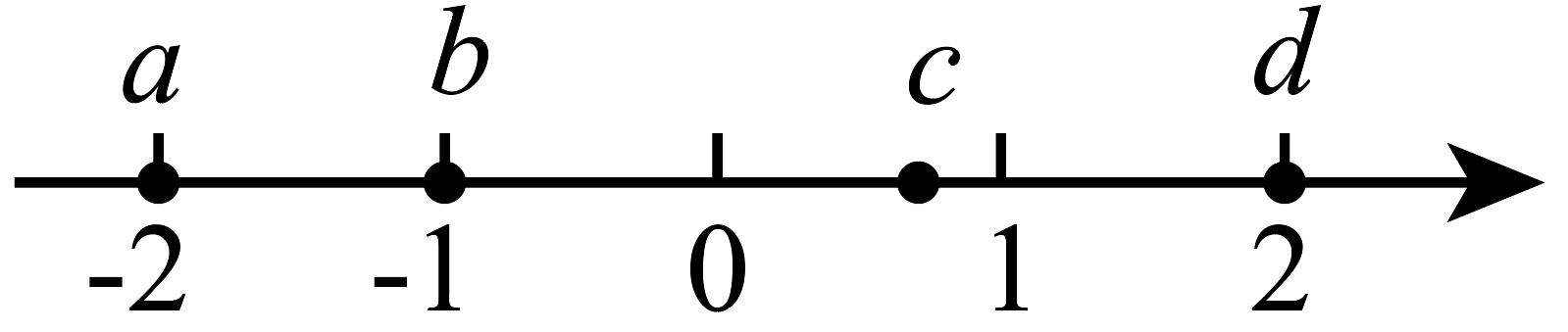A、 $- \frac{1}{2024}$ B、 $\frac{1}{2024}$ C、 $2024$ D、 $- 2024$

查看试题解析
4. 有-2，0， $π$ ， $\frac{1}{2}$ 四个数，其中最小的数是（）

A、-2 B、0 C、π D、 $\frac{1}{2}$

查看试题解析
5. 如图，圆的半径为1个单位长度，该圆上仅有点A与数轴上表示 $- 1$ 的点重合，将圆沿数轴负方向滚动一周，点A到达点 $A^{'}$ 的位置，则点 $A^{'}$ 表示的数是．

查看试题解析
6. 将下列各数填入相应的括号内：
$- 2.5$ ， $0$ ， $8$ ， $\frac{π}{2}$ ， $- 1.121121112 \dots$ ， $\frac{3}{4}$ ， $- 0.05$
正数集合：｛                                               …｝；
有理数集合：｛                                               …｝；
负数集合：｛                                               …｝；
无理数集合：｛                                               …｝．

查看试题解析
7. 把下列各数分别填入相应的大括号
$- 5$ ， 0， $| - 3.14 |$ ， $- \frac{22}{7}$ ， $0.1010010001 ⋯$ ， $+ 2.4$ ， $- 30 %$ ， $- (- 6)$ ， $- \frac{π}{3}$ ， $- | - 4 |$
正有理数集合：｛ …｝非正整数集合：｛ …｝
负分数集合：｛ …｝无理数集合：｛ …｝

查看试题解析
8. 把下列各数分别填入相应的集合里．
$| - 5.2 |$ ， 0， $\frac{π}{2}$ ， 227， $+ (- 4)$ ， $- 2 \frac{3}{4}$ ， $- 0.030030003 \dots$ ， $3.14$

(1)、正有理数集合：{                    …}；

(2)、无理数集合：{                       …}

(3)、非负整数集合：{                    …}；

(4)、分数集合：{                       …}

查看试题解析

二、能力提升

9. 如图，把直径为 1 个单位长度的圆从点 A 沿数轴向右滚动一周，圆上点A 到达点A'，点A'对应的数是2，则滚动前点A 对应的数是（）

A、2-2π B、π-2 C、5-2π D、2-π

查看试题解析
10. 设边长为a 的正方形的面积为2.下列有关于a的四种说法：①a是无理数；②a可以用数轴上的一个点来表示；③1＜a＜1.5 .其中，说法正确的有（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
11.

(1)、在- $\frac{1}{3} ， \frac{7}{4}$ ， 0，-1，0.4，π，2，-3，-6这些数中，有理数有m个，自然数有n个，分数有k个，则m-n-k的值为（）

A、1 B、2 C、3 D、4

(2)、下列说法中，正确的是（）

A、-a一定是负数 B、|a|一定是正数 C、|a|一定不是负数 D、-|a|一定是负数

查看试题解析
12. 下列说法中，正确的有( )
①实数不是有理数就是无理数；
②无限小数都是无理数；
③无理数都是无限小数；
④带根号的数都是无理数；
⑤两个无理数之和一定是无理数。

A、1个 B、2个 C、3个 D、4个

查看试题解析
13. 下列说法中，正确的有 ( )
①数轴上的点只能表示整数；
②数轴上的点所表示的数都是有理数；
③-a不一定是负数；
④符号相反的两个数互为相反数。

A、1个 B、2个 C、3个 D、4个

查看试题解析
14. 如图，若四个实数在数轴上的对应点分别为M，N，P，Q，则下列实数中，绝对值最大的是（）

A、点P表示的数 B、点Q表示的数 C、点M表示的数 D、点N表示的数

查看试题解析
15. 圆周率 $π$ 是一个无限不循环小数，中国古代数学家祖冲之算出 $π$ 的值在3.1415926至3.1415927之间，并找到了两个分数作为 $π$ 的近似值（约率 $\frac{22}{7}$ ，密率 $\frac{355}{113}$ ），这一成就曾经领先世界一千多年.则（）

A、 $π < \frac{22}{7}, π < \frac{355}{113}$ B、 $π > \frac{22}{7}, π < \frac{355}{113}$ C、 $π < \frac{22}{7}, π > \frac{355}{113}$ D、 $π > \frac{22}{7}, π > \frac{355}{113}$

查看试题解析
16. 把下列各数填在相应的大括号内：
$π ， - \frac{3}{4} ， - 12 ， 0 ， \frac{22}{7} ， 50 % ， - 3.14 ， 1.99 ， + 6 ， 0.101001000 . . .$ （每两个1之间依次多个0）：

(1)、正数集合： ${__________________________\dots}$ ；

(2)、无理数集合： ${__________________________\dots}$ ；

(3)、整数集合： ${__________________________\dots}$ ．

查看试题解析
17. 把下列各数填入表示它所在的数集的大括号：
$- 2.4$ ， 3， $- 2020$ ， $- \frac{10}{3}$ ， 0.1010010001…， $- 0 . \dot{1} \dot{5}$ ， 0， $- (- 30 %)$ ， $\frac{π}{3}$ ， $- | - 4 |$ .

(1)、正数集合：{…}；

(2)、无理数集合：{…}；

(3)、负分数集合：{…}；

(4)、非正整数集合：{…}.

查看试题解析

三、综合拓展

18. 我国著名数学家华罗庚曾说：“数缺形时少直观，形少数时难入微.”数形结合是解决数学问题的重要思想方法.数轴是数形结合的产物，用数轴上的点可以直观地表示实数，从而建立起“数”与“形”之间的联系.

(1)、如图1，点 $O$ 是原点，点 $A$ 对应的实数为 $- 2$ ，过点 $A$ 作 $A B$ 垂直于数轴，且 $A B = 1$ ，连接 $O B$ ，以 $O$ 为圆心， $O B$ 长为半径画弧，交数轴于点 $C$ ，那么点 $C$ 对应的实数为；

(2)、在（1）的条件下，若将线段 $O C$ 向右平移，使得点 $O$ 对应的实数为1，那么此时点 $C$ 对应的实数为；

(3)、如图2，点 $A$ 对应的实数是3，射线 $A B$ 垂直数轴于点 $A$ ，请在数轴上作出 $\sqrt{10} - 2$ 对应的点 $M$ .（要求：尺规作图并保留作图痕迹）

查看试题解析