浙教版（2024) 数学八年级上册1.1 认识三角形 同步分层练习

试卷更新日期：2025-08-12 类型：同步测试

进入 出卷网 下载

一、夯实基础：

  • 1. 以下列长度的线段为边，能够组成三角形的是（     ）
    A、3，6，9 B、3，5，9 C、2，6，4 D、4，6，9

    查看试题解析

  • 2. 若三角形的两边长分别为5，8，则第三条边的边长可能为（　　）
    A、2.5 B、3 C、7 D、13

    查看试题解析

  • 3. 如图，三角形有一部分被遮挡，我们可以判定此三角形的类型为（ ）

     

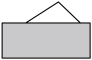    A、钝角三角形 B、直角三角形 C、锐角三角形 D、不能确定

    查看试题解析

  • 4. 已知△ABC中，∠A:∠B:∠C=1:2:3 ， 则△ABC是（     ）
    A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

    查看试题解析

  • 5. 用三根木棒首尾相接围成△ABC ， 若AC=5cm ， BC=8cm ， 设AB=xcm ， 则x的取值范围是（          ）
    A、x>3 B、x<13 C、3<x<13 D、3≤x≤13

    查看试题解析

  • 6. 已知三角形的三边均为正整数，其中两边为2，4，则第三边可以是 ． （请写出一个符合条件的值）

    查看试题解析

  • 7. 在△ABC中，∠A+∠B=90° ， 那么△ABC是（填“直角三角形”、“钝角三角形”或“锐角三角形”）

    查看试题解析

  • 8. 如图，已知AE为△ABC的中线，AB＝8cm ， AC＝6cm ， △ACE的周长为20cm ， 则△ABE的周长为 cm ．

    查看试题解析

二、能力提升：

  • 9. 如图，AD是△ABC的角平分线，AC∥DE，交AB于点E若∠BED=64°，则∠ADE的度数是（    ）

    A、23° B、26° C、32° D、37°

    查看试题解析

  • 10. 下列长度的三条线段，能首尾相接构成三角形的是（                ）
    A、1,2,3
     B、1,2,3
     C、2，2， 4
     D、2,3,6

    查看试题解析

  • 11. 下列各图中，正确画出AC边上的高的是（　　）
    A、    B、    C、    D、   

    查看试题解析

  • 12.  如图，CE是△ABC的外角∠ACF的平分线，且CE交BA的延长线于点E.若∠B=40°，∠E=30°则∠BAC的度数为.

    查看试题解析

三、拓展创新：

  • 13. 阅读与理解：

    三角形的中线的性质：三角形的中线等分三角形的面积，即如图1，AD是△ABC中BC边上的中线，则S△ABD=S△ACD=12S△ABC ．

    操作与探索：

    在图2至图4中，△ABC的面积为a．

    (1)、如图2，延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S1 ， 则S1= ． （用含a的代数式表示）．
    (2)、如图3，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S2 ， 则S2=（用含a的代数式表示）．
    (3)、在图3的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图4）．若图4中△DEF的面积为S3 ， 则S3=（用含a的代数式表示）．

    查看试题解析