浙教版数学九年级上册单元检测卷第1章 《二次函数》A卷
试卷更新日期:2025-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 在平面直角坐标系中,二次函数的图象与轴有两个交点,且这两个交点分别位于轴两侧,则下列关于该函数的结论正确的是( )A、图象的开口向下 B、当时,的值随值的增大而增大 C、函数的最小值小于 D、当时,2. 已知点 在抛物线 上,若 , 则下列判断正确的是( )A、 B、 C、 D、3. 已知抛物线的对称轴为直线 , 与轴的交点位于轴下方,且时, , 下列结论正确的是( )A、 B、 C、 D、4. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣4ac>0;③方程ax2+bx=0的两根为x1=﹣2,x2=0;④7a+c<0.其中正确的有( )
x
…
﹣3
﹣2
﹣1
1
2
…
y
…
1.875
3
m
1.875
0
…
A、①④ B、②③ C、③④ D、②④5. 已知二次函数(x是自变量)的图象经过第一、二、四象限,则实数a的取值范围为( )A、 B、 C、 D、6. 在同一平面直角坐标系中,函数y=ax﹣b(a≠0)和y(c≠0)的图象大致如图所示,则函数y=ax2+bx+c(a≠0)的图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 将抛物线y=x2+2x向下平移2个单位后,所得新抛物线的顶点式为( )A、y=(x+1)2﹣3 B、y=(x+1)2﹣2 C、y=(x﹣1)2﹣3 D、y=(x﹣1)2﹣28. 如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OM , 喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度与水平距离之间的关系式是 , 则水流喷出的最大高度是( )
7. 将抛物线y=x2+2x向下平移2个单位后,所得新抛物线的顶点式为( )A、y=(x+1)2﹣3 B、y=(x+1)2﹣2 C、y=(x﹣1)2﹣3 D、y=(x﹣1)2﹣28. 如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OM , 喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度与水平距离之间的关系式是 , 则水流喷出的最大高度是( ) A、3m B、2.75m C、2m D、1.75m9. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )
A、3m B、2.75m C、2m D、1.75m9. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )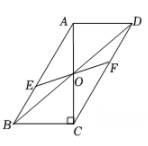 A、
A、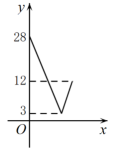 B、
B、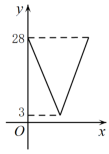 C、
C、 D、
D、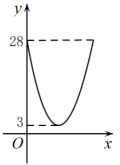 10. 如图,二次函数y=ax2+bx+c与x轴交于点A(3,0)、B(-1,0),与y轴交于点C(0,m),其中-4<-3.则下列结论:
10. 如图,二次函数y=ax2+bx+c与x轴交于点A(3,0)、B(-1,0),与y轴交于点C(0,m),其中-4<-3.则下列结论:①②方程没有实数根③④.
其中错误的个数有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
11. 已知二次函数 的图象经过点(c,0),但不经过原点,则该二次函数的表达式可以是.(写出一个即可)12. 如图,小亮同学掷铅球时,铅球沿抛物线y=a(×-3)2+2.5运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.若铅球抛出时离地面的高度OA为1.6m,则铅球掷出的水平距离OB为m.
 13. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴相交于点A , B , 点B的坐标为(3,0),若点C(2,3)在抛物线上,则AB的长为 .
13. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴相交于点A , B , 点B的坐标为(3,0),若点C(2,3)在抛物线上,则AB的长为 . 14. 如图, 壮壮同学投掷实心球, 出手 (点 处) 的高度 是 , 出手后实心球沿一段抛物线运行, 到达最高点时,水平距离是 , 高度是 . 若实心球落地点为 , 则OM=m。
14. 如图, 壮壮同学投掷实心球, 出手 (点 处) 的高度 是 , 出手后实心球沿一段抛物线运行, 到达最高点时,水平距离是 , 高度是 . 若实心球落地点为 , 则OM=m。 15. 如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系y=﹣0.02x2+0.3x+1.6的图象,点B(6,2.68)在图象上.若一辆箱式货车需在停车棚下避雨,货车截面看作长CD=4m , 高DE=1.8m的矩形,则可判定货车 完全停到车棚内(填“能”或“不能”).
15. 如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系y=﹣0.02x2+0.3x+1.6的图象,点B(6,2.68)在图象上.若一辆箱式货车需在停车棚下避雨,货车截面看作长CD=4m , 高DE=1.8m的矩形,则可判定货车 完全停到车棚内(填“能”或“不能”). 16. 抛物线(a , b , c是常数,)经过 , 两点,且 . 下列四个结论:
16. 抛物线(a , b , c是常数,)经过 , 两点,且 . 下列四个结论:①;
②若 , 则;
③若 , 则关于x的一元二次方程 无实数解;
④点 , 在抛物线上,若 , , 总有 , 则 .
其中正确的是(填写序号).
三、解答题(共8题,共72分)
-
17. 二次函数的图象经过点 , 且对称轴为直线 .(1)、求这个二次函数的解析式.(2)、若一个点的坐标满足 , 我们将这样的点定义为“倍值点”.
①求这个函数“倍值点”的坐标;
②若是该二次函数图象上“倍值点”之间的点(包括端点),求的最大值与最小值的差.
18. 用石块打水漂是一项有趣的活动.抛掷后的石块与平静的水面接触.石块会在空中近似的形成一组抛物线的运动路径.如图①,小星站在河边的安全位置用一个石块打水漂,石块在空中飞行的高度y与水平距离之间的关系如图②所示.石块第一次与水面接触于点 , 运动路径近似为抛物线 , 且 , 石块在水面上弹起后第二次与水面接触于点 , 运动路径近似为抛物线 , 且 . (小星所在地面、水面在同一平面内,且石块形状大小、空气阻力等因素忽略不计)
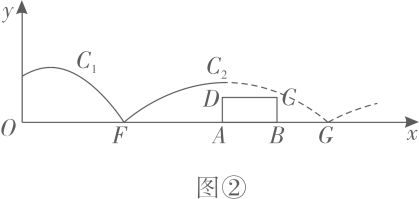 (1)、如图②,当时,若点坐标为 , 求抛物线的表达式;(2)、在(1)的条件下,若 , 在水面上有一个截面宽 , 高的矩形的障碍物,点的坐标为 , 判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;(3)、小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中 , 求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)19. 已知二次函数y=x2+2(a+1)x+3a2-2a+3,a为常数.(1)、若该二次函数的图象与直线y=2a2有两个交点,求a的取值范围;(2)、若该二次函数的图象与x轴有交点,求a的值;(3)、求证:该二次函数的图象不经过原点.20. 2025年春节期间,我国国产动画电影《哪吒之魔童闹海》刷新了中国电影票房的新纪录,商家推出A、B两款“哪吒”文旅纪念品.已知购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元.(1)、求A、B两款“哪吒”纪念品每个进价分别的多少元?(2)、根据网上预约的情况,如果该商家计划用不超过12000元的资金购进A、B两款“哪吒”纪念品共400个,那么至少需要购进B款纪念品多少个?(3)、在销售中,该商家发现每个A款纪念品售价60元时,可售出200个,售价每增加1元,销售量将减少5个.设每个A款纪念品售价元,W表示该商家销售A款纪念品的利润(单位:元),求W关于a的函数表达式,并求出W的最大值.21. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .
(1)、如图②,当时,若点坐标为 , 求抛物线的表达式;(2)、在(1)的条件下,若 , 在水面上有一个截面宽 , 高的矩形的障碍物,点的坐标为 , 判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;(3)、小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中 , 求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)19. 已知二次函数y=x2+2(a+1)x+3a2-2a+3,a为常数.(1)、若该二次函数的图象与直线y=2a2有两个交点,求a的取值范围;(2)、若该二次函数的图象与x轴有交点,求a的值;(3)、求证:该二次函数的图象不经过原点.20. 2025年春节期间,我国国产动画电影《哪吒之魔童闹海》刷新了中国电影票房的新纪录,商家推出A、B两款“哪吒”文旅纪念品.已知购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元.(1)、求A、B两款“哪吒”纪念品每个进价分别的多少元?(2)、根据网上预约的情况,如果该商家计划用不超过12000元的资金购进A、B两款“哪吒”纪念品共400个,那么至少需要购进B款纪念品多少个?(3)、在销售中,该商家发现每个A款纪念品售价60元时,可售出200个,售价每增加1元,销售量将减少5个.设每个A款纪念品售价元,W表示该商家销售A款纪念品的利润(单位:元),求W关于a的函数表达式,并求出W的最大值.21. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .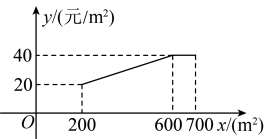 (1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?22. 已知抛物线为常数, .
(1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?22. 已知抛物线为常数, .(I)当时,求该抛物线顶点的坐标;
(II)点和点为抛物线与轴的两个交点,点为抛物线与轴的交点.
①当时,若点在抛物线上, , 求点的坐标;
②若点 , 以AC为边的的顶点在抛物线的对称轴上,当取得最小值为时,求顶点的坐标.
23. 如图1,抛物线()与轴交于 , 两点,与轴交于点 . (1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.24. 如图,直线交轴于点 , 交轴于点 , 对称轴为的抛物线经过两点,交轴负半轴于点 . 为抛物线上一动点,点的横坐标为 , 过点作轴的平行线交抛物线于另一点 , 作轴的垂线 , 垂足为 , 直线交轴于点 .
(1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.24. 如图,直线交轴于点 , 交轴于点 , 对称轴为的抛物线经过两点,交轴负半轴于点 . 为抛物线上一动点,点的横坐标为 , 过点作轴的平行线交抛物线于另一点 , 作轴的垂线 , 垂足为 , 直线交轴于点 .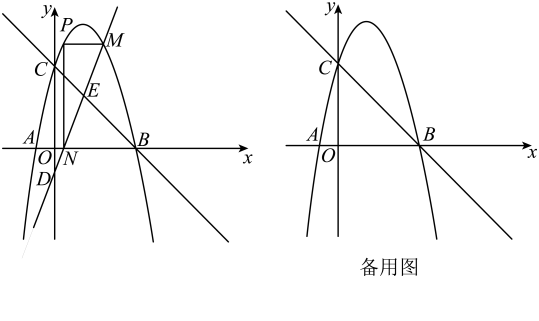 (1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.