浙教版数学九年级上册单元检测卷第1章《二次函数》B卷

试卷更新日期：2025-08-11 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，一个圆形喷水池的中央竖直安装了一个柱形喷水装置OM，喷头M向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，按如图所示的直角坐标系，水流喷出的高度y（m）与水平距离x（m）之间的关系式是 $y = - x^{2} + 2 x + \frac{7}{4} (x > 0)$ ，则水流喷出的最大高度是（）

A、3m B、2.75m C、2m D、1.75m

查看试题解析
2. 已知点（﹣2，y₁），（3，y₂），（7，y₃）都在二次函数y＝﹣（x﹣2）²+c的图象上，则y₁ ， y₂ ， y₃的大小关系是（　　）

A、y₁＞y₂＞y₃ B、y₁＞y₃＞y₂ C、y₂＞y₁＞y₃ D、y₃＞y₂＞y₁

查看试题解析
3. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则（）

A、 $a b c < 0$ B、 $2 a + b < 0$ C、 $2 b - c < 0$ D、 $a - b + c < 0$

查看试题解析
4. 已知抛物线 $y = (x - 2)^{2} + 1$ ，下列结论错误的是（）

A、抛物线开口向上 B、抛物线的对称轴为直线 $x = 2$ C、抛物线的顶点坐标为 $(2 ， 1)$ D、当 $x < 2$ 时，y随x的增大而增大

查看试题解析
5. 已知二次函数 $y = x^{2} - 2 a x + a (a \neq 0)$ 的图象经过 $A (\frac{a}{2}, y_{1}), B (3 a, y_{2})$ 两点，则下列判断正确的是（）

A、可以找到一个实数 $a$ ，使得 $y_{1} > a$ B、无论实数 $a$ 取什么值，都有 $y_{1} > a$ C、可以找到一个实数 $a$ ，使得 $y_{2} < 0$ D、无论实数 $a$ 取什么值，都有 $y_{2} < 0$

查看试题解析
6. 点A (m-1，y₁)，B(m，y₂)都在二次函数y=(x-1)²+n的图象上。若y₁<y₂ ，则m的取值范围为（）

A、m>2 B、m> $\frac{3}{2}$ C、m<1 D、 $\frac{3}{2}$ <m<2

查看试题解析
7. 在平面直角坐标系中，二次函数 $y = a x^{2} - 2 a x + a - 3 (a \neq 0)$ 的图象与 $x$ 轴有两个交点，且这两个交点分别位于 $y$ 轴两侧，则下列关于该函数的结论正确的是（）

A、图象的开口向下 B、当 $x > 0$ 时， $y$ 的值随 $x$ 值的增大而增大 C、函数的最小值小于 $- 3$ D、当 $x = 2$ 时， $y < 0$

查看试题解析
8. 在水分、养料等条件一定的情况下，某植物的生长速度 $y ($ 厘米 $/$ 天 $)$ 和光照强度 $x ($ 勒克斯 $)$ 之间存在一定关系．在低光照强度范围 $(200 \leq x < 1000)$ 内， $y$ 与 $x$ 近似成一次函数关系；在中高光照强度范围 $(x \geq 1000)$ 内， $y$ 与 $x$ 近似成二次函数关系．其部分图象如图所示．根据图象，下列结论正确的是（）

A、当 $x \geq 1000$ 时， $y$ 随 $x$ 的增大而减小 B、当 $x = 2000$ 时， $y$ 有最大值 C、当 $y \geq 0.6$ 时， $x \geq 1000$ D、当 $y = 0.4$ 时， $x = 600$

查看试题解析
9. 如图，已知抛物线 $y = a x^{2} + b x + c$ （ $a 、 b 、 c$ 为常数，且 $a \neq 0$ ）的对称轴是直线 $x = 1$ ，且抛物线与 $x$ 轴的一个交点坐标是 $(4, 0)$ ，与 $y$ 轴交点坐标是 $(0, m)$ 且 $2 < m < 3$ ．有下列结论：① $a b c < 0$ ；② $9 a - 3 b + c > 0$ ；③ $\frac{9}{4} < y_{最大值} < \frac{27}{8}$ ；④关于 $x$ 的一元二次方程 $a x^{2} + (b - 1) x + c - 2 = 0$ 必有两个不相等实根；⑤若点 $A (x_{1}, y_{1}), B (x_{2}, y_{2}), C (x_{3}, y_{3})$ 在抛物线 $y = a x^{2} + b x + c$ 上，
且 $n < x_{1} < n + 1 < x_{2} < n + 2 < x_{3} < n + 3$ ，当 $y_{1} < y_{3} < y_{2}$ 时，则 $n$ 的取值范围为 $- \frac{3}{2} < n < 0$ ．
其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的一部分与x轴的一个交点坐标为 $(1 ， 0)$ ，对称轴为 $x = - 1$ ，结合图象给出下列结论：

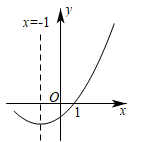
① $a + b + c = 0$ ；

② $a - 2 b + c < 0$ ；

③关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两根分别为-3和1；

④若点 $(- 4 ， y_{1})$ ， $(- 2 ， y_{2})$ ， $(3 ， y_{3})$ 均在二次函数图象上，则 $y_{1} < y_{2} < y_{3}$ ；

⑤ $a - b < m (a m + b)$ （m为任意实数）．

其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共18分）

11. 抛物线 $y = 3 x^{2}$ 向下平移两个单位所得的抛物线解析式为.

查看试题解析
12. 将二次函数y=2x²﹣1的图象沿y轴向上平移2个单位，所得图象对应的函数表达式为．

查看试题解析
13. 抛物线 $y = x^{2} - 6 x + c$ 与 $x$ 轴只有一个交点，则 $c =$ ．

查看试题解析
14. 在平面直角坐标系中，将抛物线 $y = x^{2} + 2 x - 1$ 先绕原点旋转180°，再向下平移5个单位，所得到的抛物线的顶点坐标是.

查看试题解析
15. 抛物线 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 是常数， $c < 0$ ）经过 $(1 ， 1) ， (m ， 0) ， (n ， 0)$ 三点，且 $n \geq 3$ ．下列四个结论：
① $b < 0$ ；

② $4 a c - b^{2} < 4 a$ ；

③当 $n = 3$ 时，若点 $(2 ， t)$ 在该抛物线上，则 $t > 1$ ；

④若关于 $x$ 的一元二次方程 $a x^{2} + b x + c = x$ 有两个相等的实数根，则 $0 < m \leq \frac{1}{3}$ ．

其中正确的是（填写序号）．

查看试题解析
16. 对于一个二次函数 $y = a (x - m)^{2} + k$ （ $a \neq 0$ ）中存在一点 $P (x^{'}, y^{'})$ ，使得 $x^{'} - m = y^{'} - k \neq 0$ ，则称 $2 | x^{'} - m |$ 为该抛物线的“开口大小”，那么抛物线 $y = - \frac{1}{2} x^{2} + \frac{1}{3} x + 3$ “开口大小”为．

查看试题解析

三、解答题（共8题，共72分）

17. 如图，抛物线 $y = x^{2} + b x + c$ 交x轴于点A、点B ，交y轴于点C ，且点A在点B的左侧，顶点坐标为 $(3, - 4)$ ．

(1)、求b与c的值。

(2)、在x轴上方的抛物线上是否存在点P ，使 $△ P B C$ 的面积与 $△ A B C$ 的面积相等．若存在，请直接写出点P的横坐标；若不存在，请说明理由。

查看试题解析
18. 已知抛物线 $y = a x^{2} + b x + c$ 与x轴只有一个公共点.

(1)、若抛物线过点 P(0，1)，求a+b的最小值.

(2)、已知点 P₁(-2，1)，P₂(2，-1)，P₃(2，1)中恰有两点在抛物线上.
①求抛物线的解析式.
②设直线l：y= kx+1与抛物线交于M，N两点，点A 在直线y=--1上，且∠MAN=90°，过点 A 且与x 轴垂直的直线分别交抛物线和l 于点 B，C.求证：△MAB 与△MBC 的面积相等.

查看试题解析
19. 小星路过某广场时看到一处喷泉景观，喷出的水柱呈抛物线形状（如图1）．如图2是他对此展开研究的示意图，喷出的水柱是抛物线 $y = - \frac{1}{5} x^{2} + \frac{4}{5} x + c$ 的一部分，测得喷头 $A$ 距离地面的高度 $O A = 1$ 米．

(1)、求该抛物线的表达式．

(2)、若小星身高1.6米，他站在水柱下方而没有被淋湿，设小星与喷头 $A$ 的水平距离为 $a$ 米，求 $a$ 的取值范围．

(3)、为了让喷泉景观更加壮观，需要让喷泉水柱的落地点 $B$ 与喷头 $A$ 的水平距离OB不小于6米，但不能超过8米．若仅改变喷头 $A$ 的高度，设喷头 $A$ 的高度为 $h$ ，试确定 $h$ 的取值范围．

查看试题解析
20. 在平面直角坐标系xOy中，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 经过点 O和点A(3，3a).

(1)、求c的值，并用含a的式子表示b；

(2)、过点 P(t，0)作x轴的垂线，交抛物线于点 M，交直线y= ax于点N.
①若a=1，t =4，求MN的长；
②已知在点P从点O运动到点B(2a，0)的过程中，MN的长随OP的长的增大而增大，求a的取值范围.

查看试题解析
21. 如图，抛物线 $L : y = \frac{1}{4} x^{2} + b x - 3$ （b为常数）．

(1)、求证：抛物线L一定与x轴有两个交点，并且这两个交点分居在原点的两侧；

(2)、当抛物线L经过点 $M (- 4, m) ， N (6, m)$ 时，
①求抛物线L的顶点坐标，并直接写出抛物线L与x轴在原点右侧的交点坐标；
②若 $0 \leq x \leq n$ 时，函数 $y = \frac{1}{4} x^{2} + b x - 3$ 的最大值与最小值的差总为 $\frac{1}{4}$ ，求n的取值范围．

查看试题解析
22. 数学兴趣小组在学习二次函数后，发现二次函数中字母系数与其图象有直接联系，他们借助学习函数的经验，对二次函数 $y = x^{2} - 2 m x + m (m$ 为常数）进行研究．
【特例分析】
（1）数学兴趣小组分别取 $m = 1, 2, 3$ 三个特殊值进行特例研究．
①确定表达式：
当 $m = 1$ 时， $y_{1} = x^{2} - 2 x + 1$ ，当 $m = 2$ 时， $y_{2} = x^{2} - 4 x + 2$ ，当 $m = 3$ 时， $y_{3} =$ ____________；
②画函数图象：
平面直角坐标系中已画出 $y_{1}$ 和 $y_{2}$ 的图象，请你在同一坐标系中画出 $y_{3}$ 的图象；
【性质探究】
（2）数学兴趣小组通过观察图象得到猜想：不论 $m$ 为何值，二次函数 $y = x^{2} - 2 m x + m$ 图象经过点 $(\frac{1}{2}, \frac{1}{4})$ ．请问这个猜想是否正确？请说明理由．
【性质应用】
（3）已知点 $A (- 2, - 5), B (2, - 1)$ ，若二次函数 $y = x^{2} - 2 m x + m$ 图象与线段 $A B$ 有且只有一个交点，求 $m$ 的取值范围．

查看试题解析
23. 如图所示，已知二次函数 $y = a x^{2} - \frac{5}{3} x$ 图象与直线 $y = - x + m$ 相交于点 $A (5, 0)$ ，直线交 $y$ 轴于 $B$ ，点 $P$ 为抛物线上一点，将点 $P$ 绕着原点 $O$ 逆时针旋转 $90 °$ 得到对应点 $Q$ ，连接 $P Q$ ．

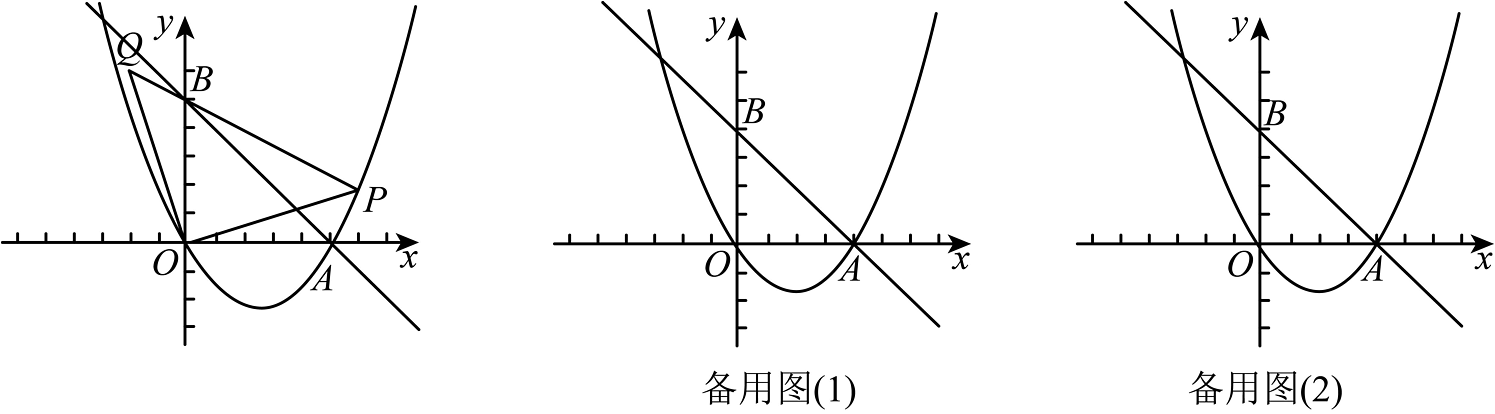(1)、求抛物线和直线 $A B$ 的函数解析式．

(2)、当点 $P$ 坐标为 $(6, 2)$ 时，求证：点 $P$ ， $Q$ ， $B$ 三点在同一直线上．

(3)、当 $△ O P Q$ 有一顶点在直线 $A B$ 上时，
①求 $P Q$ 长；
②在①的条件下，当点 $P$ 在第四象限时，在 $P Q$ 上取点 $C$ ，在 $O P$ 上取点 $D$ ，使 $Q C = P D$ ，连接 $O C$ ， $D Q$ ，求 $O C + D Q$ 的最小值．

查看试题解析
24. 如图，在平面直角坐标系中，O为坐标原点，抛物线y＝x²+bx﹣1经过点（2，﹣1）．点P在此抛物线上．其横坐标为m；连接PO并延长至点Q ，使OQ＝2PO ．当点P不在坐标轴上时，过点P作x轴的垂线，过点Q作y轴的垂线，这两条垂线交于点M ．

(1)、求此抛物线对应的函数解析式．

(2)、△PQM被y轴分成的两部分图形的面积比是否保持不变，如果不变，直接写出这个面积比；如果变化，说明理由．

(3)、当△PQM的边MQ经过此抛物线的最低点时，求点Q的坐标．

(4)、当此抛物线在△PQM内部的点的纵坐标y随x的增大而减小时，直接写出m的取值范围．

查看试题解析

浙教版数学九年级上册单元检测卷第1章 《二次函数》B卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

浙教版数学九年级上册单元检测卷第1章《二次函数》B卷