浙教版数学九年级上册单元检测卷第3章 《圆的基本性质》A卷
试卷更新日期:2025-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,均为的半径,连接 , 若 , , 则的度数为( )
 A、 B、 C、 D、2. 如图,是的弦,半径于点 . 若 . 则的长是( )
A、 B、 C、 D、2. 如图,是的弦,半径于点 . 若 . 则的长是( ) A、3 B、2 C、6 D、3. 如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°,则∠A=( )
A、3 B、2 C、6 D、3. 如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°,则∠A=( ) A、66° B、33° C、24° D、30°4. 在锐角三角形ABC中,AB=AC,BC=8,它的外接圆O的半径长为5,若点D是边AC的中点,以点D为圆心的圆和⊙O相交,那么⊙D的半径长可以是( )A、2 B、5 C、8 D、105. 如图,四边形ABCD内接于⊙O, , 连接BD,若∠ABC=70°,则∠BDC的度数为( )
A、66° B、33° C、24° D、30°4. 在锐角三角形ABC中,AB=AC,BC=8,它的外接圆O的半径长为5,若点D是边AC的中点,以点D为圆心的圆和⊙O相交,那么⊙D的半径长可以是( )A、2 B、5 C、8 D、105. 如图,四边形ABCD内接于⊙O, , 连接BD,若∠ABC=70°,则∠BDC的度数为( ) A、20° B、35° C、55° D、70°6. 如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
A、20° B、35° C、55° D、70°6. 如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( ) A、1 B、 C、2 D、27. 如图, AB是⊙O的直径, ∠CAB=40°, 则∠ADC的度数是( )
A、1 B、 C、2 D、27. 如图, AB是⊙O的直径, ∠CAB=40°, 则∠ADC的度数是( ) A、80° B、50° C、40° D、25°8. 如图,在矩形ABCD中,分别以点A,C为圆心,AD 长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A、80° B、50° C、40° D、25°8. 如图,在矩形ABCD中,分别以点A,C为圆心,AD 长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( ) A、32-8π B、 C、32-4π D、9. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
A、32-8π B、 C、32-4π D、9. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ). A、1.0厘米/分 B、0.8厘米/分 C、1.2厘米/分 D、1.4厘米/分10. 如图,半径为 5 的 扇 形 AOB 中,∠AOB=90°,C 是 上一点,CD⊥OA,CE⊥OB,垂足分别为 D,E.若CD=CE,则图中阴影部分的面积为( )
A、1.0厘米/分 B、0.8厘米/分 C、1.2厘米/分 D、1.4厘米/分10. 如图,半径为 5 的 扇 形 AOB 中,∠AOB=90°,C 是 上一点,CD⊥OA,CE⊥OB,垂足分别为 D,E.若CD=CE,则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 已知⊙O的半径为5cm.若点P在⊙O上,则点P到圆心O的距离为cm.12. 如图,是的弦.半径于点D,且 . 则的长是 .
 13. 如图,△ABC内接于⊙O , AD是直径,若∠B=25°,则∠CAD=°.
13. 如图,△ABC内接于⊙O , AD是直径,若∠B=25°,则∠CAD=°. 14. 如图,点A , B , C在⊙O上,∠BAC=50°,则∠OBC= °.
14. 如图,点A , B , C在⊙O上,∠BAC=50°,则∠OBC= °. 15. 如图,△ABC是⊙O的内接三角形,∠BAC=45°.若⊙O的半径为2,则劣弧的长为.
15. 如图,△ABC是⊙O的内接三角形,∠BAC=45°.若⊙O的半径为2,则劣弧的长为. 16. 如图,的半径为1,A , B , C是上的三个点.若四边形为平行四边形,连接AC , 则图中阴影部分的面积为 .
16. 如图,的半径为1,A , B , C是上的三个点.若四边形为平行四边形,连接AC , 则图中阴影部分的面积为 .
三、解答题(共8题,共72分)
-
17. 如图,已知是的直径,点在上, .
 (1)、求证:;(2)、求的度数.18. 如图,四边形ABCD的顶点都在半圆O上,AB是半圆O的直径,连接OC,.
(1)、求证:;(2)、求的度数.18. 如图,四边形ABCD的顶点都在半圆O上,AB是半圆O的直径,连接OC,. (1)、 求证:;(2)、 若 , , 求AB的长.19. 如图,等腰三角形的顶角 , 和底边相切于点 , 并与两腰 , 分别相交于 , 两点,连接 , .
(1)、 求证:;(2)、 若 , , 求AB的长.19. 如图,等腰三角形的顶角 , 和底边相切于点 , 并与两腰 , 分别相交于 , 两点,连接 , . (1)、求证:四边形是菱形;(2)、若的半径为2,求图中阴影部分的面积.20. 如图,在中, , 以为直径作 , 与相交于点 . 连接 , 与相交于点 .
(1)、求证:四边形是菱形;(2)、若的半径为2,求图中阴影部分的面积.20. 如图,在中, , 以为直径作 , 与相交于点 . 连接 , 与相交于点 . (1)、如图1,连接 , 求的度数;(2)、如图2,若点为的中点,且 , 求的长.21. 如图,是的外接圆,D是直径AB上一点,的平分线交AB于点E , 交于另一点F , .
(1)、如图1,连接 , 求的度数;(2)、如图2,若点为的中点,且 , 求的长.21. 如图,是的外接圆,D是直径AB上一点,的平分线交AB于点E , 交于另一点F , . (1)、求证:;(2)、设 , 垂足为M , 若 , 求AC的长.22. 如图,已知是等边三角形的外接圆,连接并延长交于点 , 交于点 , 连接 , .
(1)、求证:;(2)、设 , 垂足为M , 若 , 求AC的长.22. 如图,已知是等边三角形的外接圆,连接并延长交于点 , 交于点 , 连接 , . (1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.23. 如图所示,四边形是半径为R的的内接四边形,是的直径, , 直线l与三条线段、、的延长线分别交于点E、F、G.且满足 .
(1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.23. 如图所示,四边形是半径为R的的内接四边形,是的直径, , 直线l与三条线段、、的延长线分别交于点E、F、G.且满足 .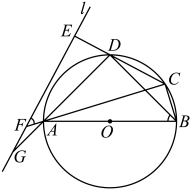 (1)、求证:直线直线;(2)、若;
(1)、求证:直线直线;(2)、若;①求证:;
②若 , 求四边形的周长.
24. 【实际情境】手工课堂上,老师给每个制作小组发放一把花折伞和制作花折伞的材料及工具.同学们认真观察后,组装了花折伞的骨架,粘贴了彩色伞面,制作出精美的花折伞.

 (1)、【模型建立】
(1)、【模型建立】如图1,从花折伞中抽象出“伞形图”. , .求证:.
(2)、【模型应用】如图2,中,的平分线交于点D.请你从以下两个条件:
①;②中选择一个作为已知条件,另一个作为结论,并写出结论成立的证明过程.(注:只需选择一种情况作答)
(3)、【拓展提升】如图3,为的直径, , 的平分线交于点E , 交于点D , 连接.求证:.