浙教版数学九年级上册单元检测卷第4章 《相似三角形》A卷
试卷更新日期:2025-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列各组中的四条线段成比例的是( )A、a=2,b=3,c=4,d=1 B、a=2, b= , c= , d= C、a=4,b=6,c=5,d=10 D、a= , b=3,c=2,d=2. 如图,在中, , , , , 则的长为( )
 A、2 B、4 C、6 D、83. 如图,直线 , 直线AC分别交于点;直线DF分别交于点 . 若 , 则EF的长为( )
A、2 B、4 C、6 D、83. 如图,直线 , 直线AC分别交于点;直线DF分别交于点 . 若 , 则EF的长为( ) A、6 B、5 C、4 D、34. 小李在做“小孔成像”实验时,蜡烛到挡板的距离与挡板到屏幕的距离之比是 . 若烛焰的高是 , 则实像的商是( )
A、6 B、5 C、4 D、34. 小李在做“小孔成像”实验时,蜡烛到挡板的距离与挡板到屏幕的距离之比是 . 若烛焰的高是 , 则实像的商是( ) A、 B、 C、 D、5. 如图,在平面直角坐标系中,的顶点坐标分别是 , , , 以原点为位似中心,在第三象限画与位似,若与的相似比为 , 则点的对应点的坐标为( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,的顶点坐标分别是 , , , 以原点为位似中心,在第三象限画与位似,若与的相似比为 , 则点的对应点的坐标为( ) A、 B、 C、 D、6. 已知 , 则下列式子不成立的是( )A、 B、 C、 D、7. 如图,在四边形中, , 点E在上,交于点F , 若 , , 则的长为( )
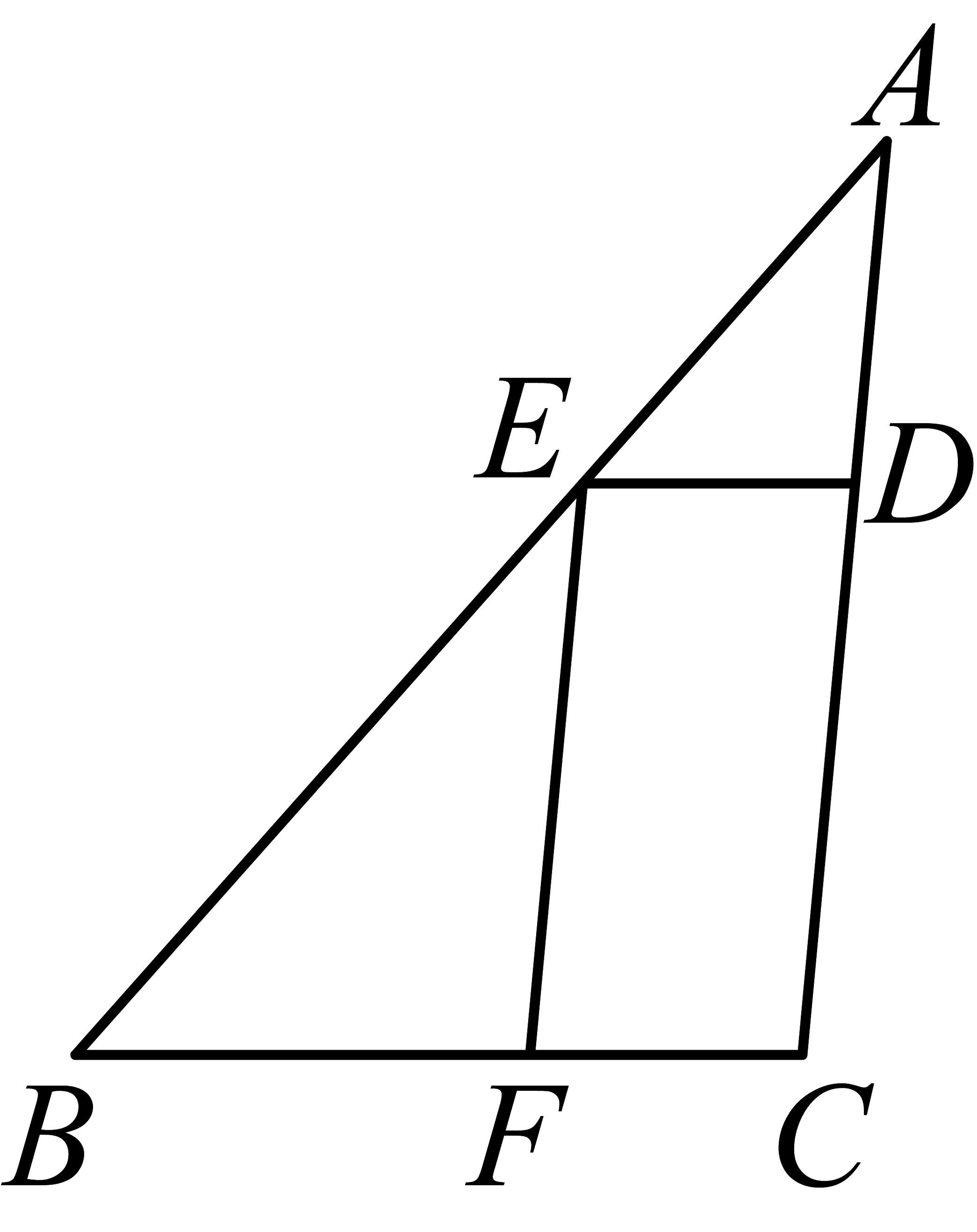
A、 B、 C、 D、6. 已知 , 则下列式子不成立的是( )A、 B、 C、 D、7. 如图,在四边形中, , 点E在上,交于点F , 若 , , 则的长为( ) A、6 B、4 C、5 D、4.58. 如图,正方形的边长是6,E在对角线上,且 , 过作于 , 连接并延长交于 , 交的延长线于 . 则( )
A、6 B、4 C、5 D、4.58. 如图,正方形的边长是6,E在对角线上,且 , 过作于 , 连接并延长交于 , 交的延长线于 . 则( )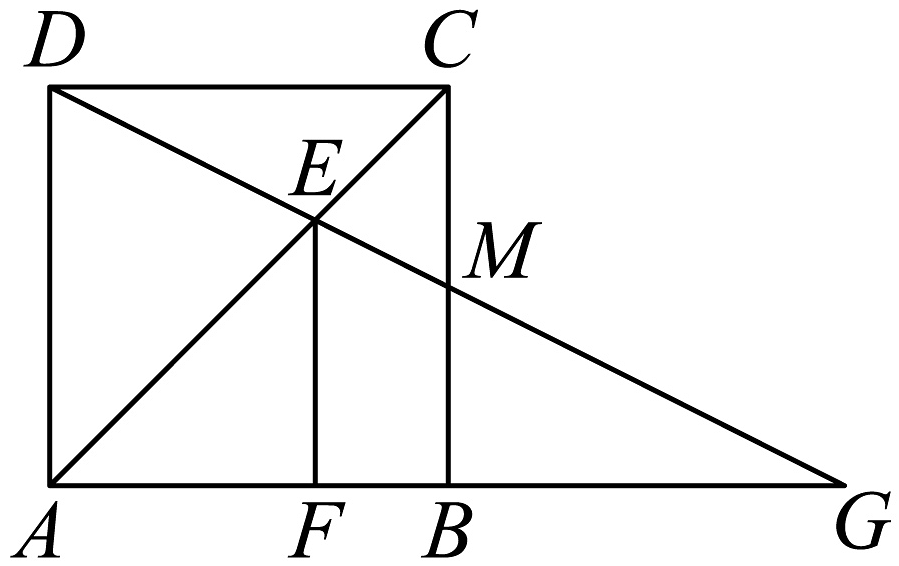 A、 B、 C、 D、9. 如图,在△ABC中,D,E分别为边AB,AC的中点.下列结论中,错误的是( )
A、 B、 C、 D、9. 如图,在△ABC中,D,E分别为边AB,AC的中点.下列结论中,错误的是( ) A、DE∥BC B、△ADE∽△ABC C、BC=2DE D、10. 如图,点A为反比例函数图象上的一点,连接 , 过点O作的垂线与反比例的图象交于点B,则的值为( )
A、DE∥BC B、△ADE∽△ABC C、BC=2DE D、10. 如图,点A为反比例函数图象上的一点,连接 , 过点O作的垂线与反比例的图象交于点B,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 在平面直角坐标系中,把△ABC以原点O为位似中心放大,得到△A'B'C'.若点A和它的对应点A'的坐标分别为(3,7),(-9,-21),则△ABC与△A'B'C'的相似比为.12. 如图,四边形 ABCD是菱形,对角线. 于点E,交 AC于点 F,则 .
 13. 如图,△ABC与△A´B´C´位似,点 O为位似中心,若AA´=3OA´,B´C´=5,则 BC的长为.
13. 如图,△ABC与△A´B´C´位似,点 O为位似中心,若AA´=3OA´,B´C´=5,则 BC的长为. 14. 如图,D 是等边△ABC 的边AB 上的一点,且 现将△ABC 折叠,使点 C 与点 D 重合,折痕为EF,点 E,F 分别在AC 和BC上,则 。
14. 如图,D 是等边△ABC 的边AB 上的一点,且 现将△ABC 折叠,使点 C 与点 D 重合,折痕为EF,点 E,F 分别在AC 和BC上,则 。 15. 如图,在中, , 分别是边 , 上的中线,与相交于点 , 点 , 分别在上,四边形是平行四边形.若 , 则的长度为 .
15. 如图,在中, , 分别是边 , 上的中线,与相交于点 , 点 , 分别在上,四边形是平行四边形.若 , 则的长度为 .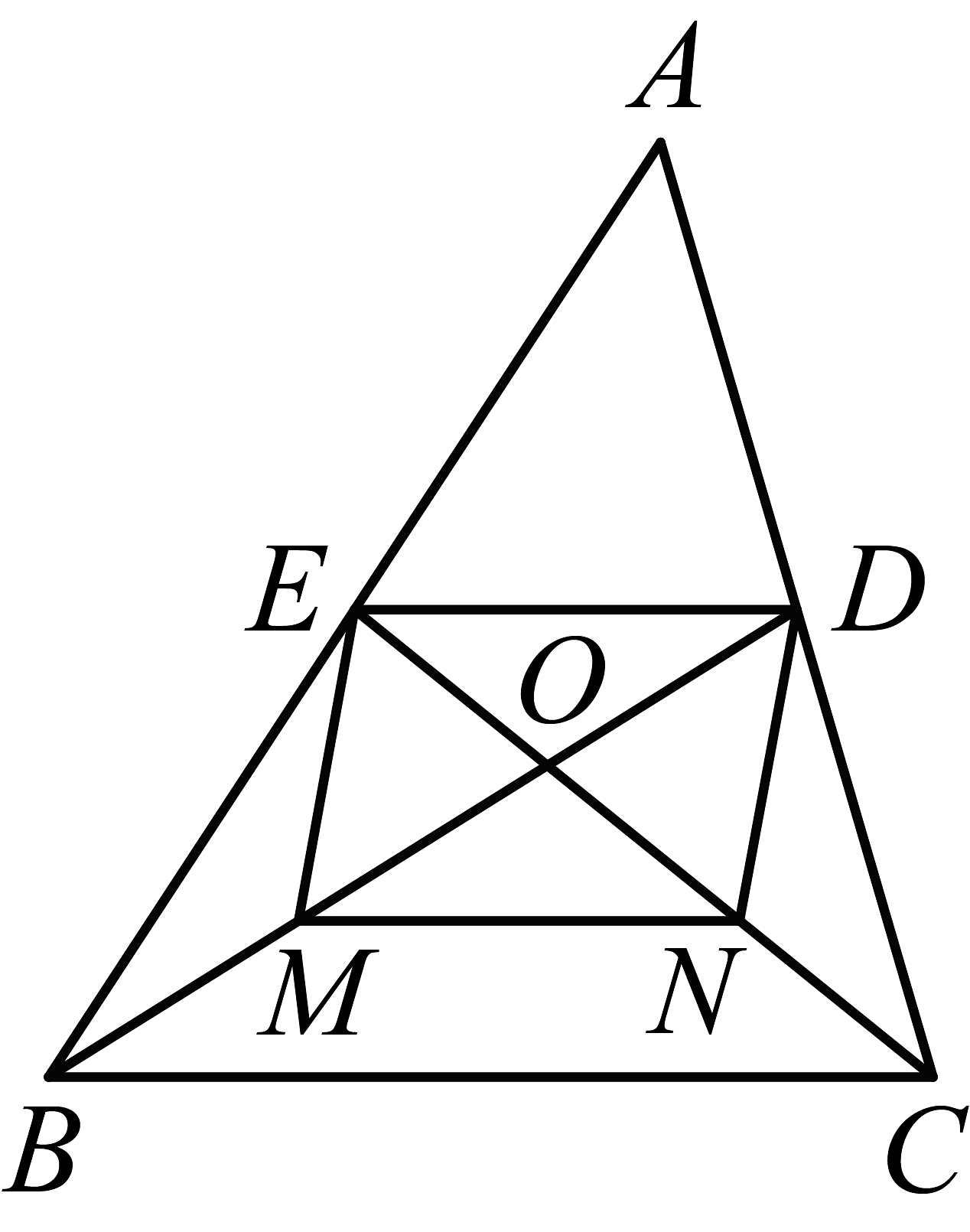 16. 如图,在中,点D,E分别在AB,BC边上, , 且 , 则的值为.
16. 如图,在中,点D,E分别在AB,BC边上, , 且 , 则的值为.
三、解答题(共8题,共72分)
-
17. 如图,在锐角三角形中, . 以点为圆心,长为半径画弧,交边于点 , 连结 , 点是延长线上的一点,连结 , 若平分 .
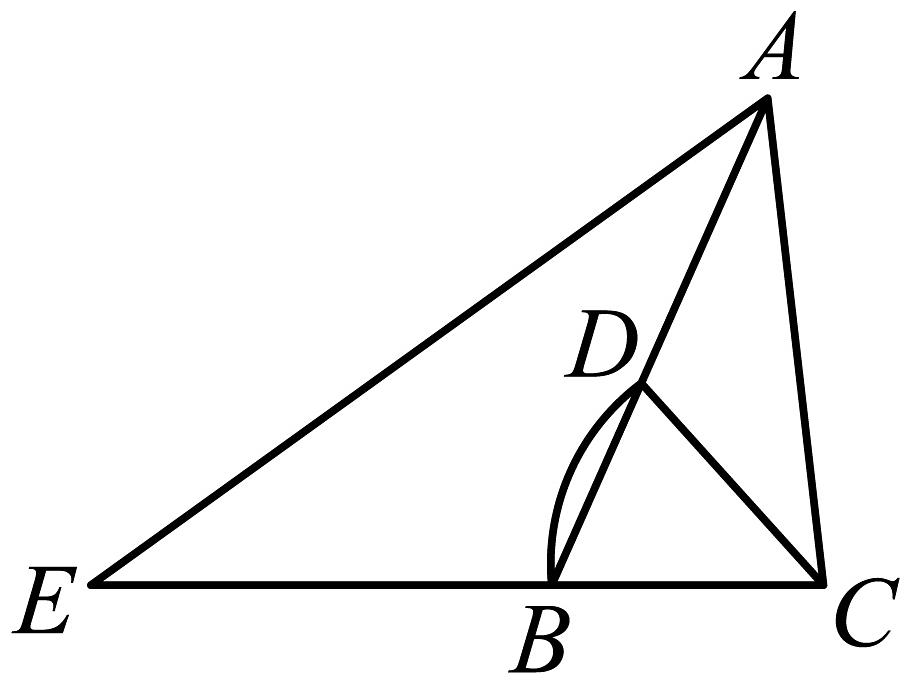 (1)、求证:;(2)、当 , 求的值.18. 如图,在△ABC中,点 D,E,F分别在边 AB,AC,BC 上,连 结 DE,EF. 已 知 四 边 形BFED是平行四边形,
(1)、求证:;(2)、当 , 求的值.18. 如图,在△ABC中,点 D,E,F分别在边 AB,AC,BC 上,连 结 DE,EF. 已 知 四 边 形BFED是平行四边形, (1)、若AB=15,求线段BD的长;(2)、若△ADE 的面积为 3,求▱BFED 的面积.19. 如图甲所示,在平行四边形 ABCD 中,E 是AB 中点,连结DE 并延长,交CB 的延长线于点F.
(1)、若AB=15,求线段BD的长;(2)、若△ADE 的面积为 3,求▱BFED 的面积.19. 如图甲所示,在平行四边形 ABCD 中,E 是AB 中点,连结DE 并延长,交CB 的延长线于点F. (1)、求证:(2)、如图乙所示,连结CE,过点 A 作. 交DE 于点G.求证:EC20. 如图所示,已知矩形ABCD,点E 在CB 延长线上,点 F 在BC 延长线上,过点F 作FH⊥EF 交ED 的延长线于点 H,连结 AF 交EH 于点G,GE=GH.
(1)、求证:(2)、如图乙所示,连结CE,过点 A 作. 交DE 于点G.求证:EC20. 如图所示,已知矩形ABCD,点E 在CB 延长线上,点 F 在BC 延长线上,过点F 作FH⊥EF 交ED 的延长线于点 H,连结 AF 交EH 于点G,GE=GH. (1)、求证:BE=CF;(2)、当 时,求 EF 的长.21. 如图,在边长为2的正方形ABCD中,E是边AD上一点,以BE为直角边向外作等腰直角三角形BEF , 且∠BEF=90°,BF和EF分别交CD于点M , N . 解答下列问题:
(1)、求证:BE=CF;(2)、当 时,求 EF 的长.21. 如图,在边长为2的正方形ABCD中,E是边AD上一点,以BE为直角边向外作等腰直角三角形BEF , 且∠BEF=90°,BF和EF分别交CD于点M , N . 解答下列问题: (1)、当E为AD中点时,求DN , CM的长;(2)、当CM=DN时,求AE的长.22. 如图,△ABC中,BC=12,S△ABC=36,点D是边AB上一点,过点D作DE//BC交AC于点E,以DE 为边作矩形 DEFG,其中点F、G落在边BC上.
(1)、当E为AD中点时,求DN , CM的长;(2)、当CM=DN时,求AE的长.22. 如图,△ABC中,BC=12,S△ABC=36,点D是边AB上一点,过点D作DE//BC交AC于点E,以DE 为边作矩形 DEFG,其中点F、G落在边BC上. (1)、当AD=BD 时,求矩形 DEFG 的面积;(2)、当DE 经过△ABC 的重心时,求矩形 DEFG的面积.
(1)、当AD=BD 时,求矩形 DEFG 的面积;(2)、当DE 经过△ABC 的重心时,求矩形 DEFG的面积.

