浙教版数学九年级上册单元检测卷第3章 《圆的基本性质》B卷
试卷更新日期:2025-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 图1是通过平面图形的镶嵌所呈现的图案,图2是其局部放大示意图,由正六边形、正方形和正三角形构成,它的轮廓为正十二边形,则图2中∠ABC的大小是( )
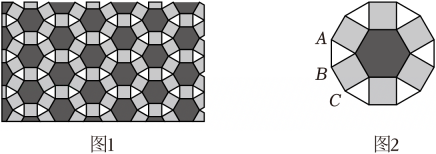 A、90° B、120° C、135° D、150°2. 如图,AB为⊙O的直径,点C,D是⊙O上位于AB异侧的两点,连接AD,CD.若 , 则∠D的度数为( )
A、90° B、120° C、135° D、150°2. 如图,AB为⊙O的直径,点C,D是⊙O上位于AB异侧的两点,连接AD,CD.若 , 则∠D的度数为( ) A、30° B、45° C、60° D、75°3. 点A,B,C在⊙O上的位置如图所示,∠A=70°,⊙O的半径为3,则的长是( )
A、30° B、45° C、60° D、75°3. 点A,B,C在⊙O上的位置如图所示,∠A=70°,⊙O的半径为3,则的长是( ) A、 B、 C、 D、7π4. 如图,AB 是⊙O 的直径,弦CD 与AB垂直,垂足为E,连结CO并延长,交⊙O于点F,∠CDB=30°,CD=2 则图中阴影部分的面积为( )
A、 B、 C、 D、7π4. 如图,AB 是⊙O 的直径,弦CD 与AB垂直,垂足为E,连结CO并延长,交⊙O于点F,∠CDB=30°,CD=2 则图中阴影部分的面积为( ) A、 B、 C、 D、5. 如图, AC, BC为⊙O的弦, 连接OA, OB, OC.若∠AOB=40°, ∠OCA=30°,则∠BCO的度数为( )
A、 B、 C、 D、5. 如图, AC, BC为⊙O的弦, 连接OA, OB, OC.若∠AOB=40°, ∠OCA=30°,则∠BCO的度数为( ) A、40° B、45° C、50° D、55°6. 如图,CD是⊙O的直径,AB是弦,AB⊥CD , ∠ADC=30°,则∠BOC=( )
A、40° B、45° C、50° D、55°6. 如图,CD是⊙O的直径,AB是弦,AB⊥CD , ∠ADC=30°,则∠BOC=( ) A、30° B、45° C、60° D、75°7. 如图,在△ABC中,∠BAC=90°,AB=AC,分别以点B,C为圆心、BC的长为半径画弧,与BA,CA的延长线分别交于点D,E.若BC=4,则图中阴影部分的面积为( )
A、30° B、45° C、60° D、75°7. 如图,在△ABC中,∠BAC=90°,AB=AC,分别以点B,C为圆心、BC的长为半径画弧,与BA,CA的延长线分别交于点D,E.若BC=4,则图中阴影部分的面积为( ) A、2π-4 B、4π-4 C、8π-8 D、4π-88. 如图,在 Rt中,是边上的中线,其中 , 以为圆心,为半径画弧交于点 , 则的长为( )
A、2π-4 B、4π-4 C、8π-8 D、4π-88. 如图,在 Rt中,是边上的中线,其中 , 以为圆心,为半径画弧交于点 , 则的长为( ) A、 B、 C、 D、9. 如图,四边形ABCD内接于⊙O , , 连接BD , 若 , 则的度数为( )
A、 B、 C、 D、9. 如图,四边形ABCD内接于⊙O , , 连接BD , 若 , 则的度数为( ) A、20° B、35° C、55° D、70°10. 如图,扇形OAB 中,∠AOB=100°,OA=12,C是OB 的中点,CD⊥OB 交 于点D,以OC 为半径的CE交OA 于点E,则图中阴影部分的面积是( ).
A、20° B、35° C、55° D、70°10. 如图,扇形OAB 中,∠AOB=100°,OA=12,C是OB 的中点,CD⊥OB 交 于点D,以OC 为半径的CE交OA 于点E,则图中阴影部分的面积是( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图, AB为⊙O的弦, OC⊥AB于点C, 连接OA, OB,若AB=OA, AC=3, 则OA的长为.
 12. 如图,六边形 ABCDEF是⊙O的内接正六边形,设正六边形ABC-DEF的面积为S1 , △ACE 的面积为 S2 , 则 .
12. 如图,六边形 ABCDEF是⊙O的内接正六边形,设正六边形ABC-DEF的面积为S1 , △ACE 的面积为 S2 , 则 . 13. 如图,为的直径, , , 则的度数为 .
13. 如图,为的直径, , , 则的度数为 . 14. 我国魏晋时期数学家刘徽在为《九章算术》作注时,创立了“割圆术”.如图是研究“割圆术”时的一个图形,所在圆的圆心为点O , 四边形ABCD为矩形,边CD与相切于点 , 连接 , 连接OE交AB于点 . 若 , 则图中阴影部分的面积为 .
14. 我国魏晋时期数学家刘徽在为《九章算术》作注时,创立了“割圆术”.如图是研究“割圆术”时的一个图形,所在圆的圆心为点O , 四边形ABCD为矩形,边CD与相切于点 , 连接 , 连接OE交AB于点 . 若 , 则图中阴影部分的面积为 . 15. 如图,已知是的圆周角, , 则°
15. 如图,已知是的圆周角, , 则° 16. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为.
16. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为.
三、解答题(共8题,共72分)
-
17. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点 M 在⊙O 上,MD恰好经过圆心O,连结MB.
 (1)、若CD=8,BE=2,求⊙O的半径;(2)、若AB=10,∠M=∠D,求的长.18. 如图,都是的半径, .
(1)、若CD=8,BE=2,求⊙O的半径;(2)、若AB=10,∠M=∠D,求的长.18. 如图,都是的半径, . (1)、求证:;(2)、若 , 求的半径.19. 如图,已知⊙O的半径为 四边形 ABCD 内接于⊙O,连结 AC,BD,DB=DC,∠BDC=45°
(1)、求证:;(2)、若 , 求的半径.19. 如图,已知⊙O的半径为 四边形 ABCD 内接于⊙O,连结 AC,BD,DB=DC,∠BDC=45° (1)、求的长;(2)、求证:AD 平分△ABC的外角∠EAC.20. 如图,内接于 , 是的直径,与交于点E , 于点F , 且平分 .
(1)、求的长;(2)、求证:AD 平分△ABC的外角∠EAC.20. 如图,内接于 , 是的直径,与交于点E , 于点F , 且平分 . (1)、求证:;(2)、若 , 垂足为G , 且 , 请补全图形,并求出的长.21. 如图,点 , , 在上,于点 , 交于点 , 连接 , 于点 , 与相文于点 .
(1)、求证:;(2)、若 , 垂足为G , 且 , 请补全图形,并求出的长.21. 如图,点 , , 在上,于点 , 交于点 , 连接 , 于点 , 与相文于点 . (1)、求证:;(2)、若 , , 求的半径.22. 如图,点 C 为△ABD 外接圆上的一动点(点 C 不在 上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)、求证:;(2)、若 , , 求的半径.22. 如图,点 C 为△ABD 外接圆上的一动点(点 C 不在 上,且不与点B,D重合),∠ACB=∠ABD=45°. (1)、求证:BD 是该外接圆的直径.(2)、连接CD,求证:(3)、若△ABC 关于直线AB 的对称图形为△ABM,连接DM,试探究DM2 , AM2 , BM2三者之间满足的数量关系,并证明你的结论.23. 如图1所示,等边三角形内接于圆 , 点是劣弧上任意一点(不与重合),连接、、 .
(1)、求证:BD 是该外接圆的直径.(2)、连接CD,求证:(3)、若△ABC 关于直线AB 的对称图形为△ABM,连接DM,试探究DM2 , AM2 , BM2三者之间满足的数量关系,并证明你的结论.23. 如图1所示,等边三角形内接于圆 , 点是劣弧上任意一点(不与重合),连接、、 .
【初步探索】
(1)将绕点顺时针旋转到 , 使点与点重合,可得、、三点在同一直线上,则线段、、存在的数量关系是:________________.
【知识迁移】
(2)如图1所示,若圆的半径为8,问的最大值是多少?
【拓展延伸】
(3)如图2所示,等腰内接于圆 , , 点是弧上任一点(不与重合),连接、、 , 若圆的半径为8,试求周长的最大值.
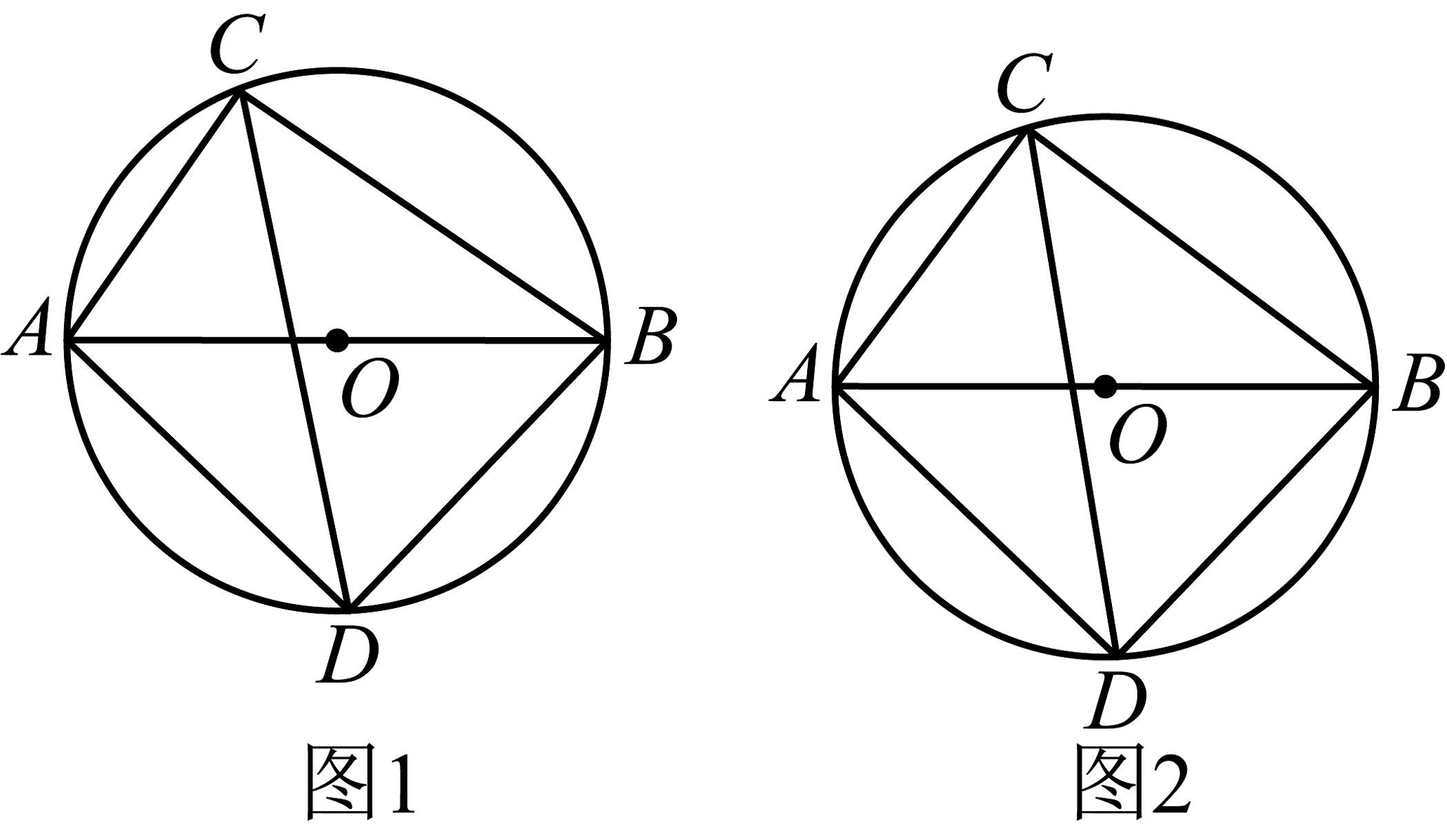
24. 回归课本(1)如图1.的直径为 , 弦为 , 的平分线交于点 , 则______________________ .
深挖问题
(2)在(1)的条件下,求的长.
探究发现
(3)如图2.为的直径,为上的一点(不与点重合),的平分线交于点 , 记 , 请直接写出和之间的数量关系.