浙教版数学九年级上册单元检测卷第4章 《相似三角形》B卷
试卷更新日期:2025-08-11 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 用放大镜将一个△ABC的面积放大为原来的 4 倍,则放大后的( )A、∠A,∠B、∠C是原来的4倍 B、周长是原来的2倍 C、对应边长是原来的4倍 D、对应中线长是原来的4倍2. 如图,以点O为位似中心的△ABC与△DEF的周长比为2:3,则OA:AD的值是( )
 A、4:9 B、3:1 C、2:1 D、2:33. 如图, , 若 , , 则与的相似比是( )
A、4:9 B、3:1 C、2:1 D、2:33. 如图, , 若 , , 则与的相似比是( ) A、 B、 C、 D、4. 图①是伸缩折叠不锈钢晾衣架图,图②是它的侧面示意图,AD 与CB 相交于点O,AB∥CD,根据图②中的数据可得x 的值为( )
A、 B、 C、 D、4. 图①是伸缩折叠不锈钢晾衣架图,图②是它的侧面示意图,AD 与CB 相交于点O,AB∥CD,根据图②中的数据可得x 的值为( ) A、0.8 B、0.96 C、1 D、1.085. 如图,在矩形ABCD中,AB=8,BC=4,点E 在AB 上,点 F 在CD上,点G,H 在对角线AC.上,若四边形 EGFH 是菱形,则AE 的长是( ).
A、0.8 B、0.96 C、1 D、1.085. 如图,在矩形ABCD中,AB=8,BC=4,点E 在AB 上,点 F 在CD上,点G,H 在对角线AC.上,若四边形 EGFH 是菱形,则AE 的长是( ). A、2 B、3 C、5 D、66. 如图,在平面直角坐标系中,的顶点为 , , . 以点为位似中心,在第三象限内作与的位似比为的位似图形 , 则点的坐标为( )
A、2 B、3 C、5 D、66. 如图,在平面直角坐标系中,的顶点为 , , . 以点为位似中心,在第三象限内作与的位似比为的位似图形 , 则点的坐标为( ) A、 B、 C、 D、7. 如图,在四边形ABCD中,对角线AC与BD相交于点O,则下列说法正确的是( )
A、 B、 C、 D、7. 如图,在四边形ABCD中,对角线AC与BD相交于点O,则下列说法正确的是( ) A、若OA·OC=OB·OD,则BC//AD B、若OA·BD=OB·AC,则BC//AD C、若OA·OB=OC·OD,则BC//AD D、若OA·OD=OB·OC,则BC//AD8. 如图,线段AD,BC交于点 , 连接AB,CD。若 , , 则CE的长为( )
A、若OA·OC=OB·OD,则BC//AD B、若OA·BD=OB·AC,则BC//AD C、若OA·OB=OC·OD,则BC//AD D、若OA·OD=OB·OC,则BC//AD8. 如图,线段AD,BC交于点 , 连接AB,CD。若 , , 则CE的长为( ) A、 B、 C、 D、9. 如图,在中, , , .点E是AC的中点,连接DE,且 , , 则( )
A、 B、 C、 D、9. 如图,在中, , , .点E是AC的中点,连接DE,且 , , 则( ) A、4 B、 C、 D、10. 在正方形中, , 点是边的中点,连接 , 延长至点 , 使得 , 过点作 , 分别交、于两点,连接 , , , 下列结论:①;②;③;④ . 正确的是( )
A、4 B、 C、 D、10. 在正方形中, , 点是边的中点,连接 , 延长至点 , 使得 , 过点作 , 分别交、于两点,连接 , , , 下列结论:①;②;③;④ . 正确的是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题(每题3分,共18分)
-
11. 唢呐是山西八大套的乐器之一,如图,一个大唢呐AB的长约为56cm,若在唢呐上喇叭端的一个黄金分割点P处进行装饰,且 , 则该装饰与吹口的距离AP为cm(结果保留根号).
 12. 当时,则 .13. 如图,在正方形中,是边上靠近的三等分点,是的中点,是对角线上的动点,当取得最小值时,的值是 .
12. 当时,则 .13. 如图,在正方形中,是边上靠近的三等分点,是的中点,是对角线上的动点,当取得最小值时,的值是 . 14. 如图,在中, , 且 , 若的面积为 , 则四边形的面积为 .
14. 如图,在中, , 且 , 若的面积为 , 则四边形的面积为 . 15. 如图,的顶点在反比例函数的图象上,点在轴上,点 , 在轴上,与轴交于点 , 连接 , 若 , , 则的值为 .
15. 如图,的顶点在反比例函数的图象上,点在轴上,点 , 在轴上,与轴交于点 , 连接 , 若 , , 则的值为 .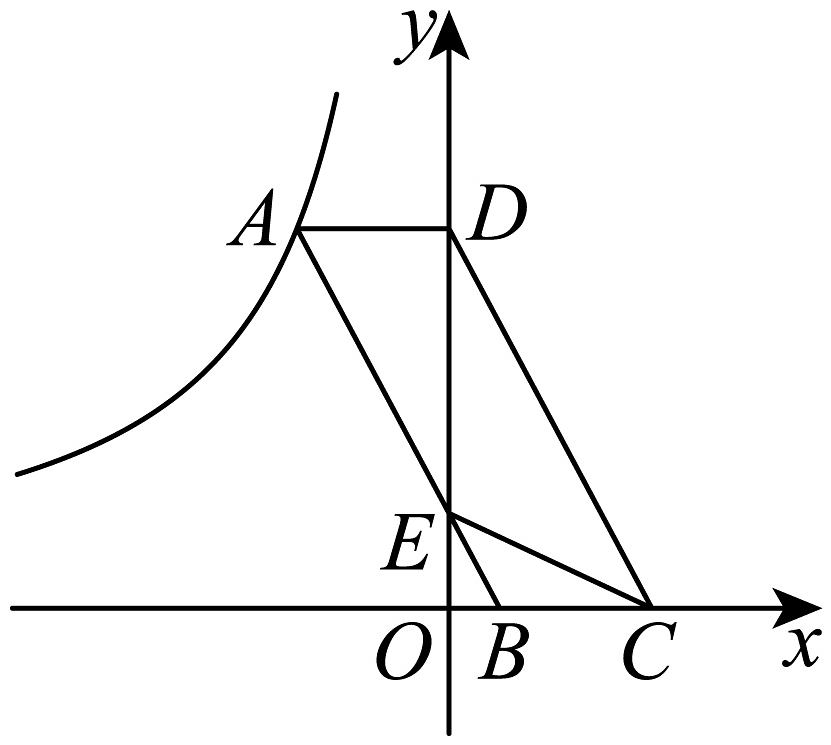 16. 在矩形 中, , 点 在直线 上, 且 , 则点 到矩形对角线所在直线的距离是.
16. 在矩形 中, , 点 在直线 上, 且 , 则点 到矩形对角线所在直线的距离是.三、解答题(共8题,共72分)
-
17. 如图所示,BC,AD 相交于点C,△ABC∽△DEC,AC=4.8,CD=1.6,BC=9.3.
 (1)、求CE 的长.(2)、求证:BC⊥AD.18. 如图,在Rt中,已知 , 点在AC上.连结BD,过点作交BD于点 , 交BC于点.
(1)、求CE 的长.(2)、求证:BC⊥AD.18. 如图,在Rt中,已知 , 点在AC上.连结BD,过点作交BD于点 , 交BC于点. (1)、求证:.(2)、过点作交AC于点 , 若 , 求AG的长.19. 如图,在矩形中, ,点 分别在边 上,满足 .
(1)、求证:.(2)、过点作交AC于点 , 若 , 求AG的长.19. 如图,在矩形中, ,点 分别在边 上,满足 . (1)、求证∶ .(2)、若 ,求的长.20. 如图,在四边形中,平分 .
(1)、求证∶ .(2)、若 ,求的长.20. 如图,在四边形中,平分 . (1)、证明:;(2)、已知 , 求的长.21. 如图,在⊙O中,AB和CD是弦,半径OA、OB分别交CD于点E、F,且CE=DF.
(1)、证明:;(2)、已知 , 求的长.21. 如图,在⊙O中,AB和CD是弦,半径OA、OB分别交CD于点E、F,且CE=DF. (1)、求证:AB//CD;(2)、若AB=BD,求证:AB2=BF·OB.22. 问题:如图1,点P为正方形ABCD内一个动点,过点P作EF∥AD , GH∥AB , 矩形PHCF的面积是矩形PGAE面积的2倍,探索∠FAH的度数随点P运动的变化情况.
(1)、求证:AB//CD;(2)、若AB=BD,求证:AB2=BF·OB.22. 问题:如图1,点P为正方形ABCD内一个动点,过点P作EF∥AD , GH∥AB , 矩形PHCF的面积是矩形PGAE面积的2倍,探索∠FAH的度数随点P运动的变化情况.
【从特例开始】
(1)、小玲利用正方形网格画出了一个符合条件的特殊图形(如图2),请你仅用无刻度的直尺连接一条线段,由此可得此图形中∠FAH= °.(2)、小亮也画出了一个符合条件的特殊图形(如图3),其中PE=PF=6,PG=4,PH=8,求此图形中∠FAH的度数;(3)、【一般化探索】利用图1,探索上述问题中∠FAH的度数随点P运动的变化情况,并说明理由.
23. 在等腰中, , 点是BC边上一点(不与点B,~C重合),连结AD. (1)、如图1,若 , 点关于直线AB的对称点为点 , 连结AE,DE,则(2)、若 , 将线段AD绕点顺时针旋转得到线段AE,连结BE.
(1)、如图1,若 , 点关于直线AB的对称点为点 , 连结AE,DE,则(2)、若 , 将线段AD绕点顺时针旋转得到线段AE,连结BE.①在图2中补全图形;
②探究CD与BE的数量关系,并证明;
(3)、如图3,若 , 且 . 试探究BE、BD、AC之间满足的数量关系,并证明.24. 如图,在菱形中, , 点为线段上一动点,点为射线上的一点(点与点不重合).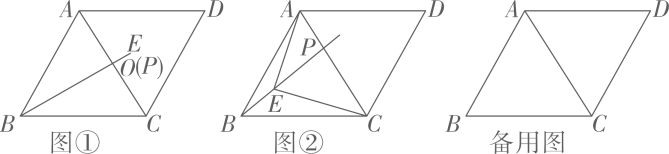 (1)、【问题解决】
(1)、【问题解决】如图①,若点与线段的中点重合,则度,线段与线段的位置关系是;
(2)、【问题探究】如图②,在点运动过程中,点在线段上,且 , 探究线段与线段的数量关系,并说明理由;
(3)、【拓展延伸】在点运动过程中,将线段绕点逆时针旋转得到 , 射线交射线于点 , 若 , 求的长.