1.3 《勾股定理的应用》（2）—北师大版数学八年级上册课堂分层训练

试卷更新日期：2025-08-11 类型：同步测试

进入出卷网下载

一、基础应用

1. 如图所示，将一根 $24cm$ 的筷子，置于底面直径为 $15cm$ ，高 $8cm$ 的圆柱形水杯中，设筷子露在杯子外面的长度 $h$ $cm$ ，则h的取值范围是（）

A、 $h \leq 17 cm$ B、 $h \geq 8 cm$ C、 $15 cm < h \leq 16 cm$ D、 $7 cm \leq h \leq 16 cm$

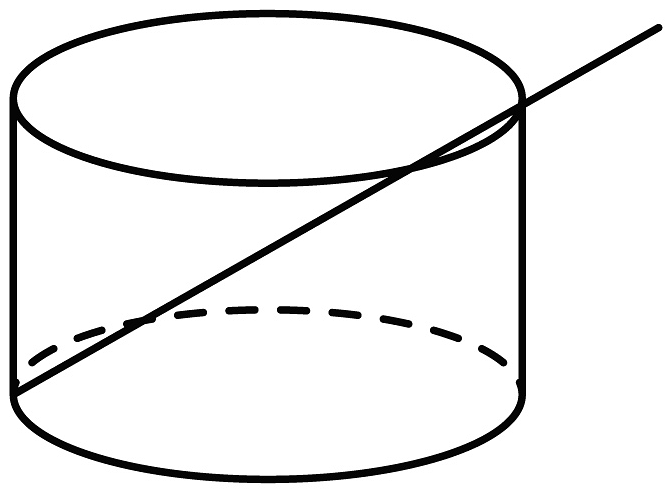查看试题解析
2. 临汾是帝尧之都，有着尧都之称．尧都华表柱身祥云腾龙，顶蹲冲天吼，底座浮雕长城和黄河壶口瀑布，是中华民族历史悠久、文化灿烂的标志．如图，在底面周长约为6米且带有层层回环不断的云朵石柱上，有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方（从点A到点C，B为 $A C$ 的中点），每根华表刻有雕龙的部分的柱身高约16米，则雕刻在石柱上的巨龙至少为（）

A、20米 B、25米 C、30米 D、15米

查看试题解析
3. 如图，湖的两岸有A，C两点，在与AC成直角的BC方向上的点C处测得AB＝15米，BC＝12米，则A，C两点间的距离为（）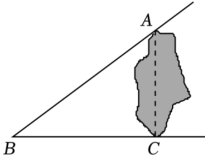

A、3米 B、6米 C、9米 D、10米

查看试题解析
4. 如图，一根长为 $5 m$ 的竹竿 $A B$ 斜靠在竖直的墙壁上，竹竿底端B离墙壁距离 $3 m$ ，则该竹竿的顶端A离地竖直高度为（）

A、 $2 m$ B、 $3 m$ C、 $4 m$ D、 $\sqrt{3} m$

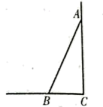查看试题解析
5. 长方体的长宽高分别是3、4、2，一只蚂蚁沿着长方体的外表面从 $A$ 点爬到 $B$ 点，最短路径长为．

查看试题解析
6. 如图所示：分别以直角三角形 $A B C$ 三边为边向外作三个正方形，其面积分别用 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 表示，若 $S_{1} = 25$ ， $S_{3} = 9$ ，则 $B C$ 的长为．

查看试题解析
7. 如图，一只蚂蚁要从A处沿圆柱体的侧面爬到B处，已知圆柱体的高是12，底面圆周长是10，则蚂蚁爬行的最短路径为．

查看试题解析
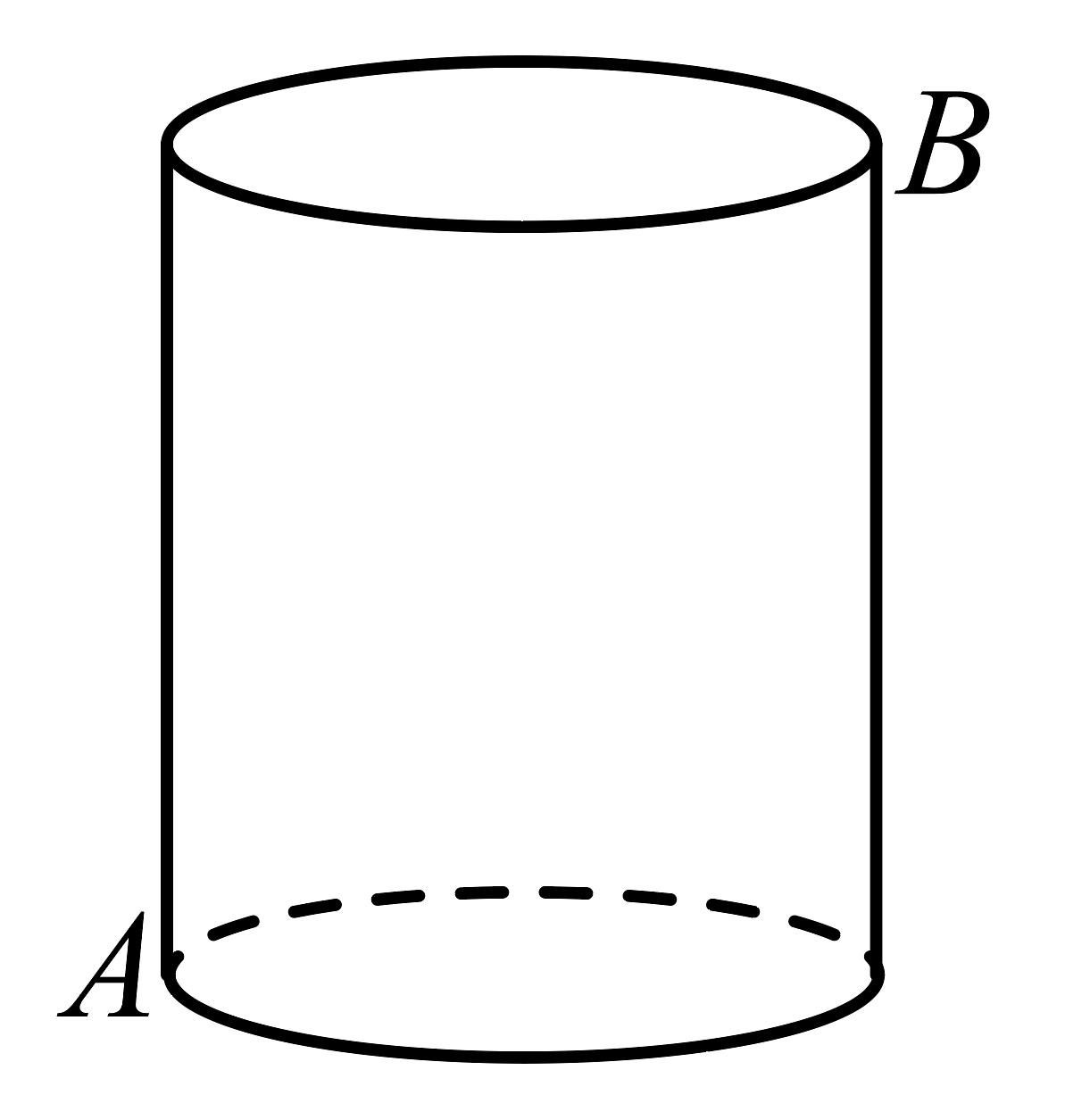8. 请解决我国古代数学著作《九章算术》中的一个问题：一根竹子原来高9尺，从 $A$ 处折断，折断后竹子顶端 $B$ 点落在离竹子底端 $O$ 点3尺处，求折断处离地面（即 $A O$ ）的高度是多少尺？

查看试题解析

二、能力提升

9. 解决下列几个问题，并说明它们与本节课问题的区别与联系.

(1)、如图，圆柱的高为13cm，底面周长为10cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到离上底面1cm的点B处的食物，那么它沿圆柱侧面爬行的最短路程是多少?

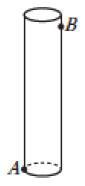(2)、如图，一个长方体形盒子的长、宽、高分别为8cm， 8cm，12cm，一只蚂蚁想从盒底的点 A 处沿盒的外表面爬到盒顶的点 B处，你能帮蚂蚁设计一条最短的路线吗?蚂蚁爬行的最短路程是多少?

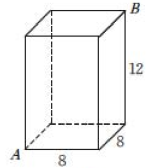(3)、为了营造节日气氛，学校准备在大厅圆柱上缠绕彩带.已知大厅圆柱的高为6m，底面周长为2m.如果希望彩带从圆柱底端绕圆柱4圈后正好到达顶端，那么至少需要彩带多少米?

查看试题解析
10. 如图，教室墙面 $A D E F$ 与地面 $A B C D$ 垂直，点 $P$ 在墙面上，若 $P A = \sqrt{13}$ 米， $A B = 2$ 米，点 $P$ 到 $A F$ 的距离是3米，一只蚂蚁要从点 $P$ 爬到点 $B$ ，它的最短行程是（）米

A、5 B、 $\sqrt{18}$ C、 $\sqrt{13}$ D、3

查看试题解析
11. 如图，长方体的所有棱长和为 $48 c m$ ，长、宽、高的比为 $3 ： 2 ： 1$ ，若一只蚂蚁从顶点 $A$ 沿长方体表面爬行到顶点 $B$ ，从点 $A$ 爬行到点 $B$ 的最短路程是（） $c m$ ．

A、 $2 \sqrt{26}$ B、 $4 \sqrt{5}$ C、 $6 \sqrt{2}$ D、 $12$

查看试题解析
12. 为迎接新年的到来，同学们做了许多拉花布置教室，准备召开新年晚会，小刘搬来一架高2.5米的木梯，准备把拉花挂到2.4米高的墙上，则梯脚与墙角距离应为（）

A、0.7米 B、0.8米 C、0.9米 D、1.0米

查看试题解析
13. 如图，圆柱形玻璃杯高为 $14 cm$ ，底面周长为 $32 cm$ ，在杯内壁离杯底 $5 cm$ 的点 $B$ 处有一滴蜂蜜（杯壁厚度不计），此时一只蚂蚁正好在杯外壁，离杯上沿 $3 cm$ 与蜂蜜相对的点 $A$ 处，则蚂蚁从外壁 $A$ 处到内壁 $B$ 处的最短距离为（）

A、 $20 cm$ B、 $16 cm$ C、 $22 cm$ D、 $27 cm$

查看试题解析
14. 如图，有一个高为8cm ，底面周长为6 cm的圆柱形容器，在外壁距下沿3c m的点A处有一只蚂蚁，与蚂蚁相对的内壁距上沿4 cm 的点 B 处有一滴蜂蜜，则蚂蚁从A 处到蜂蜜 B 处所走的最短路径长为.

查看试题解析
15. 如图，是一个四级台阶，它的每一级的长、宽和高分别为5，1.5 和1.5，A 和 B 是这个台阶的两个相对的端点，B点上有一只蚂蚁，想到A点去觅食，则蚂蚁从 B 点出发，沿着台阶面爬到A点，最短路径长为.

查看试题解析
16. 如图，在棱长为2 的正方体中，蚂蚁从正方体下方一边 AB 的中点 P 出发爬到顶点( $C^{'}$ 处，若蚂蚁选择的路径是最短的，则最短路径长为.

查看试题解析
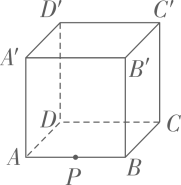17. “中华人民共和国道路交通管理条例”规定：小汽车在城市街道上的行驶速度不得超过70千米/时．一辆“小汽车”在一条城市街路上直道行驶，某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处，过了6秒后，测得“小汽车”位置B与“车速检测仪A”之间的距离为130米，这辆“小汽车”超速了吗？请说明理由．

查看试题解析
18. 小明为了测量池塘两端C，D的距离，想了如下办法：在平地上寻找到两点A，B，测得 $A B = B C = 5 m, A D = 10 m, ∠ B = 90 °, ∠ B A D = 135 °$ ．请你帮小明求出C，D两点的距离．

查看试题解析

三、综合拓展

19. 著名的赵爽弦图（如图1），其中四个直角三角形较大的直角边长都为 $a$ ，较小的直角边长都为 $b$ ，斜边长都为 $c$ ，大正方形的面积可以表示为 $c^{2}$ ，也可以表示为 $4 \times \frac{1}{2} a b + {(a - b)}^{2}$ ，由此推导出重要的勾股定理：如果直角三角形两条直角边长为 $a$ ， $b$ ，斜边长为 $c$ ，则 $a^{2} + b^{2} = c^{2}$ .

(1)、在图2中，四边形 $A C F E$ 是正方形，利用两种不同的方法表示出四边形 $A B E D$ 的面积，也可以证明勾股定理，请你利用图2推导勾股定理；

(2)、如图3，在一条东西走向河流的一侧有一村庄 $C$ ，河边原有两个取水点 $A$ 、 $B$ ， $A B = A C$ ，由于某种原因，由 $C$ 到 $A$ 的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点 $H$ （ $A$ 、 $H$ 、 $B$ 在同一条直线上），并新修一条路 $C H$ ，且 $C H ⊥ A B$ .测得 $C H = 1.2$ 千米， $H B = 0.8$ 千米，求新路 $C H$ 比原路 $C A$ 少多少千米？

(3)、在第（2）问中，若 $A B \neq A C$ ，如图4， $C H ⊥ A B$ ， $A C = 1$ 千米， $B C = 1.7$ 千米， $A B = 2.1$ 千米，求 $C H$ 的长.

查看试题解析
20. 阅读下列材料并完成任务：“最短路径问题”是数学中一类具有挑战性的问题．其实，数学史上也有不少相关的故事，如下即为其中较为经典的一则：古希腊有一位久负盛名的学者，名叫海伦．他精通数学，物理，聪慧过人．有一天，一位将军向他请教一个问题：如图1，将军从甲地骑马出发，要到河边让马饮水，然后再回到乙地的马棚，为使马走的路程最短，应该让马在什么地方饮水？海伦认为以河边为镜面，画出甲地的镜像点(垂直河边的等距离点)，然后连接乙地和甲地的镜像点，会跟河边相交一点，这个点就是马饮水的地方，马走的路程最短(两点之间直线距离最短)．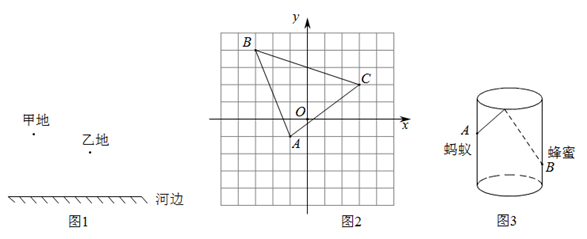

任务：

(1)、请你帮海伦在图1的位置完成作图，并标出马饮水的地点P（画出草图即可）；

(2)、如图2， $△$ ABC的三个顶点的坐标分别为A(-1，-1)，B(-3，4)，C(3，2)．请你在x轴上找一点Q ，使得QB+QC最小（保留作图痕迹）；

(3)、应用：
如图3，圆柱形容器高为18cm，底面周长为24cm．在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm处的点A处，点A与B的水平距离等干底面直径，求蚂蚁从外壁A处到达内壁B处的最短距离．

查看试题解析