1.3 《勾股定理的应用》（1）—北师大版数学八年级上册课堂分层训练

试卷更新日期：2025-08-11 类型：同步测试

进入出卷网下载

一、基础应用

1. 一架长 $5 m$ 的梯子，如图那样斜靠在一面墙上，梯子的底端离墙 $1.4 m$ ，如果梯子的顶端下滑 $0.8 m$ ，那么他的底部滑行了（）

A、 $0.8 m$ B、 $1 m$ C、 $1.2 m$ D、 $1.6 m$

查看试题解析
2. 如图，一根垂直于地面的旗杆在离地面面 $5 m$ 处折断，旗杆顶部落在离旗杆底部 $12 m$ 处，旗杆折断之前的高度是（）

A、 $5 m$ B、 $12 m$ C、 $13 m$ D、 $18 m$

查看试题解析
3. 一个台阶如图，阶梯每一层高 $15 cm$ ，宽 $25 cm$ ，长 $60 cm$ ．一只蚂蚁从 $A$ 点爬到 $B$ 点最短路程是（）

A、 $60 cm$ B、 $80 cm$ C、 $90 cm$ D、 $100 cm$

查看试题解析
4. 如图，一条小巷的左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙脚的距离 $O B$ 为1.5米，梯子顶端到地面距离 $A B$ 为2米．若梯子底端位置保持不动，将梯子斜靠在右墙时，梯子顶端到地面距离 $C D$ 为2.4米，则小巷的宽度 $B D$ 为（）

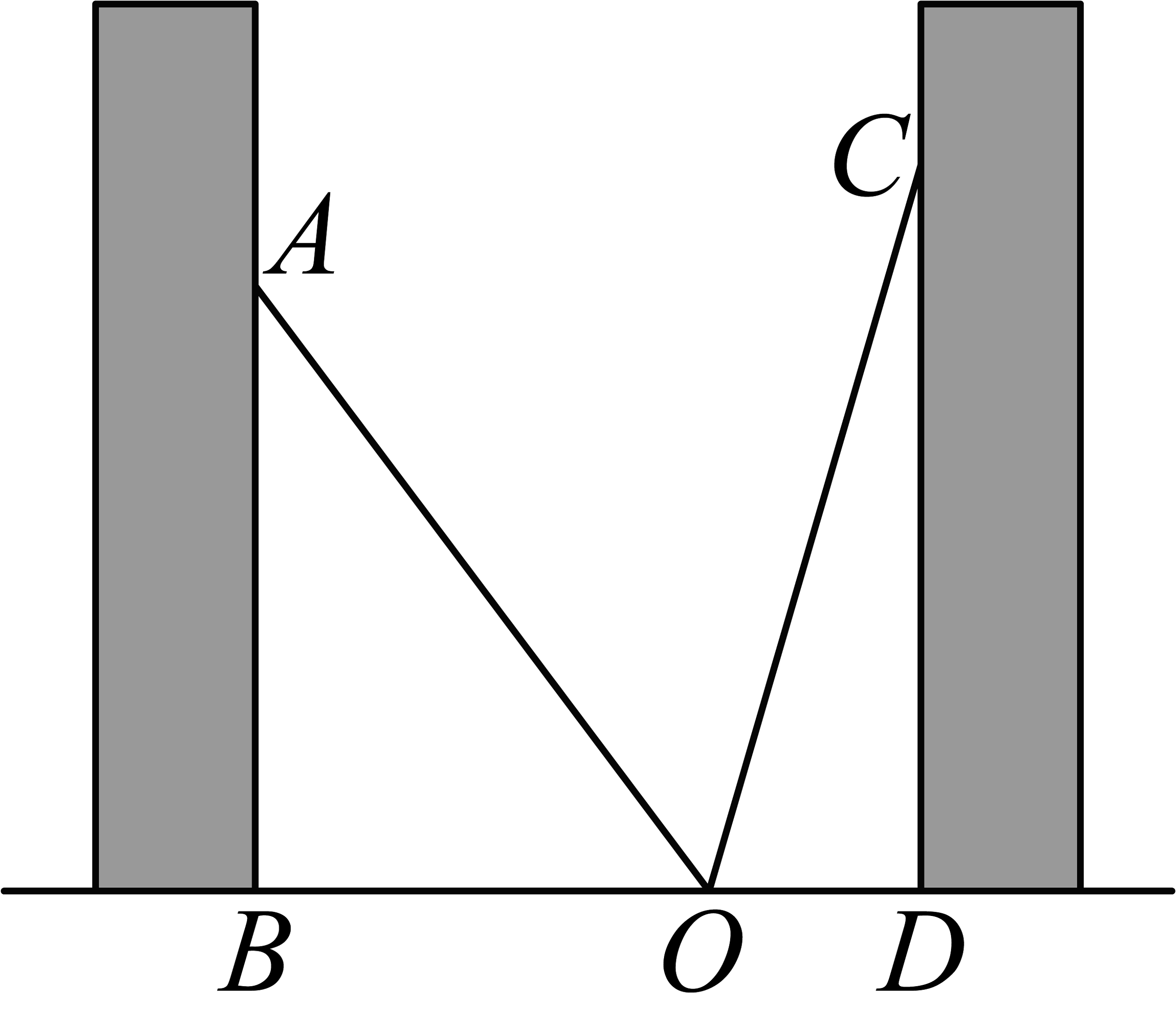A、2.2米 B、2.3米 C、2.4米 D、2.5米

查看试题解析
5. 如图所示，是一块由花园小道围成的边长为12米的正方形绿地，在离 $C$ 处5米的绿地旁边 $B$ 处有健身器材，为保护绿地，不直接穿过绿地从 $A$ 到 $B$ ，而是沿小道从 $A \to C \to B$ ，这样多走了米．

查看试题解析
6. 如图，一个游泳爱好者，要横跨一条宽 $A C = 8 m$ 的河流，由于水流速度的原因，这位游泳爱好者向下游偏离了 $B C = 6 m$ ，这位游泳爱好者在横跨河流时的实际游泳距离为米．

查看试题解析
7. 为了更好地提升居民的生活水平和居住满意度，某小区进行小范围绿化，要在一块如图所示的四边形空地ABCD内进行绿化改造，∠A＝90°，AB＝12m ， AD＝9m ， BC＝17m ， CD＝8m ．

(1)、若要在B ， D两点间铺一条鹅卵石路，铺设成本为120元/m；最低花费为多少元？

(2)、如果种植草皮的费用是200元/m² ，那么在整块空地上种植草皮共需投入多少元？

查看试题解析

二、能力提升

8. 如图，铁路MN和公路PQ在点O处交汇，∠QON＝30°．公路PQ上A处距O点240米．如果火车行驶时，周围200米以内会受到噪音的影响．那么火车在铁路MN上沿ON方向以20米/秒的速度行驶时，A处受噪音影响的时间为（　　）

A、16秒 B、18秒 C、20秒 D、22秒

查看试题解析
9. 如图，有一个绳索拉直的木马秋干，绳索AB的长度为5米，若将它往水平方向向前推进3米（即DE=3米），且绳索保持拉直的状态，则此时木马上升的高度为（）

A、1米 B、 $\sqrt{2}$ 米 C、2米 D、4米

查看试题解析
10. 我国古代数学著作《九章算术》记载了一道有趣的问题．原文是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何．译为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度与这根芦苇的长度分别是多少？设芦苇的长度是x尺．根据题意，可列方程为（）

A、（x﹣1）²+5²＝x² B、x²+10²＝（x+1）² C、（x﹣1）²+10²＝x² D、x²+5²＝（x+1）²

查看试题解析
11. 如图， $E$ 为矩形 $A B C D$ 的边 $A B$ 上一点，将矩形沿 $C E$ 折叠，使点 $B$ 恰好落在 $E D$ 上的点 $F$ 处．若 $B E = 1 ， B C = 3$ ，则 $C D$ 的长为（）

A、6 B、5 C、4 D、3

查看试题解析
12. 如图，在矩形纸片 $A B C D$ 中， $A D = 8$ ，折叠纸片，使 $A B$ 边与对角线 $A C$ 重合，点 $B$ 落在点 $F$ 处，折痕为 $A E$ ，若 $E F = 3$ ，则 $A B$ 的长为.

查看试题解析
13. 如图，在矩形 $A B$ $C D$ 中， $C D = 4 ， B C = 8$ ，将 $△ B C D$ 沿 $B D$ 翻折得到 $△ B E D ， B E$ 交 $A D$ 于点 $F$ ，则 $A F =$

查看试题解析
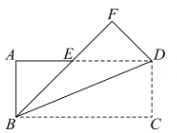14. 2025年1月1日，汕头市区春节烟火晚会精彩呈现，吸引了近万名市民共同感受“粤东之城，蛇年呈祥”的美好图景．如图，东海岸道路上有A、B两个出口，相距250米，在公路北面不远处的C地是烟火晚会烟花燃放处，已知C与A的距离为150米，与B的距离为200米，在烟花燃放过程中，为了安全起见，燃放点C周围半径130米范围内不得进入．

(1)、烟花燃放点C距离公路的垂直距离为多少米？

(2)、烟花燃放过程中，按照安全要求，A、B之间的公路是否需要暂时封锁？若需要封锁，请说明理由，并求出需要封锁的公路长．

查看试题解析
15. 如图，某沿海城市A接到台风预警，在该市正南方向 $340 km$ 的B处有一台风中心，沿 $B C$ 方向以 $20 km/h$ 的速度移动，已知城市A到 $B C$ 的距离 $A D$ 为 $160 km$ ．

(1)、台风中心经过多长时间从B点移到D点？

(2)、如果在距台风中心 $200 km$ 的圆形区域内都将受到台风的影响，那么A市受到台风影响的时间持续多少小时？

查看试题解析
16. 如图，有一架秋千，当它静止时，踏板离地的垂直高度 $D E = 1 m$ ，将它往前推送 $4 m$ （水平距离 $B C = 4 m$ ）时，秋千的踏板离地的垂直高度 $B F = 2 m$ ，秋千的绳索始终拉得很直，求绳索 $A D$ 的长度．

查看试题解析

三、综合拓展

17.

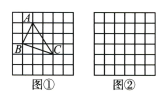
(1)、问题背景
在△ABC 中，AB，BC，AC 三边的长分别为 $\sqrt{5} ， \sqrt{10} ， \sqrt{13} ，$ 求这个三角形的面积.小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC(即△ABC 三个顶点都在小正方形的顶点处)，如图①所示.这样不需求△ABC 的高，而借用网格就能计算出它的面积.
请你将△ABC 的面积直接填写在横线上：.

(2)、思维拓展
我们把上述求△ABC 面积的方法叫作构图法，若△ABC 三边的长分别为 $\sqrt{5} a ， 2 \sqrt{2} a ， \sqrt{17} a (a⟩ 0) ，$ 请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC，并求出它的面积.

(3)、探索创新
若△ABC三边的长分别为 $\sqrt{m^{2} + 16 n^{2}} ， \sqrt{9 m^{2} + 4 n^{2}} ，$ $2 \sqrt{m^{2} + n^{2}} (m⟩ 0 ， n > 0 ，$ 且m≠n)，试运用构图法求出这个三角形的面积.

查看试题解析

18. 阅读与思考

阅读下列材料并完成相应的任务．

我国是最早了解和应用勾股定理的国家之一，古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用，古希腊数学家毕达哥拉斯首先证明了勾股定理，在西方，勾股定理又称为“毕达哥拉斯定理”．关于勾股定理的研究还有一个很重要的内容是勾股数组，在课本中我们已经了解到“能够成为直角三角形三条边的三个正整数称为勾股数”．

以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：

方法1：若m为奇数 $(m \geq 3)$ ，则 $a = m$ ， $b = \frac{1}{2} (m^{2} - 1)$ 和 $c = \frac{1}{2} (m^{2} + 1)$ 是勾股数．

方法2：若任取两个正整数m和 $n (m > n)$ ，则 $a = m^{2} - n^{2}$ ， $b = 2 m n$ ， $c = m^{2} + n^{2}$ 是勾股数．

任务：

(1)、在以上两种方法中任选一种，证明以a，b，c为边长的

△ A B C

是直角三角形．

(2)、学校园林设计师按照如图所示的方式摆放兰花，已知这四个直角三角形全等，且直角三角形的三边是勾股数，较短的直角边长为

7 m

，要求在每个直角三角形的三个顶点处需要摆放一盆兰花，每个直角三角形的三条边间隔1米摆放一盆兰花，请你计算出总共需要的兰花数量．

查看试题解析