人教版七上数学第二章《有理数的运算》——实践与探究类专项：基础应用篇+思维进阶篇

试卷更新日期：2025-08-07 类型：复习试卷

进入出卷网下载

一、基础应用

1. 根据以下素材，尝试解决问题.

如何获得更高的销售额?
素材1	甲菜农有6筐蔬菜，每筐质量在20千克左右，他将超过20千克的千克数记为正数，不足的千克数记为负数，记录如图.超过20千克的他以170元/筐的价格售出，其余三筐他以9元/千克销售，并全部售出.
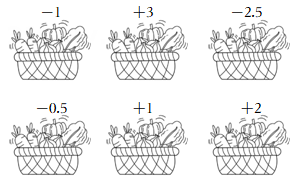
素材2	乙菜农将蔬菜堆放在一起进行销售，售出蔬菜的质量比甲菜农少20千克，其中80千克以10 元/千克销售，剩下的部分按八折全部售出.
问题解决
问题1	(1)求甲菜农售出最重的一筐蔬菜的质量.
问题2	(2)求乙菜农售出的蔬菜的总质量.
问题3	(3)甲、乙菜农的蔬菜全部售出后，哪一位菜农的销售额更高? 高多少元?

查看试题解析

2. 根据下列素材，探索完成任务：

哪种计算工资方式对工人更有利？

素材 1

玩具厂定额每个工人每天生产玩具车20辆，某工人每天生产的玩具车数量与计划定额有出入，如表是该工人某周每天生产的情况(以20辆为标准，超产记为正，减产记为负)

时间	星期一	星期二	星期三	星期四	星期五	星期六	星期天
数量(辆)	$- 2$	$+ 4$	$+ 4$	$+ 6$	$0$	$- 5$	$+ 3$

素材 2

该工厂计算工资有两种方式：

方式A：每生产一辆玩具车报酬为10元；

方式B：实行日计件工资制，每生产一辆报酬9元。

若一天超出定额20辆，则超过部分另外加12元/辆。

若一天不足定额20辆，则根据不足数量扣5元/辆。

问题解决

任务 1

本周该工人最多一天比最少一天多生产 ▲ 辆玩具车。

任务 2

本周该工人实际生产玩具车多少辆？

任务 3

请判断哪种计算工资的方式对该工人更有利，通过计算说明。

查看试题解析

3. 素材1：每年秋天是灵昆柿子饼盛产期．小黄同学打算从灵昆寄5袋柿子饼到杭州，以每袋3千克为标准，超过的千克数记为正数，不足的千克数记为负数，记录如下表所示：
柿子饼袋
①
②
③
④
⑤
与标准重量的差值（单位：千克）
0.1
-0.3
0
-0.1
0.2
素材2：小黄同学选择了某快递，收费标准如下：3千克以内15元（含3千克），超过1千克的部分为2元/每千克（不足1千克按1千克计）．现该快递公司提供多种寄件方式：
纸箱类型
中型纸箱
大型纸箱
可容纳袋数（袋/个）
2
4
重量（千克/个）
0.4
0.7
价格（元/个）
3
5
方案一：小黄购买了中型纸箱将重量最低的②、④柿子饼袋打包在一起，其余每小袋各自寄出．
方案二：____．

(1)、【任务1】求这5袋柿子饼的总重量．

(2)、【任务2】求方案一所需要的费用．

(3)、【任务3】请你设计方案二，使它的费用低于方案一，并计算你的方案费用．

查看试题解析

4. 根据背景素材，探索解决问题．

周末小明打算去露营基地野餐
素材1	路线图：家→炸鸡店→面包店→水果店→奶茶店→露营基地；
素材2	这条路线近似看成东西走向.如果规定向东为正，向西为负，他这天行车里程（单位：km）如下：-3，+5，+2，-4，-1；
素材3	滴滴车价目表：起步价（不超过3km时）车费8元，超过3km时，每千米车费加价2元，消费满10元赠送一张8折优惠券和一张7折优惠券（每种优惠券只能使用一次）．
问题解决
任务1	求露营基地在家的哪个方向，并求出与家的距离；
任务2	计算炸鸡店到面包店所用的车费；
任务3	该路线如何正确使用优惠券，使总车费最低，求最低总车费．

查看试题解析

5. 根据以下素材，探索完成任务．

如何规划游玩路线？
素材1	温州轨道交通实行里程分段计价票制，起步价 $2$ 元，可乘坐 $4 k m$ （含 $4 k m$ ）， $4$ 至 $28 k m$ （含 $28 k m$ ）每 $1$ 元可乘 $4 k m$ （不足 $4 k m$ 按 $1$ 元算）．如：桐岭站到动车南站共 $5.3 k m$ ，收费 $3$ 元．部分站点距离见下图（单位： $k m$ ）
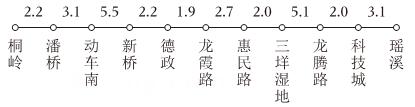
素材2	一名成年乘客可免费携带一名身高不足 $1.2$ 米（含 $1.2$ 米）的儿童乘车．
素材3	小明一家四口将乘坐轻轨出游．小明家住在新桥站附近，家庭成员如下：小明（身高 $1.5$ 米）、弟弟（身高 $1.1$ 米）、爸爸、妈妈．
问题解决
分析规划	任务1	从新桥站到桐岭站为 ▲ $k m$ ，单人单程乘坐需车费 ▲ 元．
	任务2	小明一家乘坐轻轨从新桥站到三垟湿地站，需要多少车费．
确定方案	任务3	小明一家从新桥站出发，计划共用 $30$ 元车费出行（往返），请你为小明一家规划一个尽可能远的游玩站点，并说明理由．

查看试题解析

二、思维进阶

6. 【综合与实践】小明和小红假期到某厂参加社会实践，发现该厂用一批长为12 cm，宽为8 cm的白纸板做无盖包装盒（不考虑连接的重叠部分）。制作时，工厂一般将白纸板分隔成两个长方形分别制作底面和侧面，截得底面后的剩余部分不再使用，请根据活动完成相应的任务。

(1)、【活动一】如图1是常见的一种设计方案甲：在白纸板上截去两部分（图中阴影部分），盒子底面的四边形ABCD是正方形，然后沿虚线折成一个无盖的长方体包装盒。
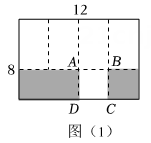
[任务1]：请计算方案甲中包装盒的容积；

(2)、【活动二】为了增加包装盒的容积，有人提议将包装盒设计成圆柱形。小明横着裁剪把长方形的长作为底面圆的周长进行设计，得到如图2的方案乙。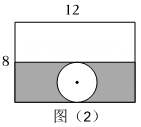
[任务2]：请计算方案乙中无盖圆柱形包装盒的容积，并判断容积是否变大；（π取3）

(3)、【活动三】小明：设计成圆柱形的容积确实变化了。
小红：那么是否还有容积更大的情况呢？
小明与小红通过研究发现了无盖圆柱形包装盒设计的新方案，且容积还大于50cm³。
[任务3]：请在下列白纸板上画出他们的方案，并计算其容积。（π取3）

查看试题解析
7. 十几年前我国曾经流行一种叫“二十四点”的数学趣味算题，方法是给出1~13之间的自然数，从中任取四个，将这四个数(四个数都只能用一次)进行“+”“-”“×”“ ÷”运算，可加括号使其结果等于24．
例如：对1，2，3，4可运算(1+2+3)×4=24，也可以写成4×(1+2+3)=24，但视作相同的方法．
现在郑、付两名同学的手中分别握着四张扑克牌(见下图)；若红桃♥、方块◆上的点数记为负数，黑桃♠、梅花♣，上的点数记为正数．
请你对郑、付两名同学的扑克牌按要求进行记数，并按前面“二十四点”运算方式对郑、付两名同学的记数分别进行列式计算，使其运算结果均为24．(分别尽可能提供多种算法)
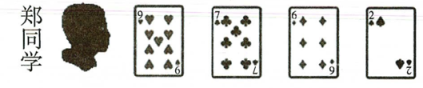
依次记为：，，，。
依次记为：，，，。
⑴帮助郑同学列式计算：
⑵帮助付同学列式计算：

查看试题解析

柿子饼袋	①	②	③	④	⑤
与标准重量的差值（单位：千克）	0.1	-0.3	0	-0.1	0.2

纸箱类型	中型纸箱	大型纸箱
可容纳袋数（袋/个）	2	4
重量（千克/个）	0.4	0.7
价格（元/个）	3	5