湘教版（2024）数学八年级上册课时训练1.2提公因式法第二课时

试卷更新日期：2025-08-06 类型：同步测试

进入出卷网下载

1. 把多项式(1+x)(1-x)-(x-1)提取公因式(x-1)后，余下的部分是（）

A、(x+1) B、-(x+1) C、x D、-(x+2)

查看试题解析
2. 把多项式（m+1）（m﹣1）+（m﹣1）提取公因式（m﹣1）后，余下的部分是（　　）

A、m+1 B、2m C、2 D、m+2

查看试题解析
3. 分解因式b²（x﹣3）+b（x﹣3）的正确结果是（　　）

A、（x﹣3）（b²+b） B、b（x﹣3）（b+1） C、（x﹣3）（b²﹣b） D、b（x﹣3）（b﹣1）

查看试题解析
4. 因式分解：2a(x-y)+3b(y-x)正确的是（）

A、(x-y)(2a-3b) B、(x+y)(2a-3b) C、(y-x)(2a+3b) D、(x+y)(2a+3b)

查看试题解析
5. 下列各式中，没有公因式的是（）

A、3x﹣2与6x²﹣4x B、ab﹣ac与ab﹣bc C、2（a﹣b）²与3（b﹣a）³ D、mx﹣my与ny﹣nx

查看试题解析
6. 已知（2x-21）（3x-7）-（3x-7）（x-13）可分解因式为（3x+a）（x+b）其中a，b均为整数，则a+3b=（）

A、30 B、 C、31 D、

查看试题解析
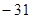7. 多项式x²y（a-b）-xy（b-a）+y（a-b）提公因式后，另一个因式为（　　）

A、 $x^{2} - x + 1$ B、 $x^{2} + x + 1$ C、 $x^{2} - x - 1$ D、 $x^{2} + x - 1$

查看试题解析
8. 把多项式a²(x-5)²-a(5-x)分解因式正确的是（）

A、a(x-5)(ax-5a+1) B、a(5-x)(ax-5a+1) C、a(x-5)(ax-5a-1) D、a(x-5)(ax+5a+1)

查看试题解析

9. 整式 $a ^{2} - a$ 和 $(a - 1) ^{2}$ 的公因式为.

查看试题解析
10. 因式分解： ${(a - b)}^{2} - (b - a) =$ ；

查看试题解析
11. 分解因式，直接写出结果 $8 a (x - a) + 4 b (a - x) - 6 c (x - a)$ =

查看试题解析
12. 化简代数式 $（ x - 3 ）（ x - 4 ） - （ x - 1 ）（ x - 3 ）$ ，结果是.

查看试题解析
13. 多项式 $a (a - b - c) + b (c - a + b) + c (b + c - a)$ 提出公因式 $a - b - c$ 后，另外一个因式为

查看试题解析

17. 已知（10x-31）（13x-17）-（13x-17）（3x-23）可因式分解成（ax+b）（7x+c），其中a、b、c均为整数，求a+b+c的值

查看试题解析
18.
先化简，在求值：30x $2$ (y+4)-15x(y+4)，其中x=2，y=-2

查看试题解析